Trắc nghiệm Ôn tập chương II Hình học có đáp án (Vận dụng)
-
1808 lượt thi
-
10 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 3:
Điền từ thích hợp vào chỗ trống
Cho △ABC = △MNP.
Biết AB + BC = 7cm, MN – NP =3cm, MP =4cm.
Chu vi tam giác ABC là: ____(cm)
 Xem đáp án
Xem đáp án
Ta có: △ABC = △MNP
⇒ AB = MN, BC = NP, AC = MP (các cặp cạnh tương ứng)
Mà MN – NP =3cm ⇒ AB – BC =3cm
Theo bài có AB + BC =7cm
Suy ra: 2AB =10cm ⇒ AB =5cm
⇒ BC =7 – AC =2cm
Do đó ta có: AB = 5cm, BC = 2cm, AC =4cm
Vậy chu vi tam giác ABC bằng:
AB + BC + AC = 5 + 2 + 4 =11cm
Đáp án cần điền vào ô trống là: 11
Câu 5:
Lựa chọn đúng hay sai
1. Nếu hai tam giác bằng nhau thì hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia.
2. Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
3. Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai cạnh còn lại cũng bằng nhau.
4. Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai cặp góc còn lại cũng tương ứng bằng nhau.
5. Nếu hai tam giác có hai cặp góc tương ứng bằng nhau thì hai tam giác cũng có hai cặp cạnh tương ứng bằng nhau.
 Xem đáp án
Xem đáp án
Ý thứ 1: 1-Đúng. Vì theo định nghĩa hai tam giác bằng nhau.
Ý thứ 2: 2- Đúng vì theo trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác
Ý thứ 3: 3- Đúng vì theo trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, ta có hai tam giác bằng nhau nên hai cạnh còn lại bằng nhau
Ý thứ 4: 4- Đúng vì theo trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, ta có hai tam giác bằng nhau nên hai cặp góc tương ứng còn lại bằng nhau
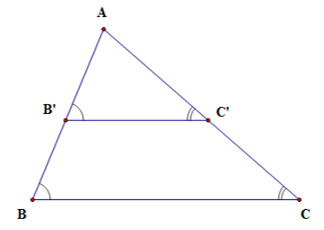
Ý thứ 5: 5- Sai, ví dụ hai tam giác ABC và A′B′C′ có nhưng không có hai cặp cạnh nào bằng nhau
Câu 7:
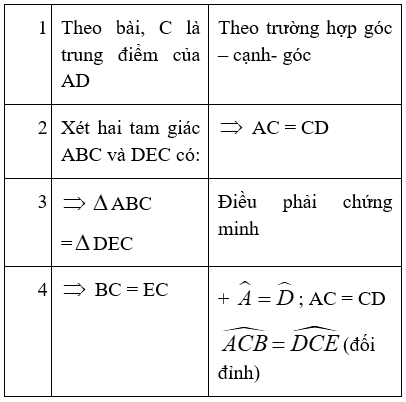
Nối từ hoặc cụm từ ở cột bên trái với cột bên phải để được câu hoàn chỉnh
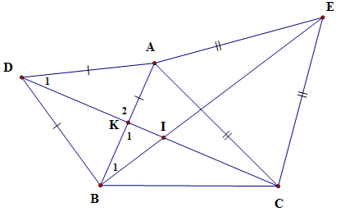
(Biết rằng C là trung điểm của AD và
Hãy nối các ý với nhau để được một bài chứng minh BC = EC)
 Xem đáp án
Xem đáp án
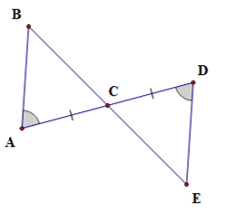
Bài chứng minh hoàn chỉnh như sau:
Theo bài: C là trung điểm của AD
⇒AC = CD
Xét hai tam giác ABC và DEC có:
+
+ AC = CD
+ (đối đỉnh)
⇒△ABC = △DEC ( g- c - g)
⇒BC = EC (đpcm)