Trắc nghiệm Toán 7 CD Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Phần 2) có đáp án
Trắc nghiệm Toán 7 CD Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Nhận biết) có đáp án
-
487 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Cho tam giác ABC và tam giác MNP có ; AB = PN, AC = PM. Phát biểu nào sau đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét ∆ABC và ∆MNP có:
AB = PN
AC = PM
Suy ra ∆ABC = ∆PNM (c.g.c)
(Trong đó:
Đỉnh A tương ứng với đỉnh P.
Đỉnh B tương ứng với đỉnh N.
Đỉnh C tương ứng với đỉnh M).
Câu 3:
Cho tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN. Cần thêm điều kiện gì để ∆ABC = ∆MNP theo trường hợp hai cạnh góc vuông?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN.
Nên để ∆ABC = ∆MNP theo trường hợp hai cạnh góc vuông cần thêm điều kiện BC = NP. (Do AB, BC là hai cạnh góc vuông của tam giác ABC; AN, NP là hai cạnh góc vuông của tam giác MNP).
Câu 4:
Cho tam giác ABC và tam giác NPM có BC = PM; . Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì tam giác ABC và tam giác NPM có BC = PM; .
Nên để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh cần thêm điều kiện AC = NM. (Do 
là góc xen giữa hai cạnh BC và AC; là góc xen giữa hai cạnh PM và NM).
Câu 5:
Cho hình sau, cần thêm điều kiện gì để ∆ACP = ∆ABN theo trường hợp cạnh- góc- cạnh
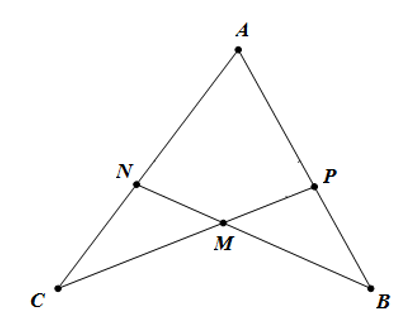
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆ACP và ∆ABN có
là góc chung
Mà góc A là góc xen giữa hai cạnh AC và AP của ∆ACP; góc A là góc xen giữa hai cạnh AB và AN của ∆ABN.
∆ACP = ∆ABN thì cạnh AC = AB và AP = AN (các cạnh tương ứng)
Vậy cần thêm điều kiện AC = AB và AP = AN thì ∆ACP = ∆ABN theo trường hợp cạnh- góc- cạnh.