Dạng 2. Cách viết giả thiết, kết luận, vẽ hình và chứng minh một định lí có đáp án
-
848 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau”.
Viết giả thiết, kết luận của định lí trên;
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
|
GT |
aa' cắt cc’ tại A; bb' cắt cc’ tại B; \[\widehat {aAB} = \widehat {ABb'}\] |
|
KL |
\[\widehat {cAa'} = \widehat {ABb'}\] \[\widehat {aAB} = \widehat {bBc'}\] \[\widehat {aAc} = \widehat {bBA}\] \[\widehat {a'AB} = \widehat {b'Bc'}\] |
Câu 2:
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau”.
Vẽ hình;
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
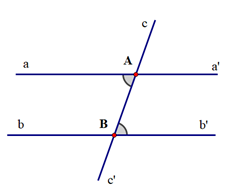
Câu 3:
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau”.
Chứng minh định lí.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
+ Ta có \[\widehat {aAB} = \widehat {ABb'}\] (giả thiết)
Mà \[\widehat {aAB} = \widehat {cAa'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {cAa'} = \widehat {ABb'}\] (vì cùng bằng \[\widehat {aAB}\]).
+ Ta có \[\widehat {aAB} = \widehat {ABb'}\](giả thiết)
Mà \[\widehat {ABb'} = \widehat {bBc'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {aAB} = \widehat {bBc'}\] (vì cùng bằng \[\widehat {ABb'}\]).
+ Ta có \[\widehat {aAc}\] + \[\widehat {BAa}\] = 180° (hai góc kề bù)
Và \[\widehat {bBA}\] + \[\widehat {ABb'}\] = 180° (hai góc kề bù)
Mà \[\widehat {aAB} = \widehat {ABb'}\]
Suy ra \[\widehat {aAc}\] = \[\widehat {bBA}\].
+ Ta có \[\widehat {a'AB}\] = \[\widehat {aAc}\] (hai góc đối đỉnh)
\[\widehat {b'Bc'}\] = \[\widehat {bBA}\] (hai góc đối đỉnh)
Mà \[\widehat {aAc}\] = \[\widehat {bBA}\]
Suy ra \[\widehat {a'AB} = \widehat {b'Bc'}\].
Vậy định lí được chứng minh.
Câu 4:
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau”.
Viết giả thiết, kết luận của định lí trên;
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
|
GT |
aa' cắt cc’ tại A; bb' cắt cc’ tại B; aa’ // bb’ |
|
KL |
\[\widehat {aAB} + \widehat {ABb} = 180^\circ ;\] \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ \] |
Câu 5:
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau”.
Vẽ hình cho định lí trên;
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
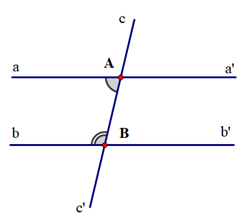
Câu 6:
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau”.
Chứng minh định lí.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
+ Ta có aa’ // bb’ (giả thiết) nên \[\widehat {aAB} = \widehat {ABb'}\] (hai góc so le trong)
Vì \[\widehat {ABb}\] và \[\widehat {ABb'}\] là hai góc kề bù nên \[\widehat {ABb} + \widehat {ABb'} = 180^\circ \]
Suy ra \[\widehat {ABb} + \widehat {aAB} = 180^\circ \]
+ Ta có aa’ // bb’ (giả thiết) nên \[\widehat {a'AB} = \widehat {ABb}\] (hai góc so le trong)
Mà \[\widehat {ABb} + \widehat {ABb'} = 180^\circ \] (chứng minh trên)
Suy ra \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ \]
Vậy định lí được chứng minh.
Câu 7:
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Giả thiết và kết luận của định lí trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Giả thiết là: một đường thẳng vuông góc với một trong hai đường thẳng song song.
Kết luận là: đường thẳng đó vuông góc với đường thẳng còn lại.
Ta có thể viết giả thiết và kết luận của định lí trên bằng kí hiệu như sau:
|
GT |
x \( \bot \) y; y // z |
|
KL |
x \( \bot \) z |
Câu 8:
Phát biểu định lí sau bằng lời:
|
GT |
a // b; c // b; a ≠ c |
|
KL |
a // c |
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Bảng trên được phát biểu như sau: Nếu hai đường thẳng a và c (khác a) cùng song song với đường thẳng b thì a // c.
Một cách tổng quát ta có định lí: Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 9:
Phát biểu định lí sau bằng lời:
|
GT |
a ⊥ b; c ⊥ b; a ≠ c |
|
KL |
a // c |
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Bảng trên được phát biểu như sau: Nếu hai đường thẳng a và c (khác a) cùng vuông góc với đường thẳng b thì a // c.
Một cách tổng quát ta có định lí: Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 10:
Cho định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc trong cùng phía bù nhau” và hình vẽ minh hoạ sau:
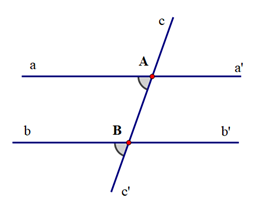
Hãy viết giả thiết, kết luận cho định lý trên:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Giả thiết, kết luận của định lý trên là:
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb' \[\widehat {aAB} = \widehat {bBc'}\] |
|
KL |
\[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
Câu 11:
Cho hình vẽ:
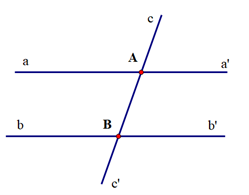
Bảng sau là giả thiết, kết luận của định lí nào?
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B (aa' ≠ bb') \[\widehat {aAB}\] + \[\widehat {ABb}\] = 180° |
|
KL |
\[\widehat {aAB} = \widehat {ABb'};\]\[\widehat {a'AB} = \widehat {ABb}\] |
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Định lí: “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì các cặp góc so le trong bằng nhau” có giả thiết, kết luận được xác định như trên.
Câu 12:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra từ: “Nếu hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”.
Thật vậy ta có thể chứng minh định lí như sau:
|
GT |
a ⊥ c; b ⊥ c; a ≠ b |
|
KL |
a // b |
Chứng minh (hình vẽ dưới đây):
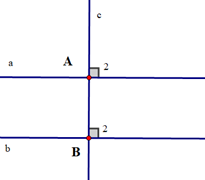
Ta có a ⊥ c (giả thiết) suy ra \({\widehat A_2} = {90^o}\);
b ⊥ c (giả thiết) suy ra \({\widehat B_2} = {90^o}\)
Suy \({\widehat A_2} = {\widehat B_2}\left( { = 90^\circ } \right)\)
Mà \({\widehat A_2}\) và \({\widehat B_2}\) là hai góc ở vị trí đồng vị
Suy ra a // b (dấu hiệu nhận biết)
Vậy định lí được chứng minh.
Câu 13:
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
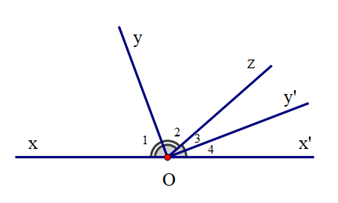
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra Oy vuông góc với Oy'
Vậy định lí được chứng minh.”;
(II). “Vì Oy' là tia phân giác của \(\widehat {x'Oz}\) (giả thiết) nên \({\widehat O_3} = \frac{1}{2}\widehat {x'Oz}\)”;
(III) “Mà \(\widehat {xOz}\) và \(\widehat {zOx'}\)là hai góc kề bù (giả thiết)
Nên \(\widehat {xOz} + \widehat {zOx'} = 180^\circ \) (tính chất hai góc kề bù)
Do đó \(\widehat {yOy'} = \frac{1}{2}{.180^o} = {90^o}\)”;
(IV). “Có \(\widehat {yOy'} = {\widehat O_2} + {\widehat O_3}\)\( = \frac{1}{2}\widehat {xOz} + \frac{1}{2}\widehat {x'Oz}\)\( = \frac{1}{2}\left( {\widehat {xOz} + \widehat {zOx'}} \right)\)”
(V). “Vì Oy là tia phân giác của \(\widehat {xOz}\)(giả thiết) nên \({\widehat O_2} = \frac{1}{2}\widehat {xOz}\)”.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Để chứng minh định lí trên, ta làm như sau:
Vì Oy là tia phân giác của \(\widehat {xOz}\)(giả thiết) nên \({\widehat O_2} = \frac{1}{2}\widehat {xOz}\)
Vì Oy' là tia phân giác của \(\widehat {x'Oz}\) (giả thiết) nên \({\widehat O_3} = \frac{1}{2}\widehat {x'Oz}\)
Có \(\widehat {yOy'} = {\widehat O_2} + {\widehat O_3}\)\( = \frac{1}{2}\widehat {xOz} + \frac{1}{2}\widehat {x'Oz}\)\( = \frac{1}{2}\left( {\widehat {xOz} + \widehat {zOx'}} \right)\)
Mà \(\widehat {xOz}\) và \(\widehat {zOx'}\)là hai góc kề bù (giả thiết)
Nên \(\widehat {xOz} + \widehat {zOx'} = 180^\circ \) (tính chất hai góc kề bù)
Do đó \(\widehat {yOy'} = \frac{1}{2}{.180^o} = {90^o}\)
Suy ra Oy vuông góc với Oy'
Vậy định lí được chứng minh.
Vậy ta sắp xếp các bước như sau: (V) – (II) – (IV) – (III) – (I).
Ta chọn phương án B.
Câu 14:
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” và hình vẽ minh hoạ sau:
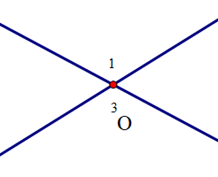
Viết giả thiết, kết luận cho định lí trên:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Giả thiết, kết luận cho định lí trên là:
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
Câu 15:
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” được minh hoạ bởi hình vẽ sau:
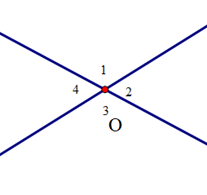
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra \({\widehat O_1} = {\widehat O_3}\) (vì cùng bù với \({\widehat O_2}\))”;
(II). “Ta có: \({\widehat O_1} + {\widehat O_2} = 180^\circ \)(hai góc kề bù) và \({\widehat O_2} + {\widehat O_3} = 180^\circ \)(hai góc kề bù)”;
(III). “Suy ra \({\widehat O_2} = {\widehat O_4}\) (vì cùng bù với \({\widehat O_3}\))
Vậy định lí được chứng minh.”;
(IV). “Lại có: \[{\widehat O_2} + {\widehat O_3} = 180^\circ \](hai góc kề bù) và \({\widehat O_3} + {\widehat O_4} = 180^\circ \)(hai góc kề bù)”.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Để chứng minh định lí trên, ta làm như sau:
Ta có: \({\widehat O_1} + {\widehat O_2} = 180^\circ \)(hai góc kề bù) và \({\widehat O_2} + {\widehat O_3} = 180^\circ \)(hai góc kề bù)
Suy ra \({\widehat O_1} = {\widehat O_3}\) (vì cùng bù với \({\widehat O_2}\))
Lại có: \[{\widehat O_2} + {\widehat O_3} = 180^\circ \](hai góc kề bù) và \({\widehat O_3} + {\widehat O_4} = 180^\circ \)(hai góc kề bù)
Suy ra \({\widehat O_2} = {\widehat O_4}\) (vì cùng bù với \({\widehat O_3}\))
Vậy định lí được chứng minh.
Vậy ta sắp xếp các câu trên theo thứ tự (II) – (I) – (IV) – (III).
Ta chọn phương án C.
Câu 16:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Hình A cho thấy đường thẳng a cắt hai đường thẳng song song b và c và hai góc ở vị trí so le trong bằng nhau.
Do đó hình A minh hoạ cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”.
Hình B kí hiệu góc tại đỉnh A và đỉnh B không phải là hai góc so le trong. Do đó B sai.
Hình C vẽ hai đường thẳng b và c không song song với nhau. Do đó C sai.
Hình D kí hiệu góc tại đỉnh A và đỉnh B không phải là hai góc so le trong. Do đó D sai.
Vậy ta chọn phương án A.
