Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) - Đề 4
-
1674 lượt thi
-
4 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Số lỗi chính tả trong một bài kiểm tra môn Anh văn của học sinh của lớp 7B được cô giáo ghi lại trong bảng dưới đây:
|
Giá trị (x) |
2 |
3 |
4 |
5 |
6 |
9 |
10 |
|
|
Tần số (n) |
3 |
6 |
9 |
5 |
7 |
1 |
1 |
N = 32 |
a) Dấu hiệu là gì? Tìm mốt của dấu hiệu.
b) Rút ra ba nhận xét về dấu hiệu.
c) Tìm số lỗi trung bình trong mỗi bài kiểm tra.
d) Dựng biểu đồ đoạn thẳng.
 Xem đáp án
Xem đáp án
a) Dấu hiệu là: Số lỗi chính tả trong một bài kiểm tra môn Anh văn mỗi học sinh lớp 7B.
Giá trị có tần số lớn nhất là 4 (tần số của giá trị 4 là 9).
Do đó, mốt của dấu hiệu là: Mo = 4 (lỗi).
b) Một số nhận xét:
- Có một bài kiểm tra mắc lỗi nhiều nhất là 10 lỗi, chiếm tỉ lệ 3,1%.
- Có ba bài kiểm tra mắc lỗi ít nhất là 2 lỗi chiếm tỉ lệ 9,3%.
- Phần nhiều bài kiểm tra mắc 4 lỗi chiếm tỉ lệ 27,9%.
c) Số trung bình cộng:
\(\overline X = \frac{{2\,.\,3 + 3\,.\,6\, + \,4\,.\,9 + 5\,.\,5 + 6\,.\,7 + 9\,.\,\,1 + 10\,.\,1}}{{32}} = \frac{{146}}{{32}} \approx 4,6\) (lỗi)
Vậy số lỗi trung bình trong mỗi bài kiểm tra là khoảng 4 lỗi.
d) Biểu đồ đoạn thẳng:
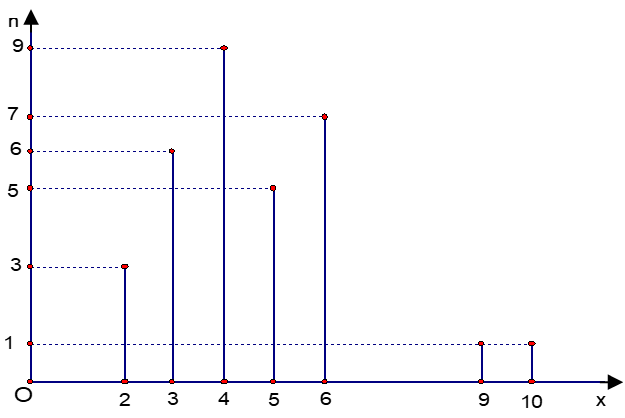
Câu 2:
Tính giá trị của biểu thức:
a) x2 – 3x + 1 tại x = 2.
b) \(2x - 5y + \frac{1}{3}\) tại x = 2 và y = −1.
 Xem đáp án
Xem đáp án
a) Thay x = 2 vào biểu thức x2 – 3x + 1, ta được:
22 – 3.2 + 1 = 4 – 6 + 1 = –1.
Vậy giá trị biểu thức x2 – 3x + 1 tại x = 2 là –1.
b) Thay x = 2 và y = −1 vào biểu thức \(2x - 5y + \frac{1}{3}\), ta được:
\(2x - 5y + \frac{1}{3} = 2\,.\,2 - 5\,( - 1) + \frac{1}{3} = \frac{{28}}{3}\).
Vậy giá trị của biểu thức \(2x - 5y + \frac{1}{3}\) tại x = 2 và y = −1 là \(\frac{{28}}{3}\).
Câu 3:
Cho ΔABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE ^ BC (E Î BC).
Chứng minh DA = DE.
c) ED cắt AB tại F. Chứng minh DADF = DEDC rồi suy ra DF > DE.
 Xem đáp án
Xem đáp án
|
GT |
ΔABC AB = 3 cm; AC = 4 cm; BC = 5 cm. BD là tia phân giác của \(\widehat {ABC}\) (\(D \in AC\)); DE ^ BC (E Î BC); \(ED \cap AB = F\). |
|
KL |
a) ΔABC vuông tại A. b) DA = DE. c) DADF = DEDC và DF > DE. |

a) Ta có: AB2 + AC2 = 32 + 42 = 9 + 16 = 25; BC2 = 52 = 25.
Vì AB2 + AC2 = BC2 nên áp dụng định lý Py-ta-go đảo ta suy ra ΔABC vuông tại A.
b) Vì ΔABC vuông tại A (câu a) nên \(\widehat {BAC} = {90^o}\).
Và DE ^ BC nên \(\widehat {BED} = {90^o}\).
Do đó \(\widehat {BAC} = \widehat {BED} = {90^o}\)
Xét ΔABD và ΔEBD có:
\(\widehat {BAC} = \widehat {BED} = {90^o}\) (cmt)
BD chung
\(\widehat {ABD} = \widehat {EBD}\) (vì BD là tia phân giác của \(\widehat {ABC}\))
Do đó ΔABD = ΔEBD (cạnh huyền – góc nhọn).
Suy ra DA = DE (hai cạnh tương ứng).
c) Xét DADF và DEDC có:
\(\widehat {DAF} = \widehat {DEC} = {90^o}\)
DA = DE (cmt)
\(\widehat {ADF} = \widehat {EDC}\) (đối đỉnh)
Do đó DADF = DEDC (c.g.c)
Suy ra DF = DC (hai cạnh tương ứng).
Mà DC > DE (cạnh đối diện với góc vuông có độ dài lớn nhất).
Do đó DF > DE.
Câu 4:
Tìm \(n \in \mathbb{Z}\) sao cho 2n − 3 ⋮ n + 1.
 Xem đáp án
Xem đáp án
Tìm \(n \in \mathbb{Z}\) sao cho 2n − 3 ⋮ n + 1.
Ta có 2n − 3 ⋮ n + 1
2(n + 1) − 5 ⋮ n + 1
Mà 2(n + 1) ⋮ n + 1
Nên 5 ⋮ n + 1.
Khi đó, n + 1 \( \in \) Ư(5) = {−1; 1; −5; 5}.
Ta có bảng sau:
|
n + 1 |
−1 |
1 |
−5 |
5 |
|
n |
−2 (TM) |
0 (TM) |
−6 (TM) |
4 (TM) |
Vậy để 2n − 3 ⋮ n + 1 thì n \( \in \) {−6; −2; 0; 4}.
