Trắc nghiệm Bài 7. Tập hợp số thực có đáp án
-
678 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
Số hữu tỉ là số viết dưới dạng phân số \(\frac{a}{b}\)với \(a,b \in \mathbb{Z},b \ne 0\). Gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
3,4 là số thập phân hữu hạn.
1,(231) là số thập phân vô hạn tuần hoàn.
6,74283… có phần tập phân không tuần hoàn nên 6,74283… là số thập phân vô hạn không tuần hoàn
\( - \sqrt {25} = - \sqrt {{5^2}} = - 5 = - 5,0\) số thập phân hữu hạn.
\(3\frac{5}{7} = 3 + \frac{5}{7} = \frac{{26}}{7} = 3,(713285)\)là số thập phân vô hạn tuần hoàn
Câu 2:
A =
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: B
Số vô tỉ là các số có dạng số thập phân vô hạn không tuần hoàn.
3,22143… có phần thập phân không tuần hoàn nên 3,22143… là số thập phân vô hạn không tuần hoàn.
1,4(21) là số thập phân vô hạn tuần hoàn.
\(3\frac{5}{7} = 3 + \frac{5}{7} = \frac{{26}}{7} = 3,(713285)\) là số thập phân vô hạn tuần hoàn.
\(\frac{4}{3}\) = 1,(3) là số thập phân vô hạn tuần hoàn.
\( - \sqrt 8 = - 2,828427...\) có phần thập phân không tuần hoàn nên -2,828427… là số thập phân vô hạn không tuần hoàn.
Câu 3:
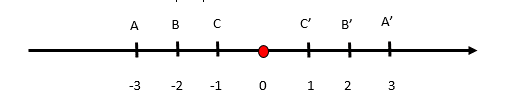
Viết tập hợp A’ có các phần tử là số đối của các phần tử của tập hợp A.
A = \(\left\{ {7;{\rm{ }}2,34521...;{\rm{ }}3\frac{1}{2};{\rm{ }} - \sqrt {25} } \right\}\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: D
Số đối là nghịch đảo phép cộng của một số a là số mà khi cộng với a cho kết quả 0. Số đối của a là –a.
Nên ta có số đối của:
Số đối của 7 là -7
Số đối của 2,34521… là -2.34521…
Số đối của \(3\frac{1}{2} = 3 + \frac{1}{2} = \frac{7}{2}\)là \( - \frac{7}{2}\)
Số đối của \( - \sqrt {25} = - \sqrt {{5^2}} = - 5\)là 5
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: D
\(\left| {{x^2}} \right| = 49\)
x2 = 49
x2 = 72 = (-7)2
x = 7 hoặc x = -7
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
\(\left| x \right| = \sqrt {25} \)
\(\left| x \right| = \sqrt {{5^2}} \)
\(\left| x \right| = 5\)
x = 5 hoặc x = -5
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: A
\(\left| {2x - 7} \right| = \sqrt {16} \)
\(\left| {2x - 7} \right| = \sqrt {{4^2}} \)
|2x – 7| = 4
\(2x - 7 = 4\)hoặc \(2x - 7 = - 4\)
Nếu 2x – 7 = 4 thì ta có:
2x – 7 = 4
2x = 4 + 7
2x = 11
x = \(\frac{{11}}{2}\)
Nếu 2x – 7 = -4 thì ta có:
2x - 7 = -4
2x = -4 + 7
2x = 3
x = \(\frac{3}{2}\)= 1,5
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
\(\left| {{x^2}} \right| \le 4\)
\(\left| {{x^2}} \right| \le {2^2}\)
\({x^2} \le {2^2}\)hoặc\({x^2} \le {( - 2)^2}\)
Nếu \(x \ge 0\)thì \(x \le 2\)thì x={0; 1; 2} (do x là số nguyên)
Nếu \(x < 0\)thì \(x \ge - 2\)thì x={-1; -2} (do x là số nguyên)
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
Ta có: \(\left| {\sqrt 4 } \right| = \left| {\sqrt {{2^2}} } \right| = \left| 2 \right| = 2\)
Câu 9:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
Ta có: \(\left| {\sqrt 9 } \right| = \left| {\sqrt {{3^2}} } \right| = \left| 3 \right| = 3\)
Số đối của 3 là -3.
Câu 10:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: B
\(\left| { - 2\frac{1}{4}} \right| = \left| { - \left( {2 + \frac{1}{4}} \right)} \right| = \left| { - \frac{9}{4}} \right| = \frac{9}{4}\)
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: A
\(\left| { - 3} \right| = 3\)
\(\left| {\frac{3}{2}} \right| = \frac{3}{2} = 1,5\)
Mà 3 > 1,5 nên \(\left| { - 3} \right|\) > \(\left| {\frac{3}{2}} \right|\)
Câu 12:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: D
\(\left| { - 1\frac{4}{5}} \right| = \left| { - \left( {1 + \frac{4}{5}} \right)} \right| = \left| { - \frac{9}{5}} \right| = \frac{9}{5}\)
\(\left| {\frac{9}{5}} \right| = \frac{9}{5}\)
Mà \(\frac{9}{5} = \frac{9}{5}\)nên \(\left| { - 1\frac{4}{5}} \right|\) = \(\left| {\frac{9}{5}} \right|\)
Câu 13:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: C
\(x = \frac{4}{3} = 1,(3)\)hoặc \(x = - \frac{4}{3} = - 1,(3)\)
Câu 14:

 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: D
Đoạn thẳng đơn vị được chia thành 5 phần bằng nhau. Đoạn thẳng OA chiếm 2 đơn vị mới (đơn vị mới bằng \(\frac{1}{5}\) đơn vị cũ). Mà A nằm bên trái O , do đó A biểu diện số âm.
Vậy điểm A biểu diễn số \(\frac{{ - 2}}{5}\).
Câu 15:
 Xem đáp án
Xem đáp án
Hướng dẫn giải\(\)
Đáp án đúng là: A
\(\sqrt {\left| { - 7} \right|} = \sqrt 7 \)
\(\sqrt 5 = \sqrt 5 \)
Mà 5 < 7 nên \(\sqrt 5 \) < \(\sqrt {\left| { - 7} \right|} \)
