15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Định lý Pytago có đáp án (Thông hiểu)

Câu 1:

Câu 1: Cho tam giác ABC vuông cân ở A. Tính độ dài BC, biết $A B = A C = 2 d m$ .

A. $B C = 4 d m$

B. $B C = \sqrt{6} d m$

C. $B C = 8 d m$

D. $B C = \sqrt{8} d m$

Xem đáp án

Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:

$A B^{2} + A C^{2} = B C^{2}$ mà $A B = A C = 2 d m$

Nên $B C^{2} = 2^{2} + 2^{2} = 8 \Rightarrow B C = \sqrt{8} (d m)$

Đáp án cần chọn là D

Câu 2:

Câu 2: Cho tam giác ABC vuông cân ở A. Tính độ dài BC, biết $A B = A C = 4 d m$ .

A. $B C = 6 d m$

B. $B C = \sqrt{23} d m$

C. $B C = 4 d m$

D. $B C = \sqrt{32} d m$

Xem đáp án

Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:

$A B^{2} + A C^{2} = B C^{2}$ mà $A B = A C = 4 d m$

Nên $B C^{2} = 4^{2} + 4^{2} = 32 \Rightarrow B C = \sqrt{32} (d m)$

Đáp án cần chọn là D

Câu 3:

Câu 3: Một tam giác có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.

A. 12 cm; 24 cm

B. 10 cm; 22 cm

C. 10 cm; 24 cm

D. 15 cm; 24 cm

Xem đáp án

Gọi độ dài hai cạnh góc vuông là x; y $(x; y > 0)$

Theo định lí Pytago ta có:

$x^{2} + y^{2} = 20^{2} \Leftrightarrow x^{2} + y^{2} = 400$

Theo bài ra ta có:

$\begin{array}{l} \frac{x}{3} = \frac{y}{4} \Rightarrow \frac{x^{2}}{9} = \frac{y^{2}}{16} = \frac{x^{2} + y^{2}}{9 + 16} = \frac{400}{25} = 16 \\ \Rightarrow x^{2} = 16.9 = 144 \Rightarrow x = 12 c m \\ y^{2} = 16.14 = 256 \Rightarrow y = 16 c m \end{array}$

Vậy các cạnh góc vuông có độ dài 10 cm; 24 cm

Đáp án cần chọn là C

Câu 4:

Câu 5: Cho tam giác ABC vuông ở A có $A C = 20 c m$ . Kẻ AH vuông góc BC. Biết $B H = 9 c m; H C = 16 c m$ . Tính AB, AH.

A. $A H = 12 c m; A B = 15 c m$

B. $A H = 10 c m; A B = 15 c m$

C. $A H = 15 c m; A B = 12 c m$

D. $A H = 12 c m; A B = 13 c m$

Xem đáp án

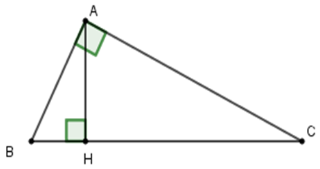
Ta có: $B C = B H + H C = 9 + 16 = 25 c m$

Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:

$\begin{array}{l} A B^{2} + A C^{2} = B C^{2} \Rightarrow A B^{2} + 20^{2} = 25^{2} \Leftrightarrow A B^{2} = 625 - 400 = 225 \\ \Rightarrow A B = 15 c m \end{array}$

Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

$\begin{array}{l} H A^{2} + H B^{2} = A B^{2} \Rightarrow H A^{2} + 9^{2} = 225 \Rightarrow H A^{2} = 225 - 81 = 144 \\ \Rightarrow H A = 12 c m \end{array}$

Vậy $A H = 12 c m; A B = 15 c m$

Đáp án cần chọn là A

Câu 5:

Câu 6: Cho tam giác ABC vuông ở A có $A C = 8 c m$ . Kẻ AH vuông góc BC. Biết $B H = 3, 6 c m; H C = 6, 4 c m$ . Tính AB, AH.

A. $A H = 4, 8 c m; A B = 6 c m$

B. $A H = 8, 4 c m; A B = 6 c m$

C. $A H = 4 c m; A B = 6 c m$

D. $A H = 5 c m; A B = 6 c m$

Xem đáp án

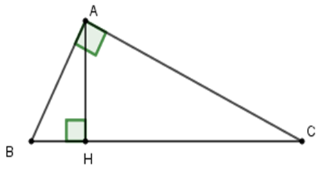
Ta có: $B C = B H + H C = 3, 6 + 6, 4 = 10 c m$

Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:

$\begin{array}{l} A B^{2} + A C^{2} = B C^{2} \Rightarrow A B^{2} + 8^{2} = 10^{2} \Leftrightarrow A B^{2} = 100 - 64 = 36 \\ \Rightarrow A B = \sqrt{36} = 6 c m \end{array}$

Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

$\begin{array}{l} H A^{2} + H B^{2} = A B^{2} \Rightarrow H A^{2} + 3, 6^{2} = 6^{2} \Rightarrow H A^{2} = 6^{2} - 3, 6^{2} = 23, 04 \\ \Rightarrow H A = \sqrt{23, 04} = 4, 8 c m \end{array}$

Vậy $A H = 4, 8 c m; A B = 6 c m$

Đáp án cần chọn là A

Câu 6:

Câu 7: Cho hình vẽ. Tính x.

A. $x = 10 c m$

B. $x = 11 c m$

C. $x = 8 c m$

D. $x = 5 c m$

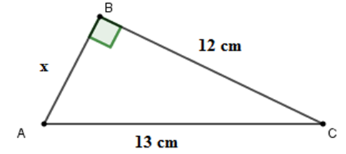
Xem đáp án

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:

$\begin{array}{l} A C^{2} = A B^{2} + B C^{2} \Rightarrow A B^{2} = A C^{2} - B C^{2} \\ \Rightarrow x^{2} = 13^{2} - 12^{2} = 25 \Rightarrow x = 5 c m \end{array}$

Vậy $x = 5 c m$

Đáp án cần chọn là D

Câu 7:

Câu 8: Cho hình vẽ. Tính x.

A. $x = 22 c m$

B. $x = 32 c m$

C. $x = 20 c m$

D. $x = 24 c m$

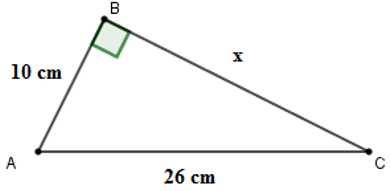
Xem đáp án

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:

$\begin{array}{l} A C^{2} = A B^{2} + B C^{2} \Rightarrow B C^{2} = A C^{2} - A B^{2} \\ \Rightarrow x^{2} = 26^{2} - 10^{2} = 576 \Rightarrow x = 24 c m \end{array}$

Vậy $x = 24 c m$

Đáp án cần chọn là D

Câu 8:

Câu 9.1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho $A H = 4 c m, A B = 5 c m$ . Tính BH.

A. 2cm

B. 5cm

C. 3cm

D. 4cm

Xem đáp án

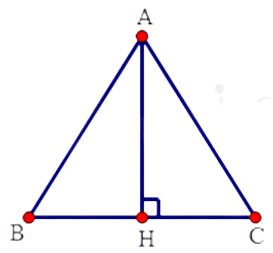
Áp dụng định lý Pytago vào tam giác ABH vuông tại H ta có:

$\begin{array}{l} A B^{2} = B H^{2} + A H^{2} \Rightarrow B H^{2} = A B^{2} - A H^{2} \\ \Rightarrow B H^{2} = 5^{2} - 4^{2} = 9 \Rightarrow B H = \sqrt{9} = 3 (c m) \end{array}$

Đáp án cần chọn là C

Câu 9:

Câu 9.2: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho $A H = 4 c m, A B = 5 c m$ . Tính chu vi tam giác ABC.

A. 18cm

B. 15cm

C. 16cm

D. 20cm

Xem đáp án

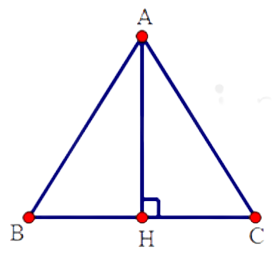
Áp dụng kết quả câu trước có $B H = 3 c m$

$Δ A B C$ cân tại A nên $A B = A C = 5 c m$

Áp dụng định lí Pytago vào tam giác ACH vuông tại H ta có:

$\begin{array}{l} A C^{2} = C H^{2} + A H^{2} \Rightarrow C H^{2} = A C^{2} - A H^{2} \\ \Rightarrow C H^{2} = 5^{2} - 4^{2} = 9 \Rightarrow C H = \sqrt{9} = 3 (c m) \end{array}$

Suy ra $B C = B H + C H = 3 + 3 = 6$ (cm)

Vậy chu vi tam giác ABC là:

$A B + A C + B C = 5 + 5 + 6 = 16 (c m)$

Đáp án cần chọn là C

Câu 10:

Câu 10: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:

A. 15cm; 8cm; 18cm

B. 21dm; 20dm; 29dm

C. 5m; 6m; 8m

D. 2m; 3m; 4m

Xem đáp án

+ Với bộ số 15cm; 8cm; 18cm ta thấy $18^{2} = 324; 15^{2} + 8^{2} = 289$

Nên $289 < 324 h a y 15^{2} + 8^{2} < 18^{2}$

Nên loại A

+ Với bộ số 21dm; 20dm; 29dm ta thấy $29^{2} = 841; 21^{2} + 20^{2} = 841$

Nên hay tam giác với độ dài 21dm; 20dm; 29dm thì tam giác đó là tam giác vuông (theo định lí Pytago đảo)

+Với bộ số 5m; 6m; 8m ta thấy $8^{2} = 64; 5^{2} + 6^{2} = 41 \Rightarrow 8^{2} > 5^{2} + 6^{2}$

Nên loại C

+ Với bộ số 2m; 3m; 4m ta thấy $4^{2} = 16; 2^{2} + 3^{2} = 13 \Rightarrow 4^{2} > 2^{2} + 3^{2}$

Nên loại D

Đáp án cần chọn là B

Câu 11:

Câu 11: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:

A. 11cm; 7cm; 8cm

B. 12dm; 15dm; 18dm

C. 9m; 12m; 15m

D. 6m; 7m; 9m

Xem đáp án

+ Với bộ số 11cm; 7cm; 8cm ta thấy $11^{2} = 121; 7^{2} + 8^{2} = 113 \Rightarrow 11^{2} > 7^{2} + 8^{2}$

Nên loại A

+ Với bộ số 12dm; 15dm; 18dm ta thấy $18^{2} = 324; 12^{2} + 15^{2} = 369 \Rightarrow 12^{2} + 15^{2} > 18^{2}$

Nên loại B

+ Với bộ số 9m; 12m; 15m ta thấy $15^{2} = 225; 9^{2} + 12^{2} = 225 \Rightarrow 9^{2} + 12^{2} = 15^{2}$

Theo định lí Pytago đảo, tam giác với ba cạnh có độ dài 9m; 12m; 15m là tam giác vuông

+Vói bộ số 6m; 7m; 9m ta thấy $9^{2} = 81; 6^{2} + 7^{2} = 85 \Rightarrow 6^{2} + 7^{2} > 9^{2}$

Nên loại D

Đáp án cần chọn là C

Câu 12:

Câu 12: Cho ABCD là hình vuông cạnh 4cm (hình vẽ). Khi đó, độ dài đường chéo AC là:

A. $A C = \sqrt{32} c m$

B. $A C = 5 c m$

C. $A C = \sqrt{30} c m$

D. $A C = 8 c m$

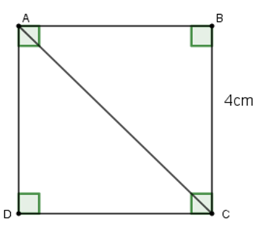
Xem đáp án

Vì ABCD là hình vuông nên $A B = B C = 4 c m$

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:

$A C^{2} = A B^{2} + B C^{2} = 4^{2} + 4^{2} = 32 \Rightarrow A C = \sqrt{32} (c m)$

Đáp án cần chọn là A

Câu 13:

Câu 13: Cho ABCD là hình vuông cạnh x cm (hình vẽ). Biết độ dài đường chéo AC là 6cm. Bình phương độ dài cạnh của hình vuông là:

A. 20cm

B. 18cm

C. 6cm

D. 16cm

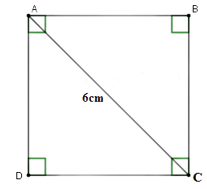
Xem đáp án

Vì ABCD là hình vuông nên $A B = B C = a (c m)$

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:

$\begin{array}{l} A C^{2} = A B^{2} + B C^{2} \\ \Rightarrow 6^{2} = a^{2} + a^{2} \\ \Rightarrow 2 a^{2} = 36 \\ \Rightarrow a^{2} = 36 : 2 = 18 \end{array}$

Vậy bình phương độ dài cạnh của hình vuông là 18

Đáp án cần chọn là B

Câu 14:

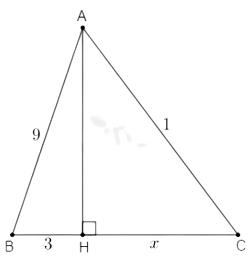
Câu 14: Tính x trong hình vẽ sau:

A. $x = 6$

B. $x = 7$

C. $x = 8$

D. $x = 5$

Xem đáp án

Áp dụng định lí Pytago vào vuông tại H ta có:

$\begin{array}{l} A B^{2} = A H^{2} + B H^{2} \\ \Rightarrow A H^{2} = A B^{2} - B H^{2} = 9^{2} - 3^{2} = 72 \end{array}$

Áp dụng định lí Pytago vào vuông tại H ta có:

$\begin{array}{l} A C^{2} = A H^{2} + C H^{2} \\ \Rightarrow H C^{2} = A C^{2} - A H^{2} = 11^{2} - 72 = 49 \\ \Rightarrow x = H C = \sqrt{49} = 7 \end{array}$

Đáp án cần chọn là B

Câu 15:

Câu 15: Một tam giác có độ dào ba cạnh là 10 cm; 6 cm; 8 cm. Tam giác đó là tam giác gì?

A. Tam giác cân

B. Tam giác vuông

C. Tam giác vuông cân

D. Tam giác đều

Xem đáp án

Ta có: $10^{2} = 100$

$8^{2} + 6^{2} = 64 + 36 = 100 \Rightarrow 8^{2} + 6^{2} = 10^{2}$

Theo định lý Py – ta – go đảo suy ra tam giác vuông.

Đáp án cần chọn là B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Định lý Pytago có đáp án

Trắc nghiệm Định lý Pytago có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương