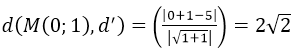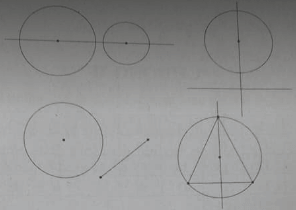25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Trắc nghiệm Đề kiểm tra Chương 1 Hình học 11 (có đáp án) (phần 1)

Trắc nghiệm tổng hơp Toán 11 (có đáp án)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41
Đề số 42
Đề số 43
Đề số 44
Đề số 45
Đề số 46
Đề số 47
Đề số 48
Đề số 49
Đề số 50
Đề số 51
Đề số 52
Đề số 53
Đề số 54
Đề số 55
Đề số 56
Đề số 57
Đề số 58
Đề số 59
Đề số 60
Đề số 61
Đề số 62
Đề số 63
Đề số 64
Đề số 65
Đề số 66
Đề số 67
Đề số 68
Đề số 69
Đề số 70
Đề số 71
Đề số 72
Đề số 73
Đề số 74
Đề số 75

Trắc nghiệm Trắc nghiệm Đề kiểm tra Chương 1 Hình học 11 (có đáp án) (phần 1)

23475 lượt thi
25 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Trong mặt phẳng Oxy cho điểm A(2;5). Phép tịnh tiến theo vecto $\vec{u} (1; 2)$ biến A thành điểm nào trong các điểm sau?

A. B(3;1)

B. C(1;6)

C. D(3;7)

D. E(4;7)

Xem đáp án

Đáp án C

Câu 2:

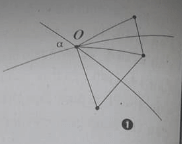
Cho đường thẳng a cắt hai đường thẳng song song b và b’. Có bao nhiêu phép tịnh tiến biến đường thẳng a bằng chính nó và biến đường thẳng b thành đường thẳng b’?

A. Không có phép tịnh tiến nào

B. Có một phép tịnh tiến duy nhất

C. Chỉ có hai phép tịnh tiến

D. Có vô số phép tịnh tiến

Xem đáp án

Giả sử a cắt b tại A, cắt b’ tại B (như hình vẽ).

Khi đó có duy nhất một vectơ tịnh tiến thỏa mãn yêu cầu bài toán là $\vec{A B}$ .

Ta có hình vẽ:

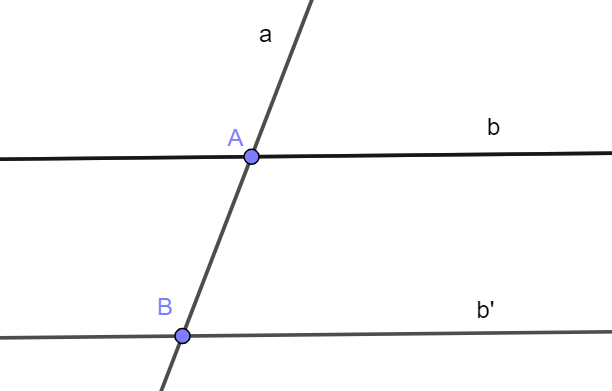
Đáp án B.

Câu 3:

Cho hai đường thẳng vuông góc với nhau a và b. có bao nhiêu phép đối xứng trục biến a thành a biến b thành b?

A. Không có phép đối xứng nào

B. có một phép đối xứng trục duy nhất

C. Chỉ có hai phép đối xứng trục

D. Có vô số phép đối xứng trục

Xem đáp án

$D_{a} v à D_{b}$

Đáp án C

Câu 4:

Cho hai đường tròn bằng nhau (O;R) và (O’;R) với tâm O và O’ phân biệt. có bao nhiêu phép vị tư biến (O;R) thành (O’;R) ?

A. Không có phép vị tự nào

B. Có một phép vị tự duy nhất

C. Chỉ có hai phép vị tự

D. Có vô số phép vị tự

Xem đáp án

Qua phép vị tự tỉ số k biến đường tròn (O; R) thành (O’; R).

Ta có: R’ = R nên |k| = 1

Suy ra: k = 1 hoặc k = -1

* Nếu k= 1 thì phép tự là phép đồng nhất: ( mâu thuẫn giả thiết)

* Khi k=-1 thì tâm vị tự là trung điểm của OO’.

Đáp án B

Câu 5:

Cho đường tròn (O;R). Có bao nhiêu phép vị tự tâm O biến (O;R) thành chính nó?

A. Không có phép vị tự nào

B. Có một phép vị tự duy nhất

C. Chỉ có hai phép vị tự

D. Có vô số phép vị tự

Xem đáp án

Phép vị tự tâm O tỉ số 1 và -1.

Đáp án C

Câu 6:

Cho đường tròn (O;R). Có bao nhiêu phép vị tự biến (O;R) thành chính nó?

A. Không có phép nào

B. Có một phép duy nhất

C. Chỉ có hai phép

D. Có vô số phép

Xem đáp án

Tâm vị tự bất kì, tỉ số vị tự k = 1.

Đáp án D

Câu 7:

Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

A. Không có phép nào

B. Có một phép duy nhất

C. Chỉ có hai phép

D. Có vô số phép

Xem đáp án

Có duy nhất một phép tịnh tiến biến đường tròn thành chính nó là phép tịnh tiến theo vecto $\vec{0}$

Chọn B

Câu 8:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình ${(x - 1)}^{2} + {(y + 2)}^{2} = 4$ . Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vecto $\vec{u} (2; 3)$ biến (C) thành đường tròn nào trong các đường tròn có phương trình là:

A. $x^{2} + y^{2} = 4$

B. ${(x - 2)}^{2} + {(y - 6)}^{2} = 4$

C. ${(x - 2)}^{2} + {(y - 3)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 1)}^{2} = 4$

Xem đáp án

+ Đường tròn (C) có tâm I(1; - 2) và bán kính R = 2.

+ Qua phép đối xứng trục Oy biến đường tròn (C) thàn đường tròn (C’); biến tâm I thành tâm I’(-1; -2) và R ‘ = R = 2

+ Qua phép tịnh tiến theo biến đường tròn (C’) thành đường tròn (C”), R”= R’ = R = 2

Biến tâm I’(-1; -2) thành tâm I” (x; y). Áp dụng công thức của phép tịnh tiến ta có:

$\{\begin{matrix} x = 2 + (- 1) = 1 \\ y = 3 + (- 2) = 1 \end{matrix} \Rightarrow I " (1; 1) $

Đường tròn (C”) có tâm I”(1; 1) và R” = 2 nên có phương trình:

${(x - 1)}^{2} + {(y - 1)}^{2} = 4$

Đáp án D

Câu 9:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x - 2y - 1 = 0. ảnh của đường thẳng d qua phép đối xứng tâm O có phương trình là:

A. 3x + 2y + 1 = 0

B. -3x + 2y -1 = 0

C. 3x + 2y - 1 = 0

D. 3x - 2y - 1 = 0

Xem đáp án

Qua phép đối xứng tâm O biến điểm M(x; y) thuộc đường thẳng d thẳng điểm M’ (x’; y’) thuộc đường thẳng d’.

Ta có: $\{\begin{matrix} x' = - x \\ y' = - y \end{matrix} \Leftrightarrow \{\begin{matrix} x = - x' \\ y = - y' \end{matrix}$

Vì điểm M thuộc d nên: 3x – 2y – 1 = 0

Suy ra: 3. (-x’) – 2(- y’) -1 = 0 hay - 3x’ + 2y’ – 1=0

Vây phương trình đường thẳng d’ là - 3x + 2y - 1= 0

Đáp án B

Câu 10:

Trong mặt phẳng Oxy cho điểm M(-3;2). ảnh của điểm M qua phép tịnh tiến theo $\vec{v} (2; 0)$ là:

A. (1;-1)

B. (-1;1)

C. (-1;2)

D. (1;-2)

Xem đáp án

$T_{\vec{v}} (M) = M' \Rightarrow \{\begin{matrix} x_{M'} = x_{M} + x_{\vec{v}} = - 3 + 2 = - 1 \\ y_{M'} = y_{M} + y_{\vec{v}} = 2 + 0 = 2 \end{matrix}$

Đáp án C

Câu 11:

Hợp thành của hai phép đối xứng qua hai đường thẳng cắt nhau là phép biến hình nào trong các phép biến hình dưới đây?

A. Phép đối xứng trục

B. Phép đối xứng tâm

C.Phép tịnh tiến

D. Phép quay

Xem đáp án

Phép quay tâm O góc quay 2α

Đáp án C

Câu 12:

Trong mặt phẳng tọa độ, cho đồ thị của hàm số y = sin⁡x. Có bao nhiêu phép tịnh tiến biến đồi thị đó thành chính nó?

A. Không

B. Một

C. Hai

D. Vô số

Xem đáp án

Ta biết rằng : $\sin x = \sin (x + k 2 π); k \in Z$

Do đó, nếu ta tịnh tiến đồ thị theo vecto $\vec{u} = k 2 π; k \in Z$ thì sẽ biến đồ thị đã cho thành chính nó .

Vì có vô số số nguyên k nên cũng có vô số phép tịnh tiến thỏa mãn đầu bài.

Đáp án D

Câu 13:

Cho hai đường thẳng d: x + y - 1 = 0 và d’: x + y - 5 = 0. Phép tịnh tiến theo vecto $\vec{u}$ biến đường thẳng d thành d’. khi đó, độ dài bé nhất của vecto $\vec{u}$ là bao nhiêu?

A. 5

B. 4√2

C. 2√2

D. √2

Xem đáp án

Độ dài bé nhất của vecto $\vec{u}$ bằng khoảng cách từ một điểm bất kì trên d tới d’ bằng:

Đáp án C

Câu 14:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + 3y - 3 = 0. Ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 biến đường thẳng d thành đường thẳng có phương trình là:

A. 2x + 3y - 6 = 0

B. 4x + 6y - 5 = 0

C. -2x - 3y + 3 = 0

D. 4x + 6y - 3 = 0

Xem đáp án

Đáp án A

Câu 15:

Trong mặt phẳng Oxy cho điểm M(2;4). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 1/2 và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào sau đây?

A. (-2;4)

B. (-1;2)

C. (1;2)

D. (1;-2)

Xem đáp án

Đáp án B

Câu 16:

Trong mặt phẳng Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc $45^{o}$ ?

A. (√2;0)

B. (-1;1)

C. (0;√2)

D. (1;0)

Xem đáp án

Đáp án A

Câu 17:

Có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Có 1 phép tịnh tiến duy nhất theo vectơ không biến hình vuông thành chính nó.

Đáp án B

Câu 18:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Có một phép tịnh tiến theo vecto khác vecto không biến mọi điểm thành điểm chính nó.

B. Có một phép đối xứng trục biến mọi điểm thành chính nó

C. Có một phép đối xứng tâm biến mọi điểm thành chính nó

D. Có một phép quay biến mọi điểm thành chính nó

Xem đáp án

Phép quay tâm I bất kì, góc quay k2π.

Đáp án D

Câu 19:

Trong các mệnh đề sau, mệnh đề nào sai?

A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng

B. Hình gồm một đường tròn và một đoạn thẳng tùy ý không có trục xứng.

C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng

D. Hình gồm một tam giác cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng

Xem đáp án

Hình gồm một đường tròn và một đoạn thẳng không có trục đối xứng.

Đáp án B

Câu 20:

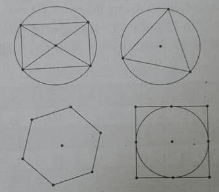
Trong các hình sau đây, hình nào không có tâm đối xứng?

A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp

B. Hình gồm một đường tròn và một tam giác đều nội tiếp

C. Hình lục giác đều

D. Hình gồm một hình vuông và đường tròn nội tiếp

Xem đáp án

Hình gồm một đường tròn và một tam giác đều nội tiếp không có tâm đối xứng.

Đáp án B

Câu 21:

Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?

A. không có

B. một

C. hai

D. vô số

Xem đáp án

Vecto tịnh tiến cùng phương với d.

Đáp án D

Câu 22:

Trong mặt phẳng Oxy cho đường thẳng d: x = 2. Trong các đường thẳng sau, đường nào là ảnh của d qua phép đối xứng tâm O?

A. x = 2

B. y = 2

C. y = -2

D. x = y

Xem đáp án

Vẽ hình trên mặt phẳng tọa độ Oxy.

Đáp án A

Câu 23:

Trong mặt phẳng Oxy cho đường thẳng d: 2x - y + 1 = 0. Để phép tịnh tiến theo vecto $\vec{u}$ biến d thành chính nó thì $\vec{u}$ phải là vecto nào trong các vecto sau?

A. $\vec{u} (2; 1)$

B. $u \to (2; - 1)$

C. $\vec{u} (2; 1)$

D. $\vec{u} (0; 1)$

Xem đáp án

Vecto tịnh tiến cùng phương với d.

Đáp án C

Câu 24:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: ${(x - 1)}^{2} + {(y - 2)}^{2} = 4$ . Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?

A. ${(x - 2)}^{2} + {(y - 4)}^{2} = 4$

B. ${(x + 2)}^{2} + {(y + 4)}^{2} = 4$

C. ${(x - 2)}^{2} + {(y - 4)}^{2} = 16$

D. ${(x + 2)}^{2} + {(y + 4)}^{2} = 16$

Xem đáp án

Đáp án D

Câu 25:

Cho P, Q cố định. Phép biến hình F biến điểm M bất kì thành M' sao cho $\vec{M M'} = 2 \vec{P Q}$ . Lúc đó F là:

A. Phép tịnh tiến theo vecto $\vec{P Q}$

B. Phép tịnh tiến theo vecto $\vec{M M'}$

C. Phép tịnh tiến theo vecto 2 $\vec{P Q}$

D. Phép tịnh tiến theo vecto $\vec{M P} + \vec{M Q}$

Xem đáp án

Đáp án C

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm tổng hơp Toán 11 (có đáp án)

Trắc nghiệm Trắc nghiệm Đề kiểm tra Chương 1 Hình học 11 (có đáp án) (phần 1)

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương