- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
Trắc nghiệm Tổ hợp xác suất từ đề thi đại học (có lời giải chi tiết) (phần 5)
-
28230 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm hệ số của số hạng chứa trong khai triển nhị thức Niutơn
 Xem đáp án
Xem đáp án
Chọn D
Xét khai triển nhị thức Niutơn: 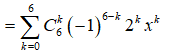
Số hạng chứa trong khai triển ứng với k = 3.
Vậy hệ số của số hạng chứa trong khai triển là: ![]() .
.
Câu 2:
Hệ số của số hạng chứa trong khai triển là
 Xem đáp án
Xem đáp án
Chọn B.
có công thức số hạng tổng quát là: ![]() .
.
Với k = 4, ta được số hạng ![]() .
.
Vậy hệ số của số hạng chứa trong khai triển là 810.
Câu 3:
Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
 Xem đáp án
Xem đáp án
Chọn C
Khai triển có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013
Câu 4:
Cho biểu thức: P(x) = . Hệ số của số hạng chứa trong khai triển thành đa thức của P(x) là
 Xem đáp án
Xem đáp án
Chọn C
Ta có: 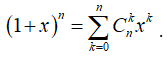 .
.
Số hạng tổng quát của khai triển là: ![]() . Hệ số của trong khai triển là:
. Hệ số của trong khai triển là:
Hệ số của số hạng chứa trong biểu thức P(x) là:
![]() .
.
Câu 5:
Số hạng không chứa z trong khai triển là?
 Xem đáp án
Xem đáp án
Chọn D
Có: 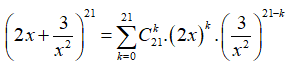
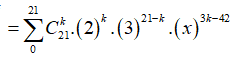
+ Số hạng không chứa x khi ![]()
![]()
+ Vậy số hạng không chứa x là ![]() .
.
Câu 6:
Tìm số hạng không chứa x trong khai triển nhị thức Newton
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát của biểu thức khi khai triển theo công thức nhị thức Newton là 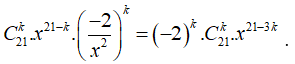
Số hạng không chứa x trong khai triển nhị thức Newton là ![]() với k thỏa mãn
với k thỏa mãn
21-3k = 0 => k = 7
Vậy số hạng không chứa x trong khai triển nhị thức Newton là ![]()
Câu 7:
Cho khai triển với n là số nguyên dương. Tìm hệ số của số hạng chứa trong khai triển biết .
 Xem đáp án
Xem đáp án
Chọn D
Ta có: ![]()
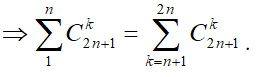
Ta có: 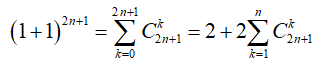
![]()
Hệ số của số hạng chứa là: = 120.
Câu 8:
Hệ số của trong khai triển biểu thức bằng.
 Xem đáp án
Xem đáp án
Chọn D
Hệ số của trong khai triển biểu thức là hệ số của trong khai triển biểu thức và bằng ![]() .
.
Hệ số của trong khai triển biểu thức là hệ số của trong khai triển biểu thức và bằng ![]() .
.
Vậy hệ số của trong khai triển biểu thức bằng 3240 + 80 = 3320.
Câu 9:
Tìm hệ số của số hạng không chứa x trong khai triển
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát trong khai triển là 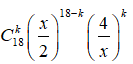
![]() .
.![]()
Số hạng không chứa x nên 18-2k = 0 => k = 9.
Hệ số của số hạng không chứa x trong khai triển là .
Câu 10:
Trong khai triển , số hạng không chứa x là
 Xem đáp án
Xem đáp án
Chọn B
Với x0, ta có
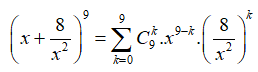
![]()
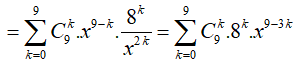
Từ yêu cầu bài toán suy ra 9 - 3k = 0 => k = 3, suy ra số hạng không chứa x là ![]() .
.
Câu 11:
Tìm hệ số của số hạng chứa trong khai triển
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển biểu thức ![]() là
là ![]()
![]()
Số hạng chứa ứng với k = 5, suy ra hệ số của số hạng chứa là:
![]()
Câu 12:
Số hạng không chứa x trong khai triển là
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát trong khai triển , x0 là  ,
, ![]() . Số hạng không chứa x ứng với 12-4k = 0 => k = 3.
. Số hạng không chứa x ứng với 12-4k = 0 => k = 3.
Vậy số hạng không chứa x trong khai triển trên là -1760.
Câu 13:
Tìm hệ số của số hạng chứa trong khai triển .
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
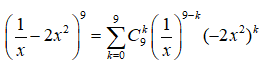
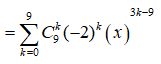
Hệ số cuả số hạng chứa tương ứng với 6 = 3k - 9 => k = 5
Vậy hệ số cuả số hạng chứa là
Câu 14:
Hệ số của trong khai triển biểu thức P(x) = x bằng
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa trong A(x) là![]()
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa trong B(x) là ![]()
Vậy hệ số của số hạng chứa trong khai triển P(x) đã cho là 240-13608 = -13368.
Câu 15:
Cho n là số nguyên dương thỏa mãn . Hệ số của số hạng chứa trong khai triển biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện xác định: ![]() .
.
Khi đó
![]()
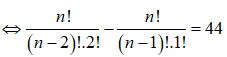
![]()

Kết hợp với điều kiện xác định suy ra n = 11
Ta có: 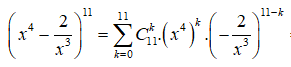
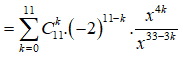
 .
.
Số hạng chứa ứng với k thỏa 7k - 33 = 9 => k = 6
Vậy hệ số của số hạng chứa là ![]() .
.
Câu 16:
Hệ số của trong khai triển của biểu thức là
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát trong khai triển của biểu thức là ![]() .
.
Do đó hệ số của (ứng với k = 2) là ![]() .
.
Câu 17:
Trong khai triển nhị thức , số hạng không chứa x là:
 Xem đáp án
Xem đáp án
Chọn C.
Số hạng tổng quát trong khai triển là:
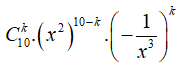
![]()
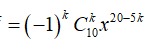
Số hạng không chứa x có số k thỏa mãn: 20 - 5k = 0 => k = 4
Vậy số hạng không chứa x đó là: ![]()
Câu 18:
Số hạng không chứa x trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn D
Ta có: 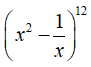

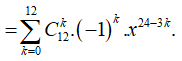
Vì số hạng không chứa x trong khai triển 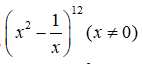 nên 24 - 3k = 0 => k = 8
nên 24 - 3k = 0 => k = 8
Vậy số hạng không chứa x trong khai triển là .
![]()
Câu 19:
Tìm số hạng không chứa x trong khai triển
 Xem đáp án
Xem đáp án
Chọn B
Ta có 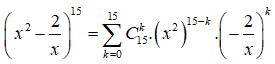
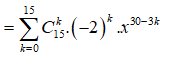
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là .
Câu 20:
Trong khai triển Newton của biểu thức , số hạng chứa là.
 Xem đáp án
Xem đáp án
Chọn B
Ta có: 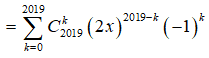
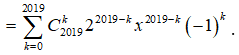
Số hạng tổng quát của khai triển là ![]() .
.
Để có thì 2019 - k = 18 => k = 2001.
Khi đó số hạng chứa là ![]() .
.
Câu 21:
Cho biểu thức P = với x > 0. Tìm số hạng không chứa x trong khai triển nhị thức Niutơn P.
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát trong khai triển 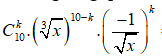
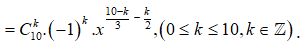 .
.
Số hạng không chứa x ứng với k thỏa mãn: 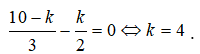 .
.
Vậy số hạng không chứa x cần tìm: ![]() .
.
Câu 22:
Biết tổng các hệ số trong khai triển nhị thức Newton của bằng . Tìm hệ số của .
 Xem đáp án
Xem đáp án
Chọn D
Ta có, 
 .
.
Tổng các hệ số trong khai triển bằng nên ta có phương trình:
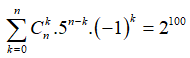
![]()
![]() .
.
Vậy 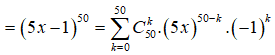
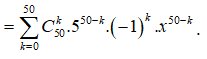 .
.
Xét số hạng chứa thì 50 - k = 3 => k = 47.
=> Hệ số của số hạng chứa là: ![]() .
.
Câu 23:
Tìm hệ số của số hạng chứa trong khai triển .
 Xem đáp án
Xem đáp án
Chọn B
Ta có có số hạng tổng quát là ![]() .
.
Số hạng chứa trong khai triển ứng với 8 - k = 5 => k = 3
Vậy hệ số của số hạng chứa trong khai triển là ![]() .
.
Câu 24:
Hệ số của trong khai triển của biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát của khai triển:
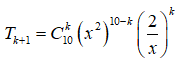
![]() .
.
Số hạng chứa ứng với: 20 - 3k = 2 => k = 6 (nhận).
Hệ số cần tìm là: ![]() .
.
Câu 25:
Tìm số hạng không chứa x trong khai triển , x0.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có 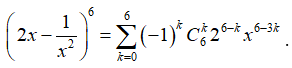 .
.
Số hạng thứ k + 1 là ![]() .
.
Tìm số hạng không chứa x trong khai triển khi: 6 - 3k = 0 => k = 2
Với k = 2 ta có số hạng không chứa x là: ![]() .
.
Câu 26:
Số hạng không chứa x trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Phân tích: Bài toán này ta phải nhớ được kiến thức lớp 11 về Nhị thức Niu – Tơn 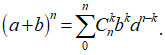 . Trong đó a, b thuộc số thực và n thuộc số tự nhiên và n 1. Số hạng tổng quát thứ k + 1 là:
. Trong đó a, b thuộc số thực và n thuộc số tự nhiên và n 1. Số hạng tổng quát thứ k + 1 là: ![]() .
.
Áp dụng vào bài toán ta có:
Số hạng tổng quát thứ k + 1 là: 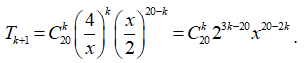 .
.
+) Vì số hạng không chứa x nên: 20 - 2k = 0 => k = 10
+) Vậy số hạng không chứa x là: ![]() .
.
Câu 27:
Cho đa thức f(x) = . Tìm hệ số , biết rằng: = 49152n
 Xem đáp án
Xem đáp án
Chọn D
Đạo hàm hai vế f(x)
![]()
![]()
![]()
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của ![]()
![]()
Câu 28:
Hệ số trong khai triển đa thức P(x) = có giá trị bằng đại lượng nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển là ![]()
![]() .
.
Số hạng này chứa khi 10 - k = 6 => k = 4.
Do đó hệ số trong khai triển là: ![]() .
.
Câu 30:
Số hạng không chứa x trong khai triển là
 Xem đáp án
Xem đáp án
Chọn D
Xét số hạng tổng quát
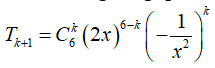

![]()
Số hạng không chứa x ứng với 6 - 3k = 0 => k = 2
Vậy số hạng không chứa x là ![]() .
.
Câu 31:
Tìm hệ số của số hạng chứa trong khai triển biết
 Xem đáp án
Xem đáp án
Chọn C
Ta có ![]()
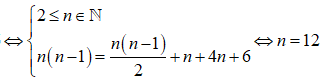 .
.
Xét khai triển 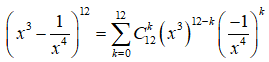
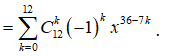 .
.
Số hạng chứa tương ứng với 36 - 7k = 8 => k = 4.
Vậy hệ số của số hạng chứa trong khai triển bằng ![]() .
.
Câu 32:
Cho số nguyên dương thỏa mãn = 0. Tìm hệ số của số hạng chứa trong khai triển nhị thức Niu-tơn của .
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện xác định:  .
.
Ta có: 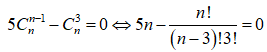
 .
.
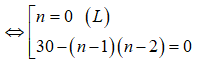 .
.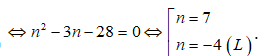
Khi đó nhị thức Niu-tơn 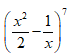 có số hạng tổng quát:
có số hạng tổng quát:

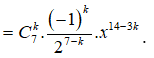 .
.
Số hạng chứa có giá trị k thỏa mãn: 14 - 3k = 5 => k = 3.
Vậy hệ số của số hạng chứa là: 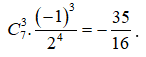 .
.
Câu 33:
Biết n là số nguyên dương thỏa mãn 3 số 0; theo thứ tự là số hạng đầu, số hạng thứ 3 và số hạng thứ 10 của một cấp số cộng. Hãy tìm số hạng không chứa x trong khai triển của
 Xem đáp án
Xem đáp án
Chọn A
Theo đề bài ta có: ![]()
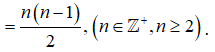 .
.
Lại theo tính chất của cấp số cộng có:
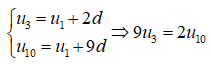
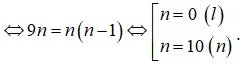
Khi đó số hạng tổng quát trong khai triển
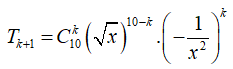
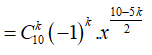
Số hạng không chứa x trong khai triển trên ứng với 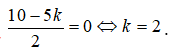
Vậy hệ số của số hạng không chứa x trong khai triển trên là ![]()
Câu 34:
Trong khai triển Newton của biểu thức , số hạng chứa là
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển là
![]()
![]()
![]()
Theo đề bài ta có: 2019 - k = 18 => k = 2001.
Vậy trong khai triển biểu thức đã cho, số hạng chứa là:
![]()
![]()
Câu 35:
Cho số nguyên dương n thỏa mãn điều kiện: 720. Hệ số của trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn B
Áp dụng công thức: ![]() ,
,![]() ta được:
ta được:
![]()
![]()
![]() .
.
Do đó : ![]()

![]()
Có: 
 .
.
Số hạng trong khai triển chứa ứng với 16 - 3k = 7 => k = 3
Vậy hệ số của là
Câu 36:
Cho khai triển . Hỏi có bao nhiêu giá trị của n 2019 sao cho tồn tại ![]() thỏa mãn .
thỏa mãn .
 Xem đáp án
Xem đáp án
Chọn D
Ta có: 
![]()
Số hạng tổng quát trong khai triển trên là ![]() nên từ giả thiết ta có
nên từ giả thiết ta có
![]()
Do đó: 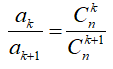
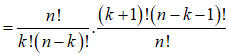
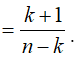
Suy ra: 
![]()
![]()
![]()
![]()
![]()
Thế vào (1), ta được: ![]()
![]()
Mặt khác, do ![]()
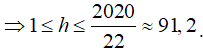
Với mỗi số nguyên dương h[1;91] tồn tại duy nhất một số nguyên dương n sao cho tồn tại k thỏa yêu cầu bài toán. Vậy có 91 số tự nhiên n.
Câu 37:
Cho n là số nguyên dương thỏa mãn = 78. Số hạng không chứa x trong khai triển bằng
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện: ![]()
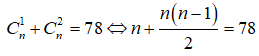
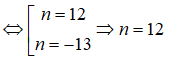 ( do điều kiện (1))
( do điều kiện (1))
Khi đó, 
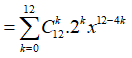
Số hạng không chứa x tương ứng 12 - 4k = 0 => k = 3
Suy ra số hạng không chứa x là: ![]()
Câu 38:
Cho khai triển , trong đó . Biết các hệ số thỏa mãn hệ thức . Hệ số bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta có: ![]()
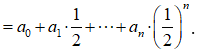
Trong khai triển thay x = ta được
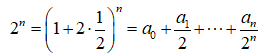
![]()
Số hạng tổng quát trong khai triển ![]()
Để có số hạng chứa thì k = 8.
Vậy ![]()
Câu 39:
Cho khai triển T =
 Xem đáp án
Xem đáp án
Chọn B
Cách 1:
![]()
![]()
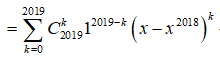
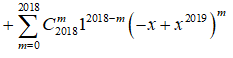

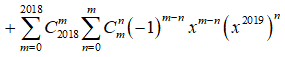
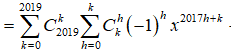

Với ![]()
![]()
Theo đề bài: 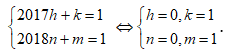
Hệ số của số hạng chứa x trong khai triển T là:
![]()
Cách 2:
Ta có: ![]() (với m = 4074342) (*)
(với m = 4074342) (*)
Lấy đạo hàm hai vế của (*) theo biến x:
![]()
![]()
Với x = 0, ta được: 2019 = .
Tương tự: ![]()
Lấy đạo hàm hai vế của (**) theo biến x:
![]()
![]()
Với x = 0, ta được: -2018 =
Hệ số của số hạng chứa x trong khai triển là: ![]()
Câu 40:
Tìm hệ số của số hạng chứa trong khai triển .
 Xem đáp án
Xem đáp án
Chọn A
![]()
![]()
![]()
Ta có các cặp (k;m): 2k + m = 5
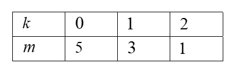
Suy ra hệ số của số hạng chứa là: ![]()
