10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2022 có đáp án (Đề 5)
-
6385 lượt thi
-
150 câu hỏi
-
195 phút
Danh sách câu hỏi
Câu 1:
Dựa vào dữ liệu đã cho, hãy cho biết ngành công nghiệp nào có tốc độ tăng trưởng nhanh nhất trong 8 tháng đầu năm 2019?

 Xem đáp án
Xem đáp án
Phương pháp giải:
Quan sát, đọc dữ liệu trên hình vẽ.
Giải chi tiết:
Dựa vào bảng số liệu đã cho ở trên ta thấy chỉ số sản xuất 8 tháng đầu năm 2019 là:
Khai khoáng: 102,5%
Chế biến, chế tạo: 110,6%
Sản xuất và phân phối điện: 110,2%
Cung cấp nước, hoạt động quản lý và xử lý rác thải, nước thải: 107,4% .
Như vậy: Chế biến chế tạo có tốc độ tăng trưởng cao nhất: 110,6%.
Chọn B.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Tính \({v_t}\, = \,{S_t}^\prime .\)
- Tìm GTLN của hàm số bậc hai.
Giải chi tiết:
\({S_t}\, = \,1\, + \,3{t^2}\, - \,{t^3}\, \Rightarrow \,{v_t}\, = \,{S_t}^\prime \, = \,6t\, - \,3{t^2}\)
Vận tốc của chuyển động đạt giá trị lớn nhất \( \Rightarrow \,{v_t}\,\max \, \Leftrightarrow \,\left( {6t\, - \,3{t^2}} \right)\,\max \)
Ta có: \({v_t}\, = \, - 3\left( {{t^2}\, - \,2t} \right)\, = \, - 3\left[ {\left( {{t^2}\, - \,2t\, + \,1} \right)\, - \,1} \right]\)
\(\begin{array}{l} = \,3\left[ {{{\left( {t\, - \,1} \right)}^2}\, - \,1} \right]\, = \, - 3{\left( {t - 1} \right)^2}\, + \,3\,\, \le \,\,3\\ \Rightarrow \,{v_t}\,\max \, = \,3\, \Leftrightarrow \,t\, = \,1\,\left( s \right)\end{array}\)
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp giải: Giải phương trình logarit cơ bản \({\log _a}f\left( x \right)\, = \,m\, \Leftrightarrow \,f\left( x \right)\, = \,{a^m}.\)
Giải chi tiết:
Điều kiện: \(3x\, - \,2\, > \,0\, \Leftrightarrow \,x\, > \,\frac{2}{3}\)
Ta có: \({\log _2}\left( {3x\, - \,2} \right)\, = \,3\, \Leftrightarrow \,3x\, - \,2\, = \,{2^3}\, \Leftrightarrow \,3x\, = \,10\, \Leftrightarrow \,x\, = \,\frac{{10}}{3}\,\left( {tm} \right)\)
Chọn B.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp giải: Giải phương trình logarit: \({\log _a}x\, = \,b\, \Leftrightarrow \,x\, = \,{a^b}.\)
Giải chi tiết:
\({\log _3}\,\left( {2x\, + \,1} \right)\, = \,2\, \Leftrightarrow \,2x\, + \,1\, = \,{3^2}\, \Leftrightarrow \,x\, = \,4\)
Chọn A.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Giải phương trình thứ nhất tìm \(y\)
- Thế \(y\)tìm được vào phương trình thứ hai. Tìm điều kiện để phương trình thứ hai vô nghiệm.
Giải chi tiết:
Xét phương trình:
\(\begin{array}{l}{y^2} - \left| y \right| = 6\\ \Leftrightarrow {\left| y \right|^2} - \left| y \right| - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| y \right|\, = \, - 2\,\left( {loai} \right)\\\left| y \right|\, = \,3\, \Leftrightarrow \,y\, = \, \pm \,3\,\end{array} \right.\end{array}\)
Với phương trình thứ hai trở thành \({x^2} - 2mx + 7 = 0\)(1)
Với phương trình thứ hai trở thành \({x^2} - 2mx + 1 = 0\)(2)
Để hệ phương trình đã cho có nghiệm thì phương trình (1) và (2) đều vô nghiệm:
Vậy có 1 giá trị nguyên của \(m\)thỏa mãn là \(m = 0\)
Chọn A.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp giải: Sử dụng phương trình mặt phẳng theo đoạn chắn :
Mặt phẳng \(\left( P \right)\) cắt \(Ox\,;\,Oy\,;\,Oz\) lần lượt tại \(A\left( {a\,;\,0\,;\,0} \right)\,,\,B\left( {0\,;\,b\,;\,0} \right)\,,\,C\left( {0\,;\,0;\,c} \right)\,\,\left( {a\,,\,b\,,\,c\, \ne \,0} \right)\) thì có phương trình \(\left( P \right)\,\,:\,\,\frac{x}{a}\, + \,\frac{y}{b}\, + \,\frac{z}{c}\, = \,1\)
Sử dụng công thức trọng tâm : \(M\) là trọng tâm \[\Delta \,ABC\] thì\(\left\{ \begin{array}{l}{x_M}\, = \,\frac{{{x_A}\, + \,{x_B}\, + \,{x_C}}}{3}\\{y_M}\, = \,\frac{{{y_A}\, + \,{y_B}\, + \,{y_C}}}{3}\\{z_M}\, = \,\frac{{{z_A}\, + \,{z_B}\, + \,{z_C}}}{3}\end{array} \right.\)
Giải chi tiết:
Theo đề bài ta có : \(A\left( {a\,;\,0\,;\,0} \right)\,,\,B\left( {0\,;\,b\,;\,0} \right)\,,\,C\left( {0\,;\,0;\,c} \right)\,\,\left( {a\,,\,b\,,\,c\, \ne \,0} \right)\)
Vì \(M\) là trọng tâm \[\Delta \,ABC\] nên \(\left\{ \begin{array}{l}{x_M}\, = \,\frac{{{x_A}\, + \,{x_B}\, + \,{x_C}}}{3}\\{y_M}\, = \,\frac{{{y_A}\, + \,{y_B}\, + \,{y_C}}}{3}\\{z_M}\, = \,\frac{{{z_A}\, + \,{z_B}\, + \,{z_C}}}{3}\end{array} \right.\, \Leftrightarrow \,\left\{ \begin{array}{l}1\, = \,\frac{a}{3}\\2\, = \,\frac{b}{3}\\3\, = \,\frac{c}{3}\end{array} \right.\, \Leftrightarrow \,\left\{ \begin{array}{l}a\, = \,3\\b\, = \,6\\c\, = \,9\end{array} \right.\)
Suy ra \(A\left( {3\,;\,0\,;\,0} \right)\,,\,B\left( {0\,;\,6\,;\,0} \right)\,,\,C\left( {0\,;\,0;\,9} \right)\)
Phương trình mặt phẳng \(\left( P \right)\) là \(\,\frac{x}{a}\, + \,\frac{y}{b}\, + \,\frac{z}{c}\, = \,1\, \Leftrightarrow \,6x\, + \,3y\, + \,2z\, - \,18\, = \,0\)
Chọn C.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp giải: Cho hai điểm \(A\left( {{x_1}\,;\,{x_2}\,;\,{x_3}} \right)\,,\,B\left( {{x_2}\,;\,{y_2}\,;\,{z_2}} \right)\) thì tọa độ trung điểm của \(AB\)là: \(I\left( {\frac{{{x_1}\, + \,{x_2}}}{2}\,;\,\frac{{{y_1}\, + \,{y_2}}}{2}\,;\,\frac{{{z_1}\, + \,{z_2}}}{2}} \right)\,.\)
Giải chi tiết:
Ta có: \(A\left( {1\,;\,2\,;\, - 3} \right)\,,\,B\left( {3\,;\, - 2\,;\,1} \right)\)
⇒ Tọa độ trung điểm \(I\) của \(AB\)là: \(I\left( {\frac{{1\, + \,3}}{2}\,;\,\frac{{2\, - \,2}}{2}\,;\,\frac{{ - 3\, + \,1}}{2}} \right)\,\, \Rightarrow \,I\left( {2\,;\,0\,;\, - 1} \right)\,.\)
Chọn B.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp giải: Lập bảng xét dấu, giải bất phương trình
Giải chi tiết:
\(\frac{{2x}}{{2{x^2} - 3x + 1}} \ge 0 \Leftrightarrow \frac{{2x + 1}}{{(2x - 1)(x + 1)}} \ge 0\) ĐKXĐ: \(\left\{ {\begin{array}{*{20}{c}}{x \ne 1}\\{x \ne \frac{1}{2}}\end{array}} \right.\)
Đặt \(f(x) = \frac{{2x}}{{2{x^2} - 3x + 1}}\). Ta có bảng:
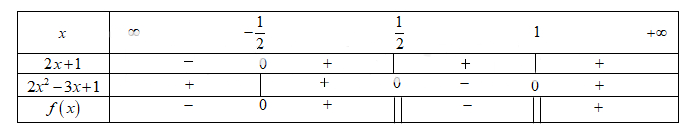
Vậy \(f\left( x \right)\, \ge \,0\, \Leftrightarrow \,x\, \in \,\left[ { - \frac{1}{2}\,;\,\frac{1}{2}} \right]\, \cup \,\left( {1\,;\, + \infty } \right)\)
Chọn B.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Giải chi tiết:
Phương pháp: Áp dụng công thức \(\sin x\, + \,\cos x\, = \,\sqrt 2 \sin \left( {x\, + \,\frac{\pi }{4}} \right)\)
Cách giải
\(\begin{array}{l}\sqrt 2 \sin \left( {x\, + \,\frac{\pi }{4}} \right)\, = \,\sqrt 2 \sin 5x\\ \Leftrightarrow \,\sin \left( {x\, + \,\frac{\pi }{4}} \right)\, = \,\sin 5x\\ \Leftrightarrow \,\left[ \begin{array}{l}x\, + \,\frac{\pi }{4}\, = \,5x\, + \,k2\pi \\x\, + \,\frac{\pi }{4}\, = \,\pi \, - \,5x\, + \,k2\pi \end{array} \right.\, \Leftrightarrow \,\left[ \begin{array}{l}x\, = \,\frac{\pi }{{16}}\, + \,k\frac{\pi }{2}\\x\, = \,\frac{\pi }{8}\, + \,k\frac{\pi }{3}\end{array} \right.\end{array}\)
Chọn đáp án C
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Diện tích bề mặt mỗi tầng (kể từ tầng 1) lập thành 1 cấp số nhân. Xác định công bội \(q\) và số hạng đầu \({u_1}\) của CSN đó.
- Sử dụng công thức SHTQ của CSN: \({u_n}\, = \,{u_1}\,{q^{n\, - \,1}}\).
Giải chi tiết:
Diện tích bề mặt mỗi tầng (kể từ tầng 1) lập thành 1 cấp số nhân có công bội \(q\, = \,\frac{1}{2}\) và \({u_n}\, = \,\frac{{12288}}{2}\, = \,6144\,\left( m \right)\).
Khi đó diện tích mặt trên cùng là: \({u_{11}}\, = \,{u_1}\,{q^{10}}\, = \,6144.{\left( {\frac{1}{2}} \right)^{10}}\, = \,6\,\,\left( {{m^2}} \right)\)
Chọn A.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp giải: \(\int {\frac{1}{{ax\, + \,b}}dx\, = \,\frac{1}{a}\ln \left| {ax\, + \,b} \right|\, + \,C} \)
Giải chi tiết:
\(\int {f\left( x \right)dx\, = \,\int {\frac{1}{{2x\, + \,3}}dx\, = \,\frac{1}{2}\int {\frac{{d\left( {2x\, + \,3} \right)}}{{2x\, + \,3}}\, = \,\frac{{\ln \left| {2x\, + \,3} \right|}}{2}\, + \,C} } } \)
Khi \(C\, = \,1\, \Rightarrow \) Đáp án A đúng.
Đáp án B: \(F\left( x \right)\, = \,\frac{{\ln {{\left| {2x\, + \,3} \right|}^2}}}{4}\, + \,3\, = \,\frac{{2\ln \left| {2x\, + \,3} \right|}}{4}\, + \,3\, = \,\frac{{\ln \left| {2x\, + \,3} \right|}}{2}\, + \,3\, \Rightarrow \,C\, = \,3\)
Đáp án D:
\(F\left( x \right)\, = \,\frac{{\ln \left| {x\, + \,\frac{3}{2}} \right|}}{2}\, + \,4\, = \,\frac{{\ln \left| {2x\, + \,3} \right|\, - \,\ln 2}}{2}\, + \,4\, = \,\frac{{\ln \left| {2x\, + \,3} \right|}}{2}\, - \,\frac{{\ln 2}}{2}\, + \,4\, \Rightarrow \,C\, = \, - \frac{{\ln 2}}{2}\, + \,4\)
\( \Rightarrow \,F\left( x \right)\, = \,\frac{{\ln \left| {4x\, + \,6} \right|}}{4}\, + \,2\) là khẳng định sai
Chọn C.
Câu 12:
Cho hàm số \(y\, = \,f\left( x \right)\). Hàm số \(y\, = \,f'\left( x \right)\) có đồ thị như sau:
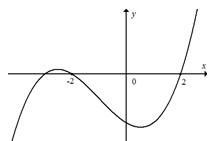
Bất phương trình \(f\left( x \right)\, > \,{x^2}\, - \,2x\, + \,m\) đúng với mọi \(x\, \in \,\left( {1\,;\,2} \right)\)khi và chỉ khi
 Xem đáp án
Xem đáp án
Phương pháp giải: Cô lập \(m\)
Giải chi tiết:
\(f(x) > {x^2} - 2x + m\forall x \in (1;2) \Leftrightarrow f(x) - {x^2} + 2x > m\forall x \in (1;2)\)
Đặt \[g(x) = f(x) - {x^2} + 2x \Rightarrow g(x) > m\,\,\forall x \in (1;2) \Leftrightarrow m \le \,\mathop {\min }\limits_{\left[ {1\,;\,2} \right]} g\left( x \right)\]
Ta có: \(g'(x) = f'(x) - 2x + 2 = 0 \Leftrightarrow f'(x) = 2x - 2\)
Vẽ đồ thị hàm số \(y = f'(x)\)và \(y = 2x - 2\)trên cùng một mặt phẳng tọa độ
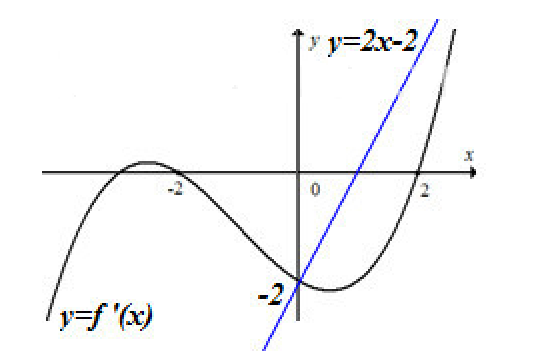
Dựa vào đồ thị hàm số ta thấy \(g'(x) = 0 \Leftrightarrow x = 0\)
BBT:
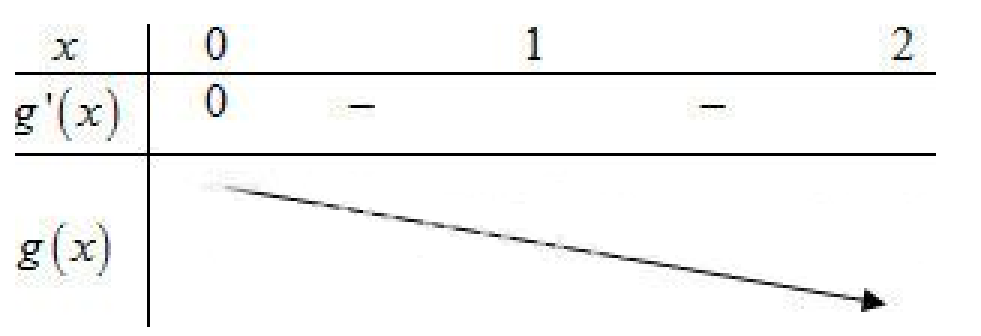
Từ BBT \[ \Rightarrow \,\mathop {\min }\limits_{\left[ {1\,;\,2} \right]} g\left( x \right)\, = \,g\left( x \right)\, = \,f\left( 2 \right)\, \Leftrightarrow \,m\, \le \,f\left( 2 \right)\]
Chọn A.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Sử dụng công thức tính quãng đường đi được của vật có vận tốc \(v\left( t \right)\) từ thời điểm đến \(t\, = \,a\) thời điểm \(t\, = \,b\) là: \(S\, = \,\int\limits_a^b {v\left( t \right)} \,dt\)
Giải chi tiết:
Thời điểm xe dừng hẳn thoả mãn \(v\left( t \right)\, = \,0\, \Leftrightarrow \,20\, - \,5t\, = \,0\, \Leftrightarrow \,t\, = \,4\)
Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh đến lúc mô tô dừng lại là
\(\int\limits_0^4 {\left( {20\, - \,5t} \right)\,dt} \, = \,40\)
Chọn D.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp giải: Sử dụng công thức lãi kép \({A_n}\, = \,A{\left( {1\, + \,r} \right)^n}\)
Giải chi tiết:
Giả sử sau n năm dân số nước ta đạt mức 120,5 triệu người ta có:
\(120,5\, = \,91,7\,{\left( {1\, + \,\frac{{1,1}}{{100}}} \right)^n}\, \Leftrightarrow \,n\, \approx \,24,97\)
Vậy phải sau 25 năm, tức là vào năm \(2015\, + \,25\, = \,2040\)
Chọn đáp án D.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp giải: Giải bất phương trình \({\log _a}f\left( x \right)\, < \,{\log _a}g\left( x \right)\, \Leftrightarrow \,\left[ \begin{array}{l}\left\{ \begin{array}{l}a\, > \,1\\f\left( x \right)\, < \,g\left( x \right)\end{array} \right.\\\left\{ \begin{array}{l}0\, < \,a\, < \,1\\f\left( x \right)\, > \,g\left( x \right)\end{array} \right.\end{array} \right.\)
Giải chi tiết:
Điều kiện: \(\left\{ \begin{array}{l}3x\, + \,1\, > \,0\\25\, - \,25x\, > \,0\end{array} \right.\, \Leftrightarrow \,\left\{ \begin{array}{l}x\, > \, - \frac{1}{3}\\x\, < \,1\end{array} \right.\, \Leftrightarrow \, - \frac{1}{3}\, < \,x\, < \,1.\)
\(\begin{array}{l}{\log _5}\left( {3x\, + \,1} \right)\, < \,{\log _5}\left( {25\, - \,25x} \right)\, \Leftrightarrow \,3x\, + \,1\, < \,25\, - \,25x\\ \Leftrightarrow \,28x\, < \,24\, \Leftrightarrow \,x\, < \,\frac{{24}}{{28}}\, \Leftrightarrow \,x\, < \,\frac{6}{7}\\ \Rightarrow \, - \frac{1}{3}\, < \,x\, < \,\frac{6}{7}\,.\end{array}\)
Chọn C.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc \(\left[ {0;2} \right]\)
- Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f(x)\), \(y = g(x)\), đường thẳng \(x = a,x = b\)khi quay quanh trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}(x) - {g^2}(x)} \right|} dx\)
Giải chi tiết:
ĐKXĐ: \(x \ne 4\)
Xét phương trình hoành độ giao điểm: \(\frac{4}{{x - 4}} = 0\)(vô nghiệm)
Thể tích khối tròn xoay cần tìm là: \(V = \pi \int\limits_0^2 {{{\left( {\frac{4}{{x - 4}}} \right)}^2}} dx = 4\pi \)
Chọn C.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp giải: Hàm số \(y\, = \,f\left( x \right)\) đồng biến trên \(\left( {a\,;\,b} \right)\) khi và chỉ khi \(f'\left( x \right)\, \ge \,0\,\forall x\, \in \,\left( {a\,;\,b} \right)\)và bằng 0 tại hữu hạn điểm.
Giải chi tiết:
TXĐ: \(D\, = \,\mathbb{R}\)
Ta có: \(y'\, = \,{x^2}\, - \,\left( {m\, + \,5} \right)x\, + \,5m.\)
Để hàm số đồng biến trên \(\left( {6\,;\,7} \right)\) thì \(y'\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\)
\(\begin{array}{l} \Rightarrow \,{x^2}\, - \,\left( {m\, + \,5} \right)x\, + \,5m\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\\ \Leftrightarrow \,{x^2}\, - \,mx\, - \,5x\, + \,5m\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\\ \Leftrightarrow \,x\left( {x\, - \,m} \right)\, - \,5\left( {x\, - \,m} \right)\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\\ \Leftrightarrow \,\left( {x\, - \,m} \right)\left( {x\, - \,5} \right)\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\end{array}\)
Do \(x\, \in \,\left( {6\,;\,7} \right)\) nên \(x\, - \,5\, > \,0\), khi đó ta có: \(x\, - \,m\, \ge \,0\,\forall x\, \in \,\left( {6\,;\,7} \right)\)
\( \Leftrightarrow \,m\, \le \,x\,\forall x\, \in \,\left( {6\,;\,7} \right)\, \Leftrightarrow \,m\, \le \,6\)
Vậy \(m\, \in \,\left( { - \infty \,;\,6} \right]\)
Đáp án B.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp giải: +) Tìm số phức \(z\)từ dữ kiện đề bài
+) Sử dụng \(z = a + bi \Rightarrow \bar z = a - bi\)
+) Mô đun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)
Giải chi tiết:
Gọi số phức \(z = a + bi\) \((a;b \in R)\)ta có:
\(\begin{array}{l}(1 + i)(z - i) + 2z + 2i\\ \Leftrightarrow (1 + i)z - (1 + i)i + 2z + 2i\\ \Leftrightarrow (3 + i)z + 3i - 1 \Leftrightarrow z = \frac{{3i - 1}}{{3 + i}} = i\end{array}\)
Từ đó \({\rm{w}} = \frac{{\bar z - 2z + 1}}{{{z^2}}} = \frac{{ - i\, - \,2i\, + \,1}}{{ - 1}} = \, - 1\, + \,3i\)
Suy ra
Chọn C.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Đặt \(z = x + yi\) \((x,y \in R)\)thay vào điều kiện bài cho tìm mối quan hệ của \(x,y\)và kết luận
Giải chi tiết:
Đặt \(z = x + yi\) \((x,y \in R)\)ta có:
\(\left| {z + 2 - i} \right| = 2 \Leftrightarrow \left| {x + yi + 2 - i} \right| = 2 \Leftrightarrow \left| {(x + 2) + (y - 1)i} \right| = 2\)
Vậy tập hợp điểm \(M\)biểu diễn số phức \(z\) là đường tròn \({\left( {x\, + \,2} \right)^2}\, + \,{\left( {y\, - \,1} \right)^2}\, = \,4\)
Chọn A.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp giải: Tìm giao điểm \[M\]của \[d,d'\]sau đó dựa vào \[d\left( {M;\Delta } \right)\]để tìm \[m\]
Giải chi tiết:
\[M = d \cap d' \Rightarrow M\left\{ {\begin{array}{*{20}{c}}{2x - y = 0}\\{x + 3y - 7 = 0}\end{array}} \right. \Rightarrow M\left( {1;2} \right)\]
\[d\left( {M;\Delta } \right) = \frac{{\left| {4.1 + 3.2 + m} \right|}}{{\sqrt {{4^2} + {3^2}} }} = \frac{{\left| {10 + m} \right|}}{5} = 2\]
Chọn C
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Xác định tọa độ tâm I thuộc đường thẳng \(\Delta \,:\,3x\, - \,y\, + \,10\, = \,0\)
\(\left( C \right)\) có tâm \(I\) qua hai điểm \(A\,,\,B\) nên \(IA\, = \,IB\)
Giải chi tiết:
Ta có:\(I\,\, \in \,\,\Delta \,:\,3x\, - \,y\, + \,10\, = \,0\, \Rightarrow \,I\left( {a\,;\,3a\, + \,10} \right)\)
Vì đường tròn \(\left( C \right)\)đi qua hai điểm \(A\left( { - 1\,;\,2} \right)\)và \(B\left( { - 2\,;\,3} \right)\) nên \(IA\, = \,IB\, = \,R\)
\[\begin{array}{l} \Rightarrow \,I{A^2}\, = \,I{B^2}\\ \Leftrightarrow \,{\left( {a\, + \,1} \right)^2}\, + \,{\left( {3a\, + \,8} \right)^2}\, = \,{\left( {a\, + \,2} \right)^2}\, + \,{\left( {3a\, + \,7} \right)^2}\\ \Leftrightarrow \,{a^2}\, + \,2a\, + \,1\, + \,9{a^2}\, + \,48a\, + \,64\, = \,{a^2}\, + \,4a\, + \,4\, + \,9{a^2}\, + \,42a\, + \,49\\ \Leftrightarrow \,50a\, + \,65\, = \,46a\, + \,53\\ \Leftrightarrow \,4a\, = \, - 12\\ \Leftrightarrow \,a\, = \, - 3\\ \Leftrightarrow \,\left\{ \begin{array}{l}a\, = \, - 3\\I\left( { - 3\,;\,1} \right)\\{R^2}\, = \,5\end{array} \right.\end{array}\]
Vậy đường tron \(\left( C \right)\)cần tìm là: \({\left( {x\, + \,3} \right)^2}\, + \,{\left( {y\, - \,1} \right)^2}\, = \,5\)
Chọn D.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp giải: - \[\left\{ {\begin{array}{*{20}{c}}{d \subset \left( Q \right)}\\{\left( P \right) \bot \left( Q \right)}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_d}} \, \bot \,\overrightarrow {{n_Q}} }\\{\overrightarrow {{n_P}} \, \bot \,\overrightarrow {{n_Q}} }\end{array}\,} \right.\, \Rightarrow \,\overrightarrow {{n_Q}} \, = \,\left[ {\overrightarrow {{u_d}} \,,\,\overrightarrow {{n_P}} \,} \right]\]
- Lấy \[M \in d\]bất kỳ suy ra \[M \in \left( Q \right)\]
- Viết phương trình mặt phẳng \[\left( Q \right)\]đi qua \[M\]và có 1 VTPT \[\overrightarrow {{n_Q}} \,\]vừa tìm được
- Biến đổi về đúng dạng \[\left( Q \right):ax + by + cz - 14 = 0\], đồng nhất hệ số tìm \[a,b,c\]
Giải chi tiết:
Đường thẳng \[d:\frac{x}{1} = \frac{{y - 2}}{1} = \frac{{z + 6}}{{ - 2}}\]có 1 VTCP là \[\overrightarrow {{u_d}} \,\, = \,(\,1\,;\,1\,;\, - 2)\]
Mặt phẳng \[\left( P \right):2x - 2y + z + 2021 = 0\]có 1 VTPT là \[\overrightarrow {{n_P}} \, = \,(2\,;\, - 2\,;\,1)\]
Vì \[\left\{ {\begin{array}{*{20}{c}}{d \subset \left( Q \right)}\\{\left( P \right) \bot \left( Q \right)}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_d}} \, \bot \,\overrightarrow {{n_Q}} }\\{\overrightarrow {{n_P}} \, \bot \,\overrightarrow {{n_Q}} }\end{array}\,} \right.\, \Rightarrow \,\overrightarrow {{n_Q}} \, = \,\left[ {\overrightarrow {{u_d}} \,,\,\overrightarrow {{n_P}} \,} \right]\, = \,( - 3\,;\, - 5\,;\, - 4)\]
Ta có \[M\left( {0;2; - 6} \right) \in d\]. Vì \[d \subset \left( Q \right)\] \[ \Rightarrow M \in \left( Q \right)\]
Suy ra phương trình mặt phẳng \[\left( Q \right)\]là:
\[ - 3x\,\, - \,\,5(y\,\, - \,\,2)\,\, - \,\,4(z\,\, + \,\,6)\, = \,0\, \Leftrightarrow \,\, - 3x\, - \,\,5y\,\, - \,\,4z\,\, - \,\,14\,\, = \,\,0\]
Vậy
Chọn A
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp giải: Thiết diện qua trục của hình nón là một tam giác cân có cạnh đáy là đường kính đáy, hai cạnh bên là đường sinh của hình nón.
Diện tích xung quanh của hình nón bán kính đáy \[r\], đường sinh \[l\]được tính bởi công thức \[{S_{xq}} = \pi rl\]
Giải chi tiết:
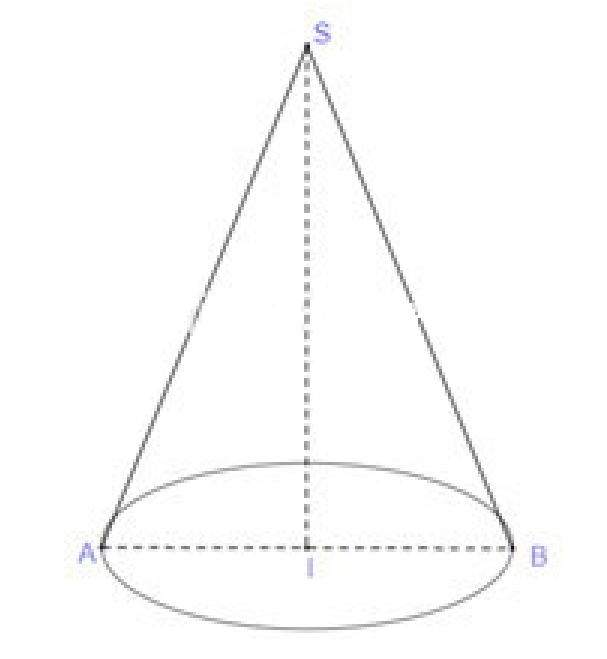
Gọi \[r\]là bán kính đáy và \[l\]là đường sinh của hình nón
Thiết diện qua trục của hình nón là một tam giác đều nên \[l = 2r\]
Do đó diện tích thiết diện là \[S = \frac{{{l^2}\sqrt 3 }}{4}\]
Theo bài ra ta có: \[\frac{{\sqrt 3 }}{4}.\,{l^2} = \,{a^3}\sqrt 3 \, \Rightarrow \,l\, = \,2a\, \Rightarrow \,r\, = \,a\]
Diện tích xung quanh của hình nón là: \[{S_{xq}} = \pi rl = \pi .a.2a = 2\pi {a^2}\]
Chọn C.
Câu 24:
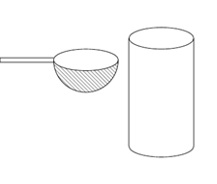
 Xem đáp án
Xem đáp án
Phương pháp giải: +) Tính thể tích của cái vá.
+) Tính thể tích của cái thùng hình trụ.
Giải chi tiết:
Thể tích của các vá là: \[V = \frac{1}{2}.\frac{4}{3}\pi {.3^3} = 18\pi \left( {c{m^3}} \right)\]
Thể tích của cái thùng hình trụ là \[V'\, = \,\pi \,{6^2}.\,10\, = \,360\pi \,\,\left( {c{m^3}} \right)\]
Vậy số lần đổ nước là \[\frac{{V'}}{V} = \frac{{360\pi }}{{18\pi }} = 20\](lần)
Chọn đáp án D.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Xác định góc giữa hai mặt phẳng \[\left( {ACC'A'} \right)\] và \[\left( {ABC} \right)\] Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính chiều cao và diện tích đáy của lăng trụ.
- Sử dụng công thức tính thể tích lăng trụ: \[{V_{lt}} = \,{S_{day}}.\,h\] trong đó \[{S_{day}}\] và \[h\] lần lượt là diện tích đáy và chiều cao của lăng trụ
Giải chi tiết:
Gọi \[D,E\]lần lượt là trung điểm \[AB,AC\]
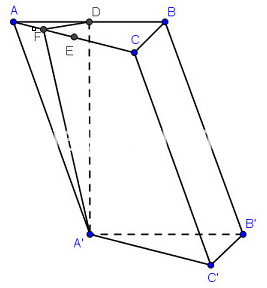
Vì tam giác \[ABC\]đều cạnh \[a\] nên \[BE \bot AC\]và \[BE = \frac{{a\sqrt 3 }}{2},{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]
Gọi \[F\]là điểm trên cạnh \[AC\]sao cho \[F\]là trung điểm \[AE\]ta có:
\[DF//BE\] (do \[DF\]là đường trung bình của tam giác \[ABE\]) mà \[BE \bot AC\]nên \[DF \bot AC\].
Ta có: \[\left\{ {\begin{array}{*{20}{c}}{AC \bot DF}\\{AC \bot A'D(A'D \bot (ABC))}\end{array} \Rightarrow AC \bot (DFA') \Rightarrow AC \bot A'F} \right.\]
Ta có: \[\left\{ {\begin{array}{*{20}{c}}{\left( {ACC'A'} \right) \cap \left( {ABC} \right) = AC}\\{\left( {ACC'A'} \right) \supset A'F \bot AC}\\{\left( {ABC} \right) \supset \,DF\, \bot \,AC}\end{array}} \right. \Rightarrow \angle \,\left( {\left( {ACC'A'} \right)\,;\,\left( {ABC} \right)} \right) = \,\angle \left( {A'F;DE} \right)\]
\[ \Rightarrow \angle DFA' = 45^\circ \, \Rightarrow \,\Delta DFA'\] vuông cân tại \[D\]
\[ \Rightarrow A'D = DF = \frac{1}{2}BE = \frac{1}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4}\]
\[ \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.A'D = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 3 }}{4} = \frac{{3{a^3}}}{{16}}\]
Chọn B.
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông với \(AB\, = \,AC\, = \,2\). Cạnh bên SA vuông góc với đáy và \(SA\, = \,3\). Gọi \(M\)là trung điểm của SC.
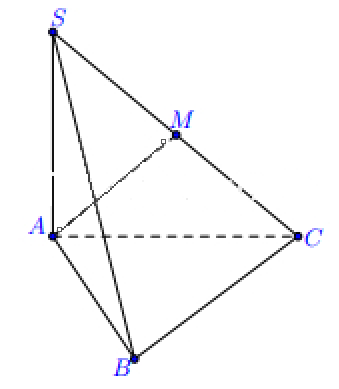
Tính khoảng cách giữa AM và BC.
 Xem đáp án
Xem đáp án
Phương pháp giải: - Sử dụng: khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường này đến mặt phẳng song song chứa đường thẳng kia
- Sử dụng: \({\left[ {\left( {\frac{1}{{{{(x - 1)}^2}}}} \right)} \right]^\prime }\) \(d\left( {S\,;\,\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}}\)
Giải chi tiết:
Gọi N là trung điểm của BC ta có MN // BC \( \Rightarrow \)BC // (AMN) \( \supset \)AM
\( \Rightarrow \)d (AM; BC) = d (BC; (AMN)) = d (C; (AMN))
Lại có: SC \( \cap \) (AMN) = M \( \Rightarrow \) \(\frac{{d(C;(AMN))}}{{d(S;(AMN))}} = \frac{{CM}}{{SM}} = 1\)
\( \Rightarrow d(C;(AMN)) = d(S;(AMN))\)
Ta có:
Gọi p là nửa chu vi tam giác AMN ta có
Vậy \( \Rightarrow d(AM;BC) = d(S;(AMN)) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}} = \frac{{3.\frac{1}{2}}}{{\frac{{\sqrt {22} }}{4}}} = \frac{{3\sqrt {22} }}{{11}}\)
Chọn C.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp giải:
Giải chi tiết:
Tâm I thuộc mặt phẳng \((xOy):z = 0\)nên ta có \(z = 0\). Suy ra giả sử \(I(x,y,0)\)
Mặt cầu \((S)\)qua \(A,B,C\)nên ta có \(IA = IB = IC = R\)
Ta có:
\(\left\{ \begin{array}{l}I{A^2}\, = \,I{B^2}\\I{B^2}\, = \,I{C^2}\end{array} \right.\, \Leftrightarrow \,\left\{ \begin{array}{l}{\left( {x\, - \,1} \right)^2}\, + \,{\left( {y\, - \,2} \right)^2}\, + \,{\left( 4 \right)^2}\, = \,{\left( {x\, - \,1} \right)^2}\, + \,{\left( {y\, + \,3} \right)^2}\, + \,{\left( { - 1} \right)^2}\\{\left( {x\, - \,1} \right)^2}\, + \,{\left( {y\, + \,3} \right)^2}\, + \,{\left( { - 1} \right)^2}\, = \,{\left( {x\, - \,2} \right)^2}\, + \,{\left( {y\, - \,2} \right)^2}\, + \,{\left( 3 \right)^2}\end{array} \right.\)
Vậy \(I( - 2,1,0)\)
Có \(IA\, = \,\sqrt {26} \, = \,R\)
Chọn B.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp giải: - với là 1 VTCP của đường thằng d; là 1 VTCP của mặt phẳng \((P)\)
- Đường thẳng đi qua \(M({x_0};{y_0};{z_0})\)và có 1 VTCP \[\overrightarrow u \,(a;b;c)\]có phương trình là: \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\)
Giải chi tiết:
Mặt phẳng \((P)\): \(2x - y + 2z - 5 = 0\)có 1 VTPT là
Gọi là 1 VTCP của đường thẳng d. Vì \(d \bot (P)\) \( \Rightarrow \) = = \((2; - 1;2)\)
Vậy phương trình đường thẳng d đi qua \(A(3;1; - 1)\)và có 1 VTCP là:
\(\frac{{x - 3}}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 1}}{2}\)
Chọn D.
Câu 29:
Cho hàm số \(y\, = \,f\left( x \right)\) liên tục trên \(\mathbb{R}\), có 3 cực trị và có đồ thị như hình vẽ.
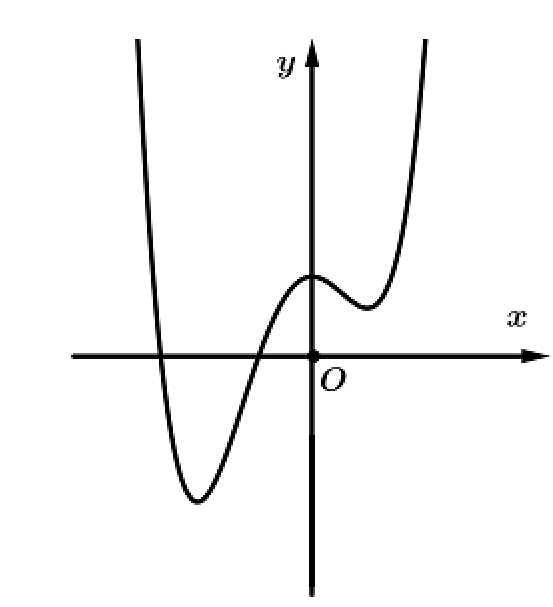
Tìm số điểm cực trị của hàm số \(y\, = \,f\left( {\frac{1}{{{{\left( {x\, - \,1} \right)}^2}}}} \right)\)
 Xem đáp án
Xem đáp án
Phương pháp giải: Tính \({\left[ {\left( {\frac{1}{{{{(x - 1)}^2}}}} \right)} \right]^\prime }\)và tìm số nghiệm bội lẻ, từ đó suy ra số cực trị
Giải chi tiết:
Ta có:
\[\begin{array}{l}g'(x)\, = \,{\left[ {f\,\left( {\frac{1}{{{{(x\, - \,1)}^2}}}} \right)} \right]^\prime } = {\left[ {\frac{1}{{{{(x\, - \,1)}^2}}}} \right]^\prime }.\,f'\left( {\frac{1}{{{{(x\, - \,1)}^2}}}} \right)\\ = \, - \frac{2}{{{{(x\, - \,1)}^3}}}.\,f'\left( {\frac{1}{{{{(x\, - \,1)}^2}}}} \right)\end{array}\]
\(g'(x) = 0 \Leftrightarrow f'\left( {\frac{1}{{{{(x - 1)}^2}}}} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{1}{{{{(x - 1)}^2}}} = {x_1} < 0(VN)}\\{\frac{1}{{{{(x - 1)}^2}}} = 0(VN)}\\{\frac{1}{{{{(x - 1)}^2}}} = {x_3} > 0}\end{array}} \right.\)
(nghiệm đơn)
Vậy hàm số đã cho có 2 điểm cực trị
Chọn D.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp giải: Gắn hệ trục tọa độ Oxyz để giải bài toán
Giải chi tiết:
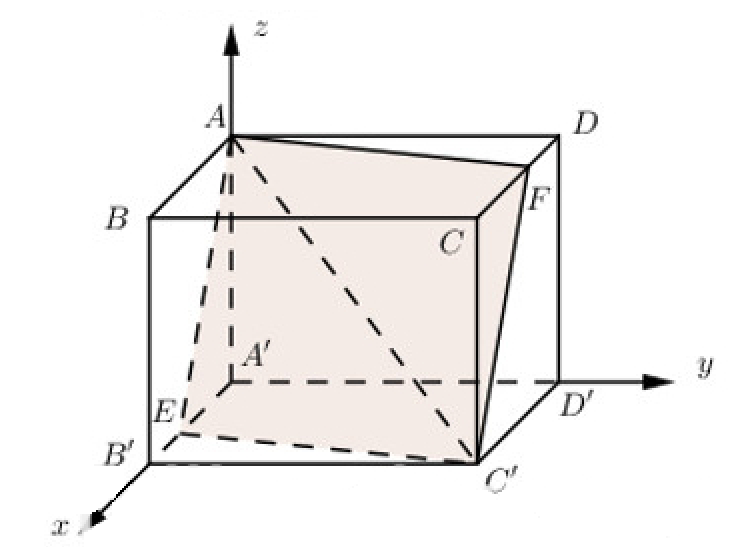
Giả sử mặt phẳng chứa AC’ cắt hình lập phương theo thiết diện là tứ giác AEC’F.
(\(E \in A'B';F \in CD\))
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{(AEC'F) \cap (ABCD) = AF}\\{(AEC'F) \cap (A'B'C'D') = AF//EC'}\\{(ABCD)//(A'B'C'D')}\end{array}} \right.\)
Tương tự ta chứng minh được AE // FC’
\( \Rightarrow \)AEC’F là hình bình hành \( \Rightarrow \) \({S_{AEC'F}}\, = \,2{S_{AEC'}}\)
Gắn hệ trục tọa độ như hình vẽ sao cho
A′(0;0;0); B′(2;0;0); C′(2;2;0); D′(0;2;0); A(0;0;2); B(2;0;2); A′(0;0;0); B′(2;0;0); C′(2;2;0); D′(0;2;0); A(0;0;2); B(2;0;2); C(2;2;2); D(0;2;2); C(2;2;2); D(0;2;2).
Gọi E(x;0;0) \((0 \le x \le 2)\)ta có:
Ta có: \[{x^2}\, - \,2x\, + \,4\, = \,\,{\left( {x\, - \,1} \right)^2}\, + \,3\, \ge \,3\, \Rightarrow \,{S_{ABC'}}\, \ge \,\frac{1}{2}\,\sqrt {8.\,3} \, = \,\sqrt 6 \]
Dấu bằng xảy ra \( \Leftrightarrow x = 1\), khi đó \({S_{AEC'\,\min }} = \,\sqrt 6 \, \Rightarrow \,{S_{AEC'F\,\min }}\, = \,2\sqrt 6 \)
Chọn D.
Câu 31:
Cho hàm số \(y\, = \,f\left( x \right)\) có đồ thị hàm số như hình.
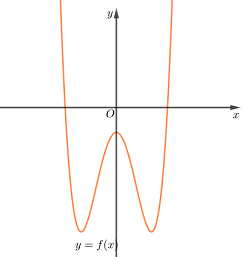
Hàm số \(y\, = \,\left| {f\left( {x\, + \,2018} \right)} \right|\) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Phương pháp giải: Dùng phép suy đồ thị, từ đồ thị hàm số \(y = f(x)\), vẽ đồ thị hàm số\(g(x) = f(x + 2018)\)bằng cách dịch chuyển đồ thị \(y = f(x)\)sang bên trái 2018 đơn vị
Vẽ đồ thị hàm số \(h(x) = \left| {g(x)} \right|\)bằng cách lấy đối xứng phần đồ thị \(g(x)\)phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó
Từ đồ thị hàm số \(y = h(x)\)suy ra số điểm cực trị của hàm \(y = h(x) = \left| {f(x + 2018)} \right|\)
Giải chi tiết:
Từ đồ thị hàm số đã cho, ta vẽ được các hàm số sau:
Vẽ đồ thị hàm số \(g(x) = f(x + 2018)\)bằng cách dịch chuyển đồ thị \(y = f(x)\)sang bên trái 2018 đơn vị
Lấy đối xứng phần đồ thị \(g(x)\)phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó ta được đồ thị của hàm số \(y = h(x) = \left| {g(x)} \right| = \left| {f(x + 2018)} \right|\)như hình vẽ dưới đây
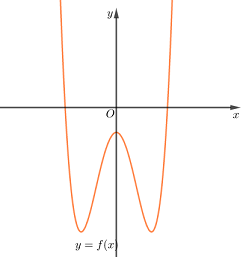
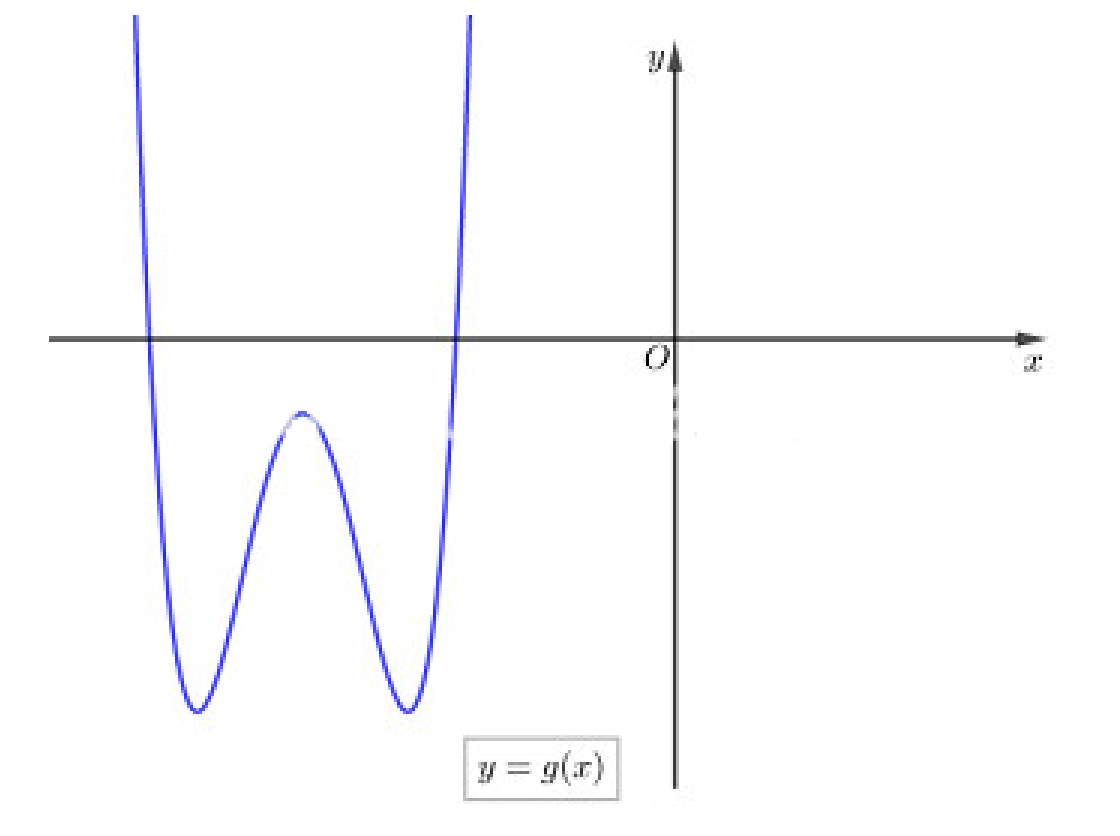
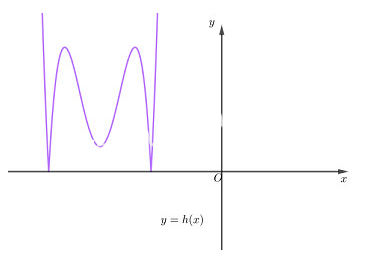
Từ đồ thị hàm số \(y\, = \,h(x)\)ta thấy đồ thị hàm số \(y\, = \,\left| {f(x\, + \,2018)} \right|\)có 5 điểm cực trị
Chọn A.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp giải: Chia cả 2 vế cho \({(x + 1)^2}\). Sử dụng phương pháp lấy nguyên hàm hai vế
Giải chi tiết: Ta có:
\(\begin{array}{l}2f(x) + ({x^2} - 1)f'(x) = \frac{{x{{(x + 1)}^2}}}{{\sqrt {{x^2} + 3} }}\\ \Leftrightarrow \frac{2}{{{{(x + 1)}^2}}}f(x) + \frac{{x - 1}}{{x + 1}}f'(x) = \frac{x}{{\sqrt {{x^2} + 3} }}\\ \Leftrightarrow {\left( {\frac{{x - 1}}{{x + 1}}} \right)^\prime }.f(x) + \frac{{x - 1}}{{x + 1}}.f'(x) = \frac{x}{{\sqrt {{x^2} + 3} }}\\ \Leftrightarrow {\left[ {\frac{{x - 1}}{{x + 1}}.f(x)} \right]^\prime } = \frac{x}{{\sqrt {{x^2} + 3} }}\end{array}\)
Lấy nguyên hàm hai vế ta được:
\(\int {{{\left[ {\frac{{x - 1}}{{x + 1}}.f(x)} \right]}^\prime }dx = \int {\frac{x}{{\sqrt {{x^2} + 3} }}dx} } \)
\( \Leftrightarrow \frac{{x - 1}}{{x + 1}}.f(x) = \int {\frac{x}{{\sqrt {{x^2} + 3} }}dx} \)
Đặt \(I = \int {\frac{x}{{\sqrt {{x^2} + 3} }}dx} \)
![]()
Khi đó ta có:
Thay \(x = 1\) ta có: \(0 = \,2\, + \,C\, \Leftrightarrow \,C\, = \, - 2\)
Thay \(x = 0\) ta có:
Chọn B.
Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp giải: Sử dụng phương pháp tích phân từng phần, đặt \(\left\{ {\begin{array}{*{20}{c}}{u = x + 2}\\{dv = f'(x)dx}\end{array}} \right.\)
Giải chi tiết:
Xét tích phân: \(I\, = \,\int\limits_0^2 {(x\, + \,2)f'(x)\,dx\, = \,8} \)
Đặt: \(\left\{ {\begin{array}{*{20}{c}}{u = x + 2}\\{dv = f'(x)dx}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{du = dx}\\{v = f(x)}\end{array}} \right.\) khi đó ta có:
\(I = (x\, + \,2)\,f(x)\left| {\begin{array}{*{20}{c}}2\\0\end{array}} \right.\, - \,\int\limits_0^2 {f(x)\,dx} \)
\(\begin{array}{l} \Rightarrow I\, = \,4\,f(2)\, - \,2f(0)\, - \,\int\limits_0^2 {f(x)\,dx} \\ \Rightarrow 8\, = \,5\, - \,\int\limits_0^2 {f(x)\,dx} \, \Rightarrow \,\int\limits_0^2 {f(x)\,dx} \, = \, - 3\end{array}\)
Chọn B.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp giải: - Tính số phần tử của không gian mẫu
- Gọi A là biến cố: “Số được chọn có đúng 2 chữ số chẵn”, số phần tử của A bằng số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ là \({\left( {C_4^2} \right)^2}.\,4!\) (bao gồm cả số có chữ số 0 đứng đầu)
- Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ trong đó bắt buộc chữ số 0 đứng đầu
- Tính xác suất của biến cố A: \(P(A) = \frac{{n(A)}}{{n(\Omega )}}\)
Giải chi tiết:
Gọi số tự nhiên có 4 chữ số là \(\overline {abcd} \)(\(a \ne 0\))
Không gian mẫu \(n(\Omega )\, = \,7.\,A_7^3\, = \,1470\)
Gọi A là biến cố: “số được chọn có đúng hai chữ số chẵn”
Chọn 2 chữ số chẵn trong các số 0, 1, 2, 3, 4, 5, 6, 7, có \(C_4^2\)cách, chọn 2 chữ số lẻ trong các số 0,1,2,3,4,5,6,7 có \(C_4^2\)cách
\( \Rightarrow \)số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ là \({\left( {C_4^2} \right)^2}.\,4!\) (bao gồm các số có chữ số 0 đứng đầu)
Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ trong đó bắt buộc có chữ số 0 đứng đầu là: \(C_3^1.\,C_4^2.\,3!\)
\(\begin{array}{l} \Rightarrow n(A)\, = \,{\left( {C_4^2} \right)^2}.\,4!\, - \,C_3^1.\,C_4^2.\,3!\, = \,756\\P(A)\, = \,\frac{{n(A)}}{{n(\Omega )}}\, = \,\frac{{756}}{{1470}}\, = \,\frac{{18}}{{35}}\end{array}\)
Chọn D.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp giải: Sử dụng phân chia thể tích
Sử dụng công thức tính thể tích hình chóp \(V = \frac{1}{3}h.S\), thể tích lăng trụ \(V = h.S\)
Giải chi tiết:
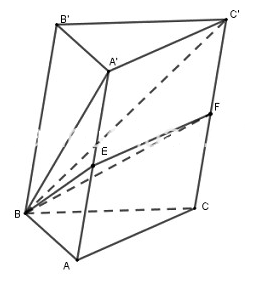
Ta có: \({V_{ABC.A'B'C'}}\, = \,d\left( {B\,;\,\left( {A'B'C'} \right)} \right).\,{S_{A'B'C'}}\, = \,V\)
\({V_{B.A'B'C'}}\, = \,\frac{1}{3}d\left( {B\,;\,\left( {A'B'C'} \right)} \right).\,{S_{A'B'C'}}\, = \,\frac{1}{3}V\)
Suy ra \({V_{B.AA'C'C}} = \,{V_{ABC.A'B'C'}}\, - \,{V_{B.A'B'C'}}\, - \,V\, - \,\frac{1}{3}V\, = \,\frac{2}{3}V\)
Lại có: \({S_{ACFE}} = \frac{1}{2}{S_{AA'C'C}}\) (do E,F lần lượt là trung điểm của \(AA',CC'\))
Suy ra \({V_{B.AEFC}} = \frac{1}{3}d\left( {B\,,\,\left( {AA'C'C} \right)} \right).\,SACFE\, = \,\frac{1}{3}d\left( {B\,,\,\left( {AA'C'C} \right)} \right).\,\frac{1}{2}{S_{AA'C'C}}\)
\( = \frac{1}{2}\,.\,\frac{1}{3}d\left( {B\,,\,\left( {AA'C'C} \right)} \right).\,{S_{AA'C'C}}\, = \,\frac{1}{2}{V_{B.AA'C'C}}\, = \frac{1}{2}.\frac{2}{3}V\, = \,\frac{1}{3}V\)
Suy ra \({V_{BEFA'B'C'}} = {V_{ABC.A'B'C'}} = V - \frac{1}{3}V = \frac{2}{3}V\)
Vậy tỉ số thể tích giữa hai phần là: \({V_{B.ACFE}}:{V_{BEFA'B'C'}} = \frac{1}{3}V:\frac{2}{3}V = 1:2\)
Chọn C.
Câu 36:
 Xem đáp án
Xem đáp án
Đáp án: y =-x-3
Phương pháp giải: Phương trình tiếp tuyến của đồ thị hàm số\(y = \,f(x)\)tại điểm \(M({x_0};{y_0})\) là:
\(y = \,f'(x)\,.\,(x - {x_0})\,\, + \,\,{y_0}\)
Giải chi tiết:
\(y = \frac{4}{{x - 1}}\), \(x \ne 1\)
Gọi \(M({x_0}\,;\,{y_0})\) là tiếp điểm có \({x_0}\)\( = \)\( - 1\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M({x_0};{y_0})\)là:
Câu 37:
Cho hàm số \(y\, = \,f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)là . Điểm cực đại của hàm số đã cho là:
 Xem đáp án
Xem đáp án
Đáp án: x=2
Phương pháp giải: Ta có: \(x = {x_0}\)là điểm cực trị của hàm số \(y = f(x)\)\( \Rightarrow f'({x_0}) = 0\)
Điểm \(x = {x_0}\)là điểm cực đại của hàm số \(y = f(x)\)\( \Leftrightarrow \)tại điểm \(x = {x_0}\)thì hàm số có\(y'\)đổi dấu từ dương sang âm
Lập bảng xét dấu của hàm số rồi chọn đáp án đúng
Giải chi tiết:
Ta có: \(f'(x) = 0\)
Lập bảng xét dấu:
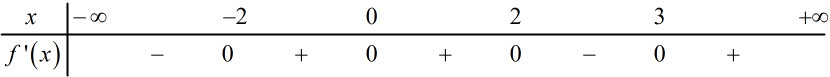
Dựa vào bảng xét dấu ta có: qua điểm \(x = 2\)thì \(f'(x)\)đổi dấu từ \( + \)sang \( - \)nên \(x = 2\)là điểm cực đại của hàm số
\( \Rightarrow \) hàm số có 1 điểm cực đại là \(x = 2\)
Câu 38:
Trong không gian với hệ trục tọa độ Oxyz, cho \(A\left( {1\,;\,2\,;\,3} \right),\,B\left( {3\,;\,4\,;\,4} \right)\). Tìm tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng \(2x\, + \,y\, + \,mz\, - \,1\, = \,0\)bằng độ dài đoạn thẳng AB.
 Xem đáp án
Xem đáp án
Đáp án: m = 2
Phương pháp giải: Công thức tính khoảng cách từ điểm \(M({x_0};{y_0};{z_0})\)đến mặt phẳng \((\alpha ):ax + by + cz + d = 0\)là\(d(M;(\alpha )) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Giải chi tiết:
Đặt \((\alpha ):2x + y + mz - 1 = 0\)
Ta có: \(d(A;(\alpha )) = \frac{{\left| {2.1 + 2 + 3.m - 1} \right|}}{{\sqrt {{2^2} + {1^2} + {m^2}} }} = \frac{{\left| {3 + 3m} \right|}}{{\sqrt {{m^2} + 5} }}\)
\(d(A;(\alpha )) = \)\(AB\)\( \Leftrightarrow \frac{{\left| {3 + 3m} \right|}}{{\sqrt {{m^2} + 5} }} = 3\)
Câu 39:
Chị bán hoa có 14 bông hoa hồng, trong đó có 6 bông màu đỏ, 5 bông màu hồng và 3 bông màu vàng. Trong ngày 20/11, bạn Lan chọn mua 4 bông hoa trong 14 bông hoa đó để tạo thành một bó hoa tặng cô giáo. Hỏi bạn Lan có bao nhiêu cách để có được bó hoa sao cho bó hoa không có quá hai màu hoa.
 Xem đáp án
Xem đáp án
Đáp án: 495 cách
Phương pháp giải: Sử dụng công thức tổ hợp và quy tắc tính phần bù để làm bài toán
Số cách bó hóa không quá hai màu hoa = số cách chọn bó hoa 4 bông bất kì – số cách chọn bó hoa có đủ 3 màu
Giải chi tiết:
Bó hoa không có quá hai màu hoa nên bạn Lan có thể chọn bó hoa có 1 màu hoặc có 2 màu.
Số cách chọn 4 bông hoa bất kì trong số 14 bông hoa là: \(C_{14}^4 = 1001\)cách
Số cách chọn 4 bông hoa đủ 3 màu như sau:
+) có 2 bông hoa đỏ, 1 bông vàng và 1 bông hồng: \(C_6^2.\,C_5^1.\,C_3^1\, = \,225\)cách chọn
+) có 1 bông hoa hồng, 1 bông hoa vàng và 1 bông hoa đỏ: \(C_6^1.\,C_5^2.\,C_3^1\, = \,180\)cách chọn
+)có 2 bông hoa vàng, 1 bông hoa hồng và 1 bông hoa đỏ: \(C_6^1.\,C_5^1.\,C_3^2\, = \,90\)cách chọn
\( \Rightarrow \)theo quy tắc cộng ta có: \(225 + 180 + 90 = 495\)cách chọn 4 bông hoa đủ cả 3 màu
Vậy có bông hoa không quá 2 màu
Câu 40:
Cho \(a\,,\,b\)là các số nguyên và . Tính \(P\, = \,{a^2}\, + \,{b^2}\, - \,a\, - \,b\).
 Xem đáp án
Xem đáp án
Đáp án: P = 320
Phương pháp giải: - Chia tử cho mẫu
- Sử dụng công thức \(\mathop {\lim }\limits_{x \to a} \left( {f(x) + g(x)} \right) = \mathop {\lim }\limits_{x \to a} f(x) + \mathop {\lim }\limits_{x \to a} f(x)\), lập hệ phương trình và giải hệ tìm a,b
- Thay giá trị a, b tìm được để tính giá trị biểu thức P
Giải chi tiết:
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{a{x^2} + bx - 5}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{a({x^2} - 1)\, + \,b(x - 1)\, + \,a\, + \,b\, - \,5}}{{x\, - \,1}}\\ = \mathop {\lim }\limits_{x \to 1} \left[ {a(x + 1) + b} \right]\,\, + \mathop {\,\lim }\limits_{x \to 1} \frac{{a\, + \,b\, - \,5}}{{x\, - \,1}}\\ = 2a\, + \,b\, + \,\mathop {\lim }\limits_{x \to 1} \frac{{a\, + \,b\, - \,5}}{{x\, - \,1}}\end{array}\)
Theo đề bài ta có:
\(\mathop {\lim }\limits_{x \to 1} \frac{{a{x^2}\, + \,bx\, - \,5}}{{x\, - \,1}}\, = \,20\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2a\, + \,b\, = \,20}\\{a\, + \,b\, - \,5\, = \,0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a\, = \,15}\\{b\, = \, - 10}\end{array}} \right.\)
Vậy
Câu 41:
Cho chuyển động xác định bởi phương trình \(S\, = \,{t^3}\, - \,3{t^2}\, - \,9t\), trong đó \(t\) được tính bằng giây và \(S\) được tính bằng mét. Tính vận tốc tại thời điểm gia tốc triệt tiêu.
 Xem đáp án
Xem đáp án
Đáp án: -12 m/s
Phương pháp giải: - Tính \({v_t} = {S'_t}\),\({a_t} = {v'_t}\)
- Tính thời điểm gia tốc triệt tiêu bằng cách giải phương trình \({a_t} = 0\)
- Tính vận tốc tại thời điểm \(t\)mới tìm được
Giải chi tiết:
\({v_t}\, = \,{S'_t}\, = \,3{t^2}\, - \,6t\, - \,9\)
\[ \Rightarrow \,{a_t}\, = \,{v'_t}\, = \,6t\, - \,6\]
Gia tốc triệt tiêu \( \Rightarrow \,{a_t}\, = \,0\)\( \Leftrightarrow \,6t\, - \,6\, = \,0\, \Leftrightarrow \,t\, = \,1\)
Câu 42:
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: Hàm đa thức bậc ba\(y = f(x)\)có hai điểm cực trị khi và chỉ khi phương trình \(f'(x) = 0\)có hai nghiệm phân biệt
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Ta có: \(f'(x) = {x^2} - 2mx + 10m - 25\)
Xét phương trình \(f'(x) = 0\)\( \Leftrightarrow {x^2} - 2mx + 10m - 25 = 0\)
Để hàm số ban đầu có 2 điểm cực trị thì phương trình \(f'(x) = 0\)có hai nghiệm phân biệt:
\(\begin{array}{l}\Delta ' = {m^2} - 10m + 25 > 0\\ \Leftrightarrow {(m - 5)^2} > 0\\ \Leftrightarrow m \ne 5\end{array}\)
Vậy
Câu 43:
 Xem đáp án
Xem đáp án
Đáp án: -2
Phương pháp giải: - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x),y = g(x)\), đường thẳng\(x = a,x = b\)là \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \). Từ đó tính diện tích 1 cánh của hình trang trí và suy ra diện tích hình trang trí
- Sử dụng dữ kiện diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\)diện tích mặt sàn suy ra 1 phương trình bậc nhất 2 ẩn\(a,b\)
- Sử dụng đồ thị hàm số \(y = a{x^3} + bx\)đi qua điểm \(A(1;1)\)suy ra thêm 1 phương trình bậc nhất 2 ẩn \(a,b\)
- Giải hệ tìm \(a,b\)và tính\(ab\)
Giải chi tiết:
Diện tích 1 cánh của hình trang trí là:
\( \Rightarrow \)diện tích hình trang trí là: \(S = 4{S_1} = \frac{4}{3} - a - 2b\)
Vì diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\)diện tích mặt sàn nên
Khi đó ta có:
Vậy
Câu 44:
Cho hàm số \(y\, = \,f\left( x \right)\) có bảng biến thiên:
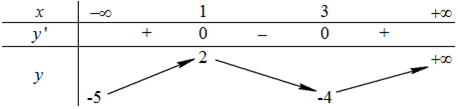
Tìm tất cả cá giá trị \(m\)để bất phương trình \(f\left( {\sqrt {x\, + \,1} \, + \,1} \right)\,\, \le \,\,m\)có nghiệm?
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: - Đặt ẩn phụ tìm điều kiện của \(t\)(\(t \in D\))
- Xét hàm \(f(t)\)và lập bảng biến thiên trên \(D\)
- Bất phương trình \(f(t) \le m\)có nghiệm nếu \(\mathop {\min f(t) \le m}\limits_D \)
Giải chi tiết:
Đặt thì \(t \in (1; + \infty )\). Với \(x = 3\) thì \(t = 3\)
Bảng biến thiên của \(f(t)\):
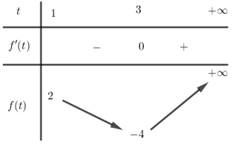
Do bất phương trình \(f(t) \le m\)có nghiệm khi và chỉ khi
Câu 45:
Xét các số phức \(z\) sao cho là số thực. Tập hợp các điểm biểu diễn của số phức \(z\) là:
 Xem đáp án
Xem đáp án
Đáp án: hai đường thẳng
Phương pháp giải: Giả sử \(z = x + yi\)\((x,y \in \mathbb{R})\), biến đổi và kết luận
Giải chi tiết:
Giả sử \(z = x + yi\)\((x,y \in \mathbb{R})\),ta có:
\((1 + x + yi)(1 - i(x + yi)) = (1 + x + yi)(1 + y - xi)\)
\( = (1 + x)(1 + y) + (y(1 + y) - x(1 + x))i + xy\)
Do \((1 + z)(1 - iz)\) là số thực nên
\(y(1 + y) - x(1 + x) = 0 \Leftrightarrow {\left( {x + \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - y = 0}\\{x + y + 1 = 0}\end{array}} \right.\)
Vậy tập hợp các điểm biểu diễn của số phức z là hai đường thẳng
Câu 46:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng \(a\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SA\, = \,a\sqrt 2 \)(hình bên). Gọi \(H\,,\,K\)lần lượt là hình chiếu vuông góc của \(A\) trên \(SB\,,\,SD\). Số đo của góc tạo bởi mặt phẳng \(\left( {AHK} \right)\) và \(\left( {ABCD} \right)\) bằng:
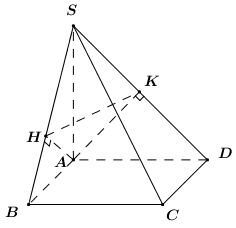
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: Sử dụng kết quả sau \(\left\{ {\begin{array}{*{20}{c}}{d \bot (P)}\\{d' \bot (Q)}\end{array}} \right. \Rightarrow \angle ((P);(Q)) = \angle (d;d')\)
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc
Giải chi tiết:
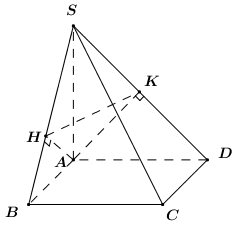
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\)
\(\left\{ {\begin{array}{*{20}{c}}{AH \bot SB}\\{AH \bot BC}\end{array}} \right. \Rightarrow AH \bot (SBC) \Rightarrow AH \bot SC\)
Chứng minh tương tự ta có: \(AK \bot (SCD) \Rightarrow AK \bot SC\)
\( \Rightarrow SC \bot (AHK)\)
Ta có: \(SA \bot (ABCD),SC \bot (AHK) \Rightarrow \angle ((AHK);(ABCD)) = \angle (SC;AC)\)
Vì \(ABCD\)là hình vuông cạnh \(a\)nên \(AC = a\sqrt 2 \). Lại có: \(SA\)= \(a\sqrt 2 \)nên \(\Delta SAC\)vuông cân tại \(A\)
Câu 47:
Trong không gian Oxyz, cho hai đường thẳng chéo nhau \(d\,:\,\left\{ \begin{array}{l}x\, = \,1\, + \,2t\\y\, = \, - 1\, - \,t\\z\, = \,1\end{array} \right.\) và \(d'\,:\,\frac{{x\, - \,2}}{{ - 1}}\, = \,\frac{{y\, + \,2}}{1}\, = \,\frac{{z\, - \,3}}{1}\). Khoảng cách giữa hai đường thẳng \(d\) và \(d'\,\)là:
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: Sử dụng công thức \(d(d;d') = \frac{{\left| {\left[ {\overrightarrow u \,,\,\overrightarrow {u'} } \right].\,\overrightarrow {MM'} } \right|}}{{\left| {\left[ {\overrightarrow u \,,\,\overrightarrow {u'} } \right]} \right|}}\)với \(\overrightarrow u \,,\,\overrightarrow {u'} \)lần lượt là VTCP của \(d\,,\,d'\), \(M \in d\) và \(M' \in d'\)
Giải chi tiết:
Đường thẳng đi qua điểm \(M(1; - 1; - 1)\)và có 1 VTCP \(\overrightarrow u \, = \,(2\,;\, - 1\,;\,0)\)
Đường thẳng \(d':\frac{{x - 2}}{{ - 1}} = \frac{{y + 2}}{1} = \frac{{z + 3}}{1}\)đi qua điểm \(M'(2; - 2; - 3)\)và có 1 VTCP \(\overrightarrow {u'} \, = \,( - 1\,;\,1\,;\,1)\)
\( \Rightarrow \left[ {\overrightarrow u \,,\,\overrightarrow {u'} } \right]\, = \,( - 1\,;\, - 2\,;\,1)\),
\( \Rightarrow \left[ {\overrightarrow u \,,\,\overrightarrow {u'} } \right].\,\overrightarrow {MM'} \, = \, - 1\, + \,2\, - \,2\, = \, - 1\)
Vậy
Câu 48:
Cho hàm số \(y\, = \,f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Hàm số \(y\, = \,f'\left( x \right)\) có bảng xét dấu như bảng bên dưới.
Bất phương trình \(f\left( x \right)\, > \,{e^{\cos x}}\, + \,m\) có nghiệm \(x\, \in \,\left( {0\,;\,\frac{\pi }{2}} \right)\) khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: - Cô lập \(m\)đưa bất phương trình về dạng \(g(x) \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Rightarrow m \le \mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
- Lập luận để chứng minh \(g(x)\)đơn điệu trên \(\left( {0;\frac{\pi }{2}} \right)\)và suy ra \(\mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
Giải chi tiết:
Ta có:
\(f(x) > {e^{\cos x}} + m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Leftrightarrow f(x) - {e^{\cos x}} \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
Đặt \(g(x) = f(x) - {e^{\cos x}}\) \( \Rightarrow g(x) \ge m\)có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\)
\( \Rightarrow m \le \mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} g\left( x \right)\)
Xét hàm số \(g(x) = f(x) - {e^{\cos x}}\)với \(x \in \left( {0;\frac{\pi }{2}} \right)\)ta có: \(g'(x) = f'(x) + \sin x.{e^{\cos x}}\)
Với \(x \in \left( {0;\frac{\pi }{2}} \right)\)ta có \(\sin x \in (0;1)\) \( \Rightarrow \sin x.{e^{\cos x}} > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Dựa vào BBT ta thấy \(f'(x) > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Do đó \(g'(x) > 0\forall x \in \left( {0;\frac{\pi }{2}} \right)\),do đó hàm số đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right]\)
\(\mathop { \Rightarrow \min g(x)}\limits_{\left[ {0;\frac{\pi }{2}} \right]} \) \( = g(0) = f(0) - e\)
\( \Rightarrow \mathop {\min g(x)}\limits_{\left( {0;\frac{\pi }{2}} \right)} \) \( > \mathop {\min g(x) = f(0) - e}\limits_{\left[ {0;\frac{\pi }{2}} \right]} \)
Vậy
Câu 49:
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng \(a\) và diện tích đáy bằng \({a^2}\) (tham khảo hình bên dưới). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng:
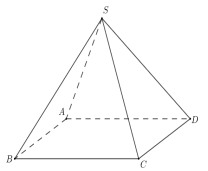
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: - Đổi \(d(A;(SBC))\)sang \(d(O;(SBC))\)với \(O = AC \cap BD\)
- Gọi \(M\)là trung điểm của \(BC\),trong \((SOM)\)kẻ \(OH \bot SM\)chứng minh \(OH \bot (SBC)\)
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách
Giải chi tiết:
Ta có: \(AO \cap (SBC) = C \Rightarrow \frac{{d(A;(SBC))}}{{d(O;(SBC))}} = \frac{{AO}}{{OC}} = 2\)
\( \Rightarrow d(A;(SBC)) = 2d(O;(SBC))\)
Gọi \(M\)là trung điểm của \(BC\),trong \((SOM)\)kẻ \(OH \bot SM\)ta có:
\(\left\{ {\begin{array}{*{20}{c}}{BC \bot OM}\\{BC \bot SO}\end{array}} \right. \Rightarrow BC \bot (SOM) \Rightarrow BC \bot OH\)
\(\left\{ {\begin{array}{*{20}{c}}{OH \bot BC}\\{OH \bot SM}\end{array}} \right. \Rightarrow OH \bot (SBC) \Rightarrow d(O;(SBC)) = OH\)
Vì \({S_{ABCD}} = {a^2} \Rightarrow BC = a,OM = \frac{1}{2}AB = \frac{1}{2}BC = \frac{a}{2}\)
Ta có:
Xét tam giác vuông \(SOM\): \(OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \frac{{\frac{{a\sqrt 2 }}{2}.\frac{a}{2}}}{{\sqrt {\frac{{{a^2}}}{2} + \frac{{{a^2}}}{4}} }} = \frac{{a\sqrt 6 }}{6}\)
Vậy
Câu 50:
Một thừa đất hình chữ nhật có chiều dài bằng 20 mét và chiều rộng bằng 10 mét, người ta giảm chiều dài \(x\) mét (với \(0\, < \,x\, < \,20\)) và tăng chiều rộng thêm 2x mét để được thửa đất mới. Tìm \(x\) để thửa đất mới có diện tích lớn nhất?
 Xem đáp án
Xem đáp án
Đáp án:
Phương pháp giải: - Tính chiều dài, chiều rộng mới của thửa đất sau đó tính diện tích mới của thửa đất
- Sử dụng phương pháp hàm số tìm GTLN
Giải chi tiết:
Chiều dài mới của thửa đất là \(20 - x\)(mét)
Chiều rộng của thửa đất là \(10 + 2x\) (mét)
Khi đó diện tích mới của thửa đất là \(S = (20 - x)(10 + 2x)\)
Ta có:
\(S' = 0 \Leftrightarrow x = \frac{{15}}{2}\)
Ta có BBT như sau:
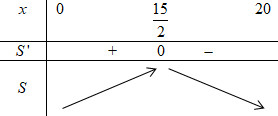
Vậy
Câu 51:
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 51 đến 55:
“Tây Tiến đoàn binh không mọc tóc
Quân xanh màu la dữ oai hùm
Mắt trừng gửi mộng qua biên giới
Đêm mơ Hà Nội dáng kiều thơm
Rải rác biên cương mồ viễn xứ
Chiến trường đi chẳng tiếc đời xanh
Áo bào thay chiếu anh về đất
Sông Mã gầm lên khúc độc hành
Tây Tiến người đi không hẹn ước
Đường lên thăm thẳm một chia phôi
Ai lên Tây Tiến mùa xuân ấy
Hồn về Sầm Nứa chẳng về xuôi”
(Trích Tây Tiến – Quang Dũng SGK Ngữ văn lớp 12, tập một)
Văn bản trên được viết theo thể thơ gì?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào thể thơ.
Giải chi tiết:
- Văn bản trên được viết theo thể thơ thất ngôn.
Chọn C.
Câu 52:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào bài Tây Tiến.
Giải chi tiết:
Nội dung cơ bản của 8 câu thơ đầu là: Văn bản tập trung khắc họa chân dung người chiến binh Tây Tiến (ngoại hình, tâm hồn, lí tưởng, sự hi sinh).
Chọn A.
Câu 53:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung đoạn trích.
Giải chi tiết:
Từ “Tây Tiến” được lặp lại ba lần trong đoạn thơ. Việc lặp lại ba lần từ “Tây Tiến” trong đoạn thơ cho ta hình dung nỗi nhớ Tây Tiến trong lòng nhà thơ là da diết, nó cứ trở đi trở lại trong lòng nhà thơ. Phép lặp này cũng cho chúng ta ấn tượng sâu sắc về hình ảnh trung tâm của nỗi nhớ trong lòng nhà thơ.
Chọn D.
Câu 54:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ biện pháp nói giảm, nói tránh.
Giải chi tiết:
Phép tu từ nói giảm được thể hiện trong câu thơ: “Áo bào thay chiếu anh về đất”. Cụm từ “về đất” được thay thế cho sự chết chóc, hi sinh.
Chọn B.
Câu 55:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào từ Hán Việt.
Giải chi tiết:
Văn bản có sử dụng rất nhiều từ Hán Việt đó là: đoàn binh, biên giới, chiến trường, biên cương, viễn xứ, áo bào, độc hành.
Chọn A.
Câu 56:
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
“Cái quý giá nhất trên đời mà mỗi người có thể góp phần mang lại cho chính mình và cho người khác đó là “năng lực tạo ra hạnh phúc”, bao gồm năng lực làm người, năng lực làm việc và năng lực làm dân.
Năng lực làm người là có cái đầu phân biệt được thiện - ác, chân - giả, chính - tà, đúng - sai..., biết được mình là ai, biết sống vì cái gì, có trái tim chan chứa tình yêu thương và giàu lòng trắc ẩn. Năng lực làm việc là khả năng giải quyết được những vấn đề của cuộc sống, của công việc, của chuyên môn, và thậm chí là của xã hội. Năng lực làm dân là biết được làm chủ đất nước là làm cái gì và có khả năng để làm được những điều đó. Khi con người có được những năng lực đặc biệt này thì sẽ thực hiện được những điều mình muốn.
Khi đó, mỗi người sẽ trở thành một “tế bào hạnh phúc”, một “nhà máy hạnh phúc” và sẽ ngày ngày “sản xuất hạnh phúc” cho mình và cho mọi người.
Xã hội mở ngày nay làm cho không có ai là “nhỏ bé” trên cuộc đời này, trừ khi tự mình muốn “nhỏ bé”. Ai cũng có thể trở thành những “con người lớn” bằng hai cách, làm được những việc lớn hoặc làm những việc nhỏ với một tình yêu cực lớn. Và khi biết chọn cho mình một lẽ sống phù hợp rồi sống hết mình và cháy hết mình với nó, mỗi người sẽ có được một hạnh phúc trọn vẹn. Khi đó, ta không chỉ có những khoảnh khắc hạnh phúc, mà còn có cả một cuộc đời hạnh phúc. Khi đó, tôi hạnh phúc, bạn hạnh phúc và chúng ta hạnh phúc. Đó cũng là lúc ta thực sự “chạm” vào hạnh phúc!.”
("Để chạm vào hạnh phúc"- Giản Tư Trung, Thời báo Kinh tế Sài Gòn Online, 3/2/2012)
Xác định phong cách ngôn ngữ của văn bản.
 Xem đáp án
Xem đáp án
Phương pháp giải:
Căn cứ vào các phong cách ngôn ngữ đã học.
Giải chi tiết:
- Phong cách ngôn ngữ của văn bản : Phong cách ngôn ngữ báo chí.
Chọn D.
Câu 57:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Nội dung chính của văn bản trên:
+ Con người có năng lực tạo ra hạnh phúc, bao gồm: năng lực làm người, làm việc, làm dân.
+ Để chạm đến hạnh phúc con người phải trở thành “con người lớn” bằng hai cách: làm việc lớn hoặc làm việc nhỏ với tình yêu lớn.
=> Con người tự tạo ra hạnh phúc bằng những vệc làm đúng đắn, phù hợp với yêu cầu của xã hội dù đó là việc lớn hay nhỏ.
Chọn D.
Câu 58:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung đoạn trích.
Giải chi tiết:
Công dụng của việc sử dụng dấu ngoặc kép: làm nổi bật, nhấn mạnh đến một ý nghĩa, một cách hiểu khác có hàm ý…
Chọn A.
Câu 59:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn trích.
Giải chi tiết:
Nghĩa hàm ý của từ “nhỏ bé”: tầm thường, thua kém, tẻ nhạt…
Chọn B.
Câu 60:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn trích.
Giải chi tiết:
Nghĩa hàm ý của từ “con người lớn”: tự do thể hiện mình, khẳng định giá trị bản thân, thực hiện những ước mơ, sống cao đẹp, có ích, có ý nghĩa…
Chọn B.
Câu 61:
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Nghệ thuật nói nhiều với tư tưởng nữa, nghệ thuật không thể nào thiếu tư tưởng. Không tư tưởng, con người có thể nào là con người. Nhưng trong nghệ thuật, tư tưởng từ ngay cuộc sống hằng ngày nảy ra, và thấm trong tất cả cuộc sống. Tư tưởng của nghệ thuật không bao giờ là trí thức trừu tượng một mình trên cao. Một câu thơ, một trang truyện, một vở kịch, cho đến một bức tranh, một bản đàn, ngay khi làm chúng ta rung động trong cảm xúc, có bao giờ để trí óc chúng ta nằm lười yên một chỗ… Cái tư tưởng trong nghệ thuật là một tư tưởng, yên lặng. Và cái yên lặng của một câu thơ lắng sâu xuống tư tưởng. Một bài thơ hay không bao giờ ta đọc qua một lần mà ta bỏ xuống được. Ta sẽ dừng tay trên trang giấy đáng lẽ lật đi và đọc lại bài thơ. Tất cả tâm hồn chúng ta đọc, không phải chỉ có trí thức. Và khác với cách độc riêng bằng trí thức, lần đọc thứ hai chậm hơn, đòi hỏi nhiều cố gắng hơn, nhiều chỗ chúng ta dừng lại hơn. Cho đến một câu thơ kia, người đọc nghe thì thầm mãi trong lòng, mắt không rời trang giấy.
(Trích Tiếng nói của Văn nghệ - Nguyễn Đình Thi, Ngữ văn 9, Tập 2 - NXB Giáo dục Việt Nam, 2015)
Ý nào sau đây KHÔNG được nói đến trong đoạn trích?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Tiếng nói của Văn nghệ.
Giải chi tiết:
Ý không được nói đến trong bài là: Phải có tư tưởng thì nghệ thuật mới có thế tồn tại được.
Chọn C.
Câu 62:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Tiếng nói của Văn nghệ.
Giải chi tiết:
Ý không nói đến cách thể hiện trong nghệ thuật với tư tưởng là: Tư tưởng của nghệ thuật là trí thức trừu tượng một mình trên cao.
Chọn A.
Câu 63:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ biện pháp tu từ.
Giải chi tiết:
Biện pháp tu từ: Nhân hóa: Cái tư tưởng - tư tưởng náu mình, yên lặng.
Chọn B.
Câu 64:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ các kiểu đoạn văn cơ bản: quy nạp, diễn dịch, tổng phân hợp, song hành, móc xích.
Giải chi tiết:
Đoạn trích trên được trình bày theo cách thức qui nạp đi từ các ý nhỏ đến ý lớn, từ các ý chi tiết đến ý khái quát, từ ý luận cứ cụ thể đến ý kết luận bao trùm.
Chọn A.
Câu 65:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Tiếng nói của Văn nghệ.
Giải chi tiết:
Đoạn văn trên bàn về nội dung: Tư tưởng trong nghệ thuật
Chọn D.
Câu 66:
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
…Khi tàu đông anh lỡ chuyến đi dài
Chỉ một người ở lại với anh thôi
Lúc anh vắng người ấy thường thức đợi
Khi anh khổ chỉ riêng người ấy tới
Anh yên lòng bên lửa ấm yêu thương
Người ấy chỉ vui khi anh hết lo buồn
Anh lạc bước, em đưa anh trở lại
Khi mệt mỏi thấy tháng ngày cằn cỗi
Em là sớm mai là tuổi trẻ của anh
Khi những điều giả dối vây quanh
Bàn tay ấy chở che và gìn giữ
Biết ơn em, em từ miền cát gió
Về với anh, bông cúc nhỏ hoa vàng […]
(Và anh tồn tại – Lưu Quang Vũ)
Xác định phương thức biểu đạt chính của văn bản trên.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào các phương thức biểu đạt đã học.
Giải chi tiết:
– Phương thức biểu đạt chính: biểu cảm
Chọn A.
Câu 67:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào phong cách ngôn ngữ đã học.
Giải chi tiết:
Phong cách ngôn ngữ nghệ thuật.
Chọn A.
Câu 68:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn trích.
Giải chi tiết:
Ý nghĩa của hình ảnh “bông cúc nhỏ hoa vàng”:
+ Là hình ảnh thiên nhiên đẹp.
+ Bông hoa cúc vàng nhỏ bé, yếu đuối, mong manh cần chở che.
+ Bông cúc vàng khiêm nhường giữa miền gió cát nhưng vẫn lặng lẽ dâng đời màu hoa đẹp nhất.
+ Đây là hình ảnh ẩn dụ chỉ vẻ đẹp của người phụ nữ. Bông cúc nhỏ khiêm nhường, thuỷ chung, nghĩa tình.
+ Lòng biết ơn trân trọng của nhà thơ với người phụ nữ yêu thương của mình.
Chọn D.
Câu 69:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào biện pháp tu từ.
Giải chi tiết:
- Biện pháp tu từ: điệp cấu trúc : “khi tàu đông; khi anh vắng; khi những điều…”
Chọn A.
Câu 70:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn trích.
Giải chi tiết:
- Nhân vật trữ tình “em” hiện lên trong đoạn thơ là người phụ nữ lặng thầm hi sinh hết mình vì người mình yêu, sống bao dung, vị tha. Tác giả thể hiện tấm lòng tri ân, yêu thương, trân trọng người phụ nữ mình yêu. Xem người phụ nữ ấy là báu vật, là “bông cúc nhỏ hoa vàng”, là “sớm mai tuổi trẻ”, là người bao dung, nhân hậu đã “chở che và gìn giữ”.
Chọn C.
Câu 71:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Thanh Thảo là một gương mặt đầy tâm huyết cho sự đổi mới thơ Việt. Bà đi tìm kiếm những nhân cách tài hoa, những nhân cách bất khuất, những suy nghĩ phóng khoáng, hay ông đến với những người vô danh, lặng thầm mà bất diệt.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Chữa lỗi dùng từ.
Giải chi tiết:
Thanh Thảo là một gương mặt đầy tâm huyết cho sự đổi mới thơ Việt. Ông đi tìm kiếm những nhân cách tài hoa, những nhân cách bất khuất, những suy nghĩ phóng khoáng, hay ông đến với những người vô danh, lặng thầm mà bất diệt.
Chọn C.
Câu 72:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Chữa lỗi dùng từ
Giải chi tiết:
Ông bà cha mẹ đã lao động vất vả, tạo ra thành quả để con cháu đời sau hưởng thụ.
Chọn D.
Câu 73:
Trong xã hội ta, không ít người sống ích kỉ, không giúp đỡ bao che cho người khác.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung câu.
Giải chi tiết:
Trong xã hội ta, không ít người sống ích kỉ, không giúp đỡ che chở cho người khác.
Chọn B.
Câu 74:
Phát biểu cảm nghĩ về một tác phẩm văn học (bài văn, bài thơ) là trình bày những cảm xúc, tưởng tượng, liên tưởng, suy ngẫm của mình về nội dung và giá trị của tác phẩm đó.
 Xem đáp án
Xem đáp án
Giải chi tiết:
Phát biểu cảm nghĩ về một tác phẩm văn học (bài văn, bài thơ) là trình bày những cảm xúc, tưởng tượng, liên tưởng, suy ngẫm của mình về nội dung và hình thức của tác phẩm đó.
Chọn A.
Câu 75:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Tùy bút là một thể văn. Tuy có chỗ gần với các thể bút kí, kí sự ở yếu tố miêu tả, ghi chép những hình ảnh, sự việc mà nhà văn quan sát, chứng kiến, nhưng tùy bút thiên về kể, chú trọng thể hiện cảm xúc, tình cảm, suy nghĩ của tác giả trước các hiện tượng và vấn đề của đời sống.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nghĩa của từ.
Giải chi tiết:
Tùy bút là một thể văn. Tuy có chỗ gần với các thể bút kí, kí sự ở yếu tố miêu tả, ghi chép những hình ảnh, sự việc mà nhà văn quan sát, chứng kiến, nhưng tùy bút thiên về biểu cảm, chú trọng thể hiện cảm xúc, tình cảm, suy nghĩ của tác giả trước các hiện tượng và vấn đề của đời sống.
Chọn B.
Câu 76:
 Xem đáp án
Xem đáp án
Phương pháp giải: Vận dụng kiến thức về nghĩa của từ.
Giải chi tiết:
- Các từ điểm yếu, khuyết điểm, nhược điểm: là cái mà bản thân mỗi người còn thiếu sót không hoàn hảo.
- Tù yếu điểm: điểm quan trọng, có ý nghĩa lớn lao nhất.
=> Từ yếu điểm không cùng nghĩa với từ còn lại.
Chọn C.
Câu 77:
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào từ loại.
Giải chi tiết:
- Đạo đức, kinh nghiệm, cách mạng là DT chỉ khái niệm.
- Mưa là DT chỉ hiện tượng.
=> Vậy từ “mưa” không cùng nhóm với các từ còn lại.
Chọn C.
Câu 78:
 Xem đáp án
Xem đáp án
Phương pháp giải: Vận dụng kiến thức về nghĩa của từ.
Giải chi tiết:
- Các từ phong ba , phong cảnh, cuồng phong: chỉ gió
- Tù phong cách: biểu hiện bên ngoài thái độ.
=> Từ phong cách không cùng nghĩa với từ còn lại.
Chọn C.
Câu 79:
 Xem đáp án
Xem đáp án
Giải chi tiết:
- Đặc điểm cơ bản của nền văn học Việt Nam từ năm 1945 đến năm 1975 là:
+ Nền văn học chủ yếu vận động theo hướng cách mạng hoá, gắn bó sâu sắc với vận mệnh chung của đất nước.
+ Nền văn học chủ yếu mang khuynh hướng sử thi và cảm hứng lãng mạn.
+ Nền văn học hướng về đại chúng.
Chọn B.
Câu 80:
 Xem đáp án
Xem đáp án
Phương pháp giải:Căn cứ vào Văn học hiện thực Việt Nam.
Giải chi tiết:
- Nhật kí trong tù, Tắt đèn, Chí Phèo thuộc văn học hiện thực
- Những sáng tác của nhóm Tự lực Văn đoàn thuộc trào lưu văn học lãng mạn
=> Vậy Những sáng tác của nhóm Tự lực Văn đoàn không cùng thể loại với tác phẩm còn lại.
Chọn D
Câu 81:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Sài Gòn là ________ trẻ trung, năng động, có nét hấp dẫn riêng về thiên nhiên và khí hậu. Người Sài Gòn có phong cách cởi mở, bộc trực, chân tình và trọng đạo nghĩa.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn.
Giải chi tiết:
Sài Gòn là thành phố trẻ trung, năng động, có nét hấp dẫn riêng về thiên nhiên và khí hậu. Người Sài Gòn có phong cách cởi mở, bộc trực, chân tình và trọng đạo nghĩa.
Chọn B.
Câu 82:
Cuộc Cách mạng tháng Tám có ý nghĩa ________đối với vận mệnh dân tộc.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung đoạn.
Giải chi tiết:
Sài Gòn là thành phố trẻ trung, năng động, có nét hấp dẫn riêng về thiên nhiên và khí hậu. Người Sài Gòn có phong cách cởi mở, bộc trực, chân tình và trọng đạo nghĩa.
Chọn B.
Câu 83:
Lao động là _______ thiêng liêng, là nguồn sống, nguồn hạnh phúc của mỗi người.
 Xem đáp án
Xem đáp án
Giải chi tiết:
Lao động là nghĩa vụ thiêng liêng, là nguồn sống, nguồn hạnh phúc của mỗi người.
Chọn B.
Câu 84:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Con đường hình thành bản sắc dân tộc của văn hóa không chỉ trông cậy vào sự tạo tác của chính dân tộc đó mà còn trông cậy vào ______ chiếm lĩnh, khả năng đồng hóa những giá trị văn hóa bên ngoài.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung câu văn.
Giải chi tiết:
Con đường hình thành bản sắc dân tộc của văn hóa không chỉ trông cậy vào sự tạo tác của chính dân tộc đó mà còn trông cậy vào khả năng chiếm lĩnh, khả năng đồng hóa những giá trị văn hóa bên ngoài.
Chọn B.
Câu 85:
Tố Hữu từng quan niệm “Thơ là chuyện______. [...] Thơ là tiếng nói đồng ý và đồng tình, tiếng nói đồng chí.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào nội dung câu văn.
Giải chi tiết:
Tố Hữu từng quan niệm “Thơ là chuyện đồng điệu. [...] Thơ là tiếng nói đồng ý và đồng tình, tiếng nói đồng chí.
Chọn A.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Từ ấy trong tôi bừng nắng hạ
Mặt trời chân lí chói qua tim
Hồn tôi là một vườn hoa lá
Rất đậm hương và rộn tiếng chim...
(Trích Từ ấy – Tố Hữu, Ngữ văn 11, NXB Giáo dục)
Biện pháp tu từ được sử dụng trong hai câu thơ:
"Từ ấy trong tôi bừng nắng hạ
Mặt trời chân lý chói qua tim"
 Xem đáp án
Xem đáp án
Giải chi tiết:
liên tưởng tới một đối tượng khác có nhiều nét tương đồng. Trong đoạn thơ, nắng hạ và mặt trời chân lí ngầm chỉ ánh sáng của lí tưởng cách mạng.
- Cho thấy niềm vui sướng và hạnh phúc của tác giả khi được chiến đấu dưới ngọn cờ của Đảng
Chọn C.
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
“Tỉnh dậy hắn thấy già mà vẫn còn cô độc. Buồn thay cho đời! Có lý nào như thế được? Hắn đã già rồi hay sao? Ngoài bốn mươi tuổi đầu... Dẫu sao, đó không phải tuổi mà người ta mới bắt đầu sửa soạn. Hắn đã tới cái dốc bên kia của đời. Ở những người như hắn, chịu đựng biết bao nhiêu là chất độc, đầy đọa cực nhọc mà chưa bao giờ ốm, một trận ốm có thể gọi là dấu hiệu báo rằng cơ thể đã hư hỏng nhiều. Nó là một cơn mưa gió cuối thu cho biết trời gió rét, nay mùa đông đã đến. Chí Phèo hình như đã trông thấy trước tuổi già của hắn, đói rét và ốm đau, và cô độc, cái này còn đáng sợ hơn đói rét và ốm đau.”
(Trích đoạn trích Chí Phèo, Nam Cao, SGK Ngữ văn lớp 11, tập 1)
Xác định biện pháp tu từ được sử dụng trong câu Hắn đã tới cái dốc bên kia của đời.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào các biện pháp tu từ.
Giải chi tiết:
- Biện pháp ẩn dụ.
Chọn C.
Câu 88:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Trong những dòng sông đẹp ở các nước mà tôi thường nghe nói đến, hình như chỉ sông Hương là thuộc về một thành phố duy nhất. Trước khi về đến vùng châu thổ êm đềm, nó đã là một bản trường ca của rừng già, rầm rộ giữa bóng cây đại ngàn, mãnh liệt qua những ghềnh thác, cuộn xoáy như cơn lốc vào những đáy vực bí ẩn, và cũng có lúc nó trở nên dịu dàng và say đắm giữa những dặm dài chói lọi màu đỏ của hoa đỗ quyên rừng. Giữa dòng Trường Sơn, sông Hương đã sống một nửa cuộc đời của mình như một cô gái Di-gan phóng khoáng và man dại. Rừng già đã hun đúc cho nó một bản lĩnh gan dạ, một tâm hồn tự do và trong sáng. Nhưng chính rừng già nơi đây, với cấu trúc đặc biệt có thể lí giải được về mặt khoa học, đã chế ngự sức mạnh bản năng ở người con gái của mình để khi ra khỏi rừng, sông Hương nhanh chóng mang một sắc đẹp dịu dàng và trí tuệ, trở thành người mẹ phù sa của một vùng văn hóa xứ sở. Nếu chỉ mải mê nhìn ngắm khuôn mặt kinh thành của nó, tôi nghĩ rằng người ta sẽ không hiểu một cách đầy đủ bản chất của sông Hương với cuộc hành trình đầy gian truân mà nó đã vượt qua, không hiểu thấu phần tâm hồn sâu thẳm của nó mà dòng sông hình như không muốn bộc lộ, đã đóng kín lại ở cửa rừng và ném chìa khóa trong những hang đá dưới chân núi Kim Phụng.
(Trích Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường, Ngữ văn 12, Tập một, NXB Giáo dục)
Dòng sông được hiện lên như thế nào qua đoạn văn?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung đoạn trích.
Giải chi tiết:
- Dòng sông được hiện lên với vẻ độc đáo:
+ Dòng chảy phong phú: vừa mãnh liệt vừa dịu dàng, say đắm
+ Dòng sông mang vẻ đẹp nữ tính: từ cô gái di-gan đến người mẹ phù sa
+ Dòng sông mang vẻ đẹp kín đáo với tâm hồn sâu thẳm
Chọn B.
Câu 89:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Tôi buộc lòng tôi với mọi người
Để tình trang trải với trăm nơi
Để hồn tôi với bao hồn khổ
Gần gũi nhau thêm mạnh khối đời.
(Trích Từ ấy – Tố Hữu, Ngữ văn 12, Tập một, NXB Giáo dục)
Biện pháp tu từ được sử dụng trong hình ảnh trăm nơi.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ biện pháp tu từ.
Giải chi tiết:
Biện pháp tu từ được sử dụng trong hình ảnh "trăm nơi" đó là biện pháp tu từ hoán dụ chỉ mọi người sống ở khắp nơi. Tác giả muốn tình yêu của mình được hòa cùng tình yêu của muôn người. Đó là tình yêu to lớn, tình yêu gắn bó. Tình yêu đó bao la và rộng lớn.
Chọn B.
Câu 90:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Lúc ấy đã khuya. Trong nhà ngủ yên. Mị trở dậy thổi lửa, ngọn lửa bập bùng sáng lên. Mị trông sang thấy hai mắt A Phủ cũng vừa mở. Dòng nước mắt lấp lánh bò xuống hai hõm má đã xám đen. Thấy tình cảnh thế, Mị chợt nhớ đêm năm trước, A Sử trói Mị, Mị cũng phải trói đứng thế kia. Nước mắt chảy xuống miệng, xuống cổ, không biết lau đi được. Trời ơi nó bắt trói đứng người ta đến chết. Nó bắt mình chết cũng thôi. Nó đã bắt trói đến chết người đàn bà ngày trước ở cái nhà này. Chúng nó thật độc ác. Chỉ đêm mai là người kia chết, chết đau, chết đói, chết rét, phải chết. Ta là thân đàn bà, nó đã bắt về trình ma rồi, chỉ còn biết đợi ngày rũ xương ở đây thôi... Người kia việc gì mà phải chết. A Phủ... Mị phảng phất nghĩ như vậy.
(Trích Vợ chồng A Phủ - Tô Hoài, Ngữ văn 12, Tập hai, NXB Giáo dục)
Hình ảnh “giọt nước mắt” trong đoạn trích trên có tác dụng gì?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung đoạn trích
Giải chi tiết:
Hình ảnh “giọt nước mắt” trong đoạn trích trên có tác dụng:
Là sợi dây kết nối sự đồng cảm trong Mị từ đó khơi dậy sức mạnh tiề
Chọn B.
Câu 91:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Bèo dạt về đâu, hàng nối hàng;
Mênh mông không một chuyến đò ngang.
Không cầu gợi chút niềm thân mật,
Lặng lẽ bờ xanh tiếp bãi vàng.
(Tràng Giang– Huy Cận, Ngữ văn 11, Tập một, NXB Giáo dục)
Cái cảm giác trống trải, xa vắng của không gian “tràng giang” trong khổ thơ thứ ba, chủ yếu được tô đậm bởi yếu tố nghệ thuật nào?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ biện pháp tu từ.
Giải chi tiết:
- Từ phủ định: “Không đò… không cầu...”
- Điệp từ: không
Chọn C.
Câu 92:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Sự thật là từ mùa thu năm 1940, nước ta đã thành thuộc địa của Nhật, chứ không phải thuộc địa của Pháp
nữa. Khi Nhật hàng Đồng minh thì nhân dân cả nước ta đã nổi dậy giành chính quyền lập nên nước Việt
Nam Dân chủ Cộng hòa.
(Trích Tuyên ngôn độc lập của Hồ Chí Minh, SGK Ngữ văn lớp 12, tập 1)
Xác định biện pháp tu từ được sử dụng trong đoạn trích.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào biện pháp tu từ.
Giải chi tiết:
- Biện pháp tu từ được sử dụng trong đoạn trích là: Điệp từ (sự thật) với tác dụng khẳng định, nhấn mạnh quyền độc lập tự do của dân tộc Việt Nam
Chọn B.
Câu 93:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như
có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ...Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại... Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng "Đi đi..." rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Xác định ý nghĩa nghệ thuật của hình ảnh cái cọc và dây mây trong văn bản ?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ bài Vợ chồng A Phủ.
Giải chi tiết:
Ý nghĩa nghệ thuật của hình ảnh cái cọc và dây mây trong văn bản:
- Ý nghĩa tả thực: nơi để trói và dụng cụ để trói A Phủ của thống lí Pá Tra để đổi mạng nửa con bò bị hổ ăn thịt.
- Ý nghĩa tượng trưng: Biểu tượng cho cái ác, cái chết do bọn chúa đất miền núi gây ra. Đó cũng là nơi không hẹn mà gặp giữa hai thân phận đau khổ cùng cảnh ngộ. Đó cũng là nơi để Mị bộc lộ tình thương người và đi đến quyết định táo bạo giải cứu A Phủ cũng là giải thoát cuộc đời mình. Sự sống, khát vọng tự do tỏa sáng từ trong cái chết.
Chọn C.
Câu 94:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Em ơi em Đất Nước là máu xương của mình20
Phải biết gắn bó và san sẻ
Phải biết hóa thân cho dáng hình xứ sở
Làm nên Đất Nước muôn đời...
(Trích đoạn trích Đất Nước của Nguyễn Khoa Điềm, SGK Ngữ văn lớp 12, tập 1)
Từ "hóa thân" trong đoạn thơ trên có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung tác phẩm.
Giải chi tiết:
Ý chính của đoạn thơ : thể hiện niềm suy tư, trăn trở của người phụ nữ trong tình yêu
Chọn D.
Câu 95:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Mơ khách đường xa, khách đường xa
Áo em trắng quá nhìn không ra
Ở đây sương khói mờ nhân ảnh
Ai biết tình ai có đậm đà ?
(Trích Đây thôn Vĩ Dạ – Hàn Mặc Tử, Ngữ văn 11, Tập hai, NXB Giáo dục)
Câu thơ: Ai biết tình ai có đậm đà? có mấy cách hiểu?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Căn cứ vào nội dung tác phẩm.
Giải chi tiết:
Câu thơ : Ai biết tình ai có đậm đà ?
Hai cách hiểu :
- Ai có biết chăng tình cảm ( Hàn Mặc Tử ) vẫn đậm đà với con người và cảnh vật Vĩ Dạ.
- Ai mà biết được tình cảm của ai đó với ai có đậm đà hay không ?
Chọn B.
Câu 96:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Từ ấy trong tôi bừng nắng hạ
Mặt trời chân lý chói qua tim
Hồn tôi là một vườn hoa lá
Rất đậm hương và rộn tiếng chim
(Từ ấy – Tố Hữu, Ngữ văn 11, Tập hai, NXB Giáo dục)
Dòng nào dưới đây nêu đúng nhất nội dung đoạn trích trên:
 Xem đáp án
Xem đáp án
Phương pháp giải: Vận dụng kiến thức đã học trong bài Từ ấy.
Giải chi tiết:
Khổ thơ trên là khổ thơ thứ nhất trong bài thơ Từ ấy của nhà thơ Tố Hữu. Bài thơ đánh dấu bước ngoặt của nhà tho khi ông tìm thấy ánh sáng của lý tưởng cách mạng. Khổ thơ đầu tiên thể hiện tâm trạng vui tươi, say mê khi được giác ngộ lý tưởng của tác giả.
Chọn C.
Câu 97:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
- Mình về mình có nhớ ta?
Mười lăm năm ấy thiết tha mặn nồng.
Mình về mình có nhớ không
Nhìn cây nhớ núi, nhìn sông nhớ nguồn?
Tiếng ai tha thiết bên cồn
Bâng khuâng trong dạ, bồn chồn bước đi
Áo chàm đưa buổi phân ly
Cầm tay nhau biết nói gì hôm nay...
(Trích Việt Bắc – Tố Hữu, Ngữ văn 12, Tập một, NXB Giáo dục)
Nêu ý nghĩa tu từ của các từ láy trong đoạn thơ.
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào từ láy.
Giải chi tiết:
Ý nghĩa tu từ của từ láy: thiết tha, tha thiết, bâng khuâng,.. trong đoạn thơ đã diễn tả con sóng lòng đang dấy lên trong tâm hồn nhà thơ lúc phân ly.
Chọn A.
Câu 98:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Ôi con sóng ngày xưa
Và ngày sau vẫn thế
Nỗi khát vọng tình yêu
Bồi hồi trong ngực trẻ
(Trích Sóng – Xuân Quỳnh - Ngữ văn 12, Tập một, NXB Giáo dục)
Chỉ ra biện pháp tu từ được sử dụng trong hai câu thơ cuối đoạn trích
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ vào biện pháp tu từ.
Giải chi tiết:
- Biện pháp tu từ được sử dụng trong hai câu thơ cuối: ẩn dụ (ngực trẻ).
Chọn A.
Câu 99:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Lúc ấy đã khuya. Trong nhà ngủ yên. Mị trở dậy thổi lửa, ngọn lửa bập bùng sáng lên. Mị trông sang thấy hai mắt A Phủ cũng vừa mở. Dòng nước mắt lấp lánh bò xuống hai hõm má đã xám đen. Thấy tình cảnh thế, Mị chợt nhớ đêm năm trước, A Sử trói Mị, Mị cũng phải trói đứng thế kia. Nước mắt chảy xuống miệng, xuống cổ, không biết lau đi được. Trời ơi nó bắt trói đứng người ta đến chết. Nó bắt mình chết cũng thôi. Nó đã bắt trói đến chết người đàn bà ngày trước ở cái nhà này. Chúng nó thật độc ác. Chỉ đêm mai là người kia chết, chết đau, chết đói, chết rét, phải chết. Ta là thân đàn bà, nó đã bắt về trình ma rồi, chỉ còn biết đợi ngày rũ xương ở đây thôi... Người kia việc gì mà phải chết. A Phủ... Mị phảng phất nghĩ như vậy.
(Trích Vợ chồng A Phủ - Tô Hoài, Ngữ văn 12, Tập hai, NXB Giáo dục)
Hình ảnh “giọt nước mắt” trong đoạn trích trên có tác dụng gì?
 Xem đáp án
Xem đáp án
Phương pháp giải: Căn cứ nội dung đoạn trích.
Giải chi tiết:
Hình ảnh “giọt nước mắt” trong đoạn trích trên có tác dụng:
Là sợi dây kết nối sự đồng cảm trong Mị từ đó khơi dậy sức mạnh tiề
Chọn B.
Câu 100:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Hỡi đồng bào cả nước,
Tất cả mọi người đều sinh ra có quyền bình đẳng. Tạo hóa cho họ những quyền không ai có thể xâm phạm được; trong những quyền ấy, có quyền được sống, quyền tự do và quyền mưu cầu hạnh phúc".
Lời bất hủ ấy ở trong bản Tuyên ngôn Độc lập năm 1776 của nước Mỹ. Suy rộng ra, câu ấy có ý nghĩa là: tất cả các dân tộc trên thế giới đều sinh ra bình đẳng, dân tộc nào cũng có quyền sống, quyền sung sướng và quyền tự do.
Bản Tuyên ngôn Nhân quyền và Dân quyền của Cách mạng Pháp năm 1791 cũng nói: Người ta sinh ra tự do và bình đẳng về quyền lợi; và phải luôn luôn được tự do và bình đẳng về quyền lợi.
Đó là những lẽ phải không ai chối cãi được.
(Trích Tuyên ngôn độc lập của Hồ Chí Minh, SGK Ngữ văn lớp 12, tập 1)
Phương thức biểu đạt chính trong đoạn trích là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải:
Căn cứ các phương thức biểu đạt đã học.
Giải chi tiết:
Phương thức biểu đạt nghị luận
Chọn B.Câu 101:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 102:
 Xem đáp án
Xem đáp án
Chọn C
Câu 103:
 Xem đáp án
Xem đáp án
Chọn A
Câu 105:
 Xem đáp án
Xem đáp án
Chọn B
Câu 106:
 Xem đáp án
Xem đáp án
Chọn A
Câu 107:
 Xem đáp án
Xem đáp án
Chọn C
Câu 108:
 Xem đáp án
Xem đáp án
Chọn D
Câu 109:
Dựa vào thông tin dưới đây để trả lời các câu từ 109 đến 110:
Thế kỉ XXI sẽ tiếp tục có nhiều biến đổi. Khoa học và công nghệ sẽ có bước tiến nhảy vọt. Kinh tế tri
thức có vai trò ngày càng nổi bật trong quá trình phát triển lực lượng sản xuất. Toàn cầu hóa kinh tế là một xu thế khách quan, lôi cuốn ngày càng nhiều nước tham gia; xu thế này đang bị một số nước phát triển và các tập đoàn kinh tế tư bản xuyên quốc gia chi phối, chứa đựng nhiều mâu thuẫn, vừa có mặt tích cực vừa có mặt tiêu cực, vừa có hợp tác vừa có đấu tranh. Các mâu thuẫn cơ bản trên thế giới biểu hiện dưới những hình thức và mức độ khác nhau vẫn tồn tại và phát triển, có mặt sâu sắc hơn. Thế giới đứng trước nhiều vấn đề toàn cầu mà không một quốc gia riêng lẻ nào có thể tự giải quyết nếu không có sự hợp tác đa phương như: bảo vệ môi trường, hạn chế sự bùng nổ về dân số, đẩy lùi những dịch bệnh hiểm nghèo, chống tội phạm quốc tế, …
Trong một vài thập kỉ tới, ít có khả năng xảy ra chiến tranh thế giới. Nhưng chiến tranh cục bộ, xung đột vũ trang, xung đột dân tộc, tôn giáo, chạy đua vũ trang, hoạt động can thiệp lật đổ, khủng bố còn xảy ra ở nhiều nơi với tính chất phức tạp ngày càng tăng. Hòa bình, hợp tác và phát triển là xu thế lớn, phản ánh đòi hỏi bức xúc của các quốc gia, dân tộc. Cuộc đấu tranh vì hòa bình, độc lập, dân chủ, dân sinh, tiến bộ và công bằng xã hội sẽ có những bước tiến mới. Khu vực Đông Nam Á, châu Á - Thái Bình Dương sau khủng hoảng tài chính - kinh tế có khả năng phát triển năng động nhưng vẫn tiềm ẩn những nhân tố gây mất ổn định.
Những nét mới ấy trong tình hình thế giới và khu vực có tác động mạnh mẽ đến tình hình nước ta. Trước mắt nhân dân ta có cả cơ hội lớn và thách thức lớn.
(Đảng Cộng sản Việt Nam, Văn kiện Đại hội đại biểu toàn quốc lần thứ IX, NXB CTQG, H., 2001, tr 64 65)
Ảnh hưởng của chủ nghĩa li khai, chủ nghĩa khủng bố đến xu thế phát triển của thế giới ngày nay là
 Xem đáp án
Xem đáp án
Chọn B
Câu 110:
 Xem đáp án
Xem đáp án
Chọn D
Câu 112:
 Xem đáp án
Xem đáp án
Chọn C
Câu 114:
 Xem đáp án
Xem đáp án
Chọn A
Câu 115:
 Xem đáp án
Xem đáp án
Chọn C
Câu 116:
Cho bảng số liệu: Diện tích và sản lượng lúa của một số tỉnh năm 2017
(Nguồn: Niên giám thống kê Việt Nam 2014, MAH Thổng lẻ 2019).
Theo bảng số liệu, nhận xét nào sau đây đúng khi so sánh năng suất lúa của các tỉnh năm 2018?
 Xem đáp án
Xem đáp án
Chọn A
Câu 117:
 Xem đáp án
Xem đáp án
Chọn C
Câu 119:
 Xem đáp án
Xem đáp án
Chọn B
Câu 120:
 Xem đáp án
Xem đáp án
Chọn D
Câu 121:
 Xem đáp án
Xem đáp án
Chọn C
Câu 122:
 Xem đáp án
Xem đáp án
Chọn C
Câu 123:
 Xem đáp án
Xem đáp án
Chọn D
Câu 124:
 Xem đáp án
Xem đáp án
Chọn C
Câu 125:
 Xem đáp án
Xem đáp án
Chọn B
Câu 126:
 Xem đáp án
Xem đáp án
Chọn D
Câu 127:
 Xem đáp án
Xem đáp án
Chọn A
Câu 128:
Bức xạ anpha, beta và gamma
1. có khả năng đâm xuyên khác nhau qua vật chất.
2. bị lệch khác nhau trong điện trường.
3. bị lệch khác nhau trong từ trường.
Dưới đây là các sơ đồ minh họa:
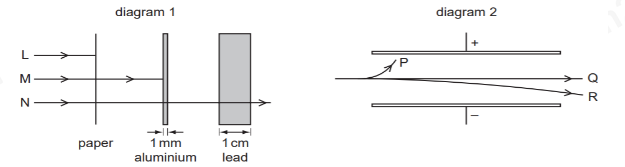
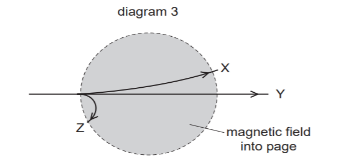
Ba kí hiệu trên sơ đồ cho kết quả của cùng một loại bức xạ là
 Xem đáp án
Xem đáp án
Chọn C
Câu 129:
 Xem đáp án
Xem đáp án
Chọn C
Câu 130:
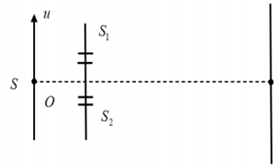
 Xem đáp án
Xem đáp án
Câu 131:
Nung 13,44 lít (đktc) hỗn hợp X gồm axetilen, propilen và hiđro (tỉ lệ mol 2 : 1 : 3) trong bình đựng bột Ni. Sau một thời gian thu được hỗn hợp khí Y có tỉ khối hơi so với X là 1,5. Dẫn toàn bộ Y qua bình đựng dung dịch AgNO3 trong NH3 thì thu được 12 gam kết tủa và hỗn hợp khí Z. Hấp thụ hết Z vào bình đựng dung dịch brom dư thì thấy có m gam brom phản ứng. Giá trị của m là
 Xem đáp án
Xem đáp án
Chọn B
Câu 132:
 Xem đáp án
Xem đáp án
Chọn B
Câu 133:
 Xem đáp án
Xem đáp án
Chọn C
Câu 134:
 Xem đáp án
Xem đáp án
Chọn A
Câu 135:
Cho thí nghiệm như hình vẽ sau:
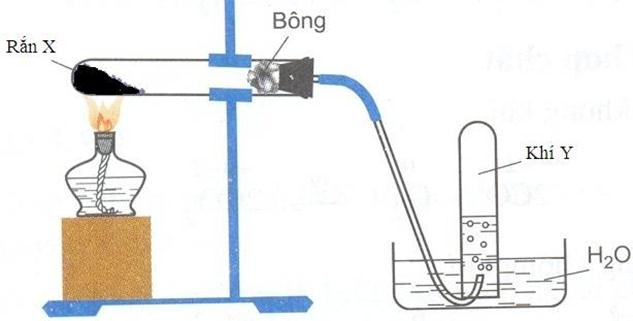
Dãy các khí đều có thể là khí Y trong thí nghiệm trên là
 Xem đáp án
Xem đáp án
Chọn D
Câu 136:
 Xem đáp án
Xem đáp án
Chọn B
Câu 137:
 Xem đáp án
Xem đáp án
Chọn D
Câu 138:
 Xem đáp án
Xem đáp án
Chọn A
Câu 139:
 Xem đáp án
Xem đáp án
Chọn D
Câu 140:
 Xem đáp án
Xem đáp án
Câu 141:
(1). Đổ thêm nước sôi ngập hạt mầm vào thời điểm bắt đầu thí nghiệm thì lượng kết tủa trong ống nghiệm càng nhiều.
(2). Có thể thay thế hạt nảy mầm bằng hạt khô và nước vôi trong bằng dung dịch NaOH loãng thì kết quả thí nghiệm không thay đổi.
(3). Do hoạt động hô hấp của hạt nên lượng CO2 tích luỹ trong bình ngày càng nhiều.
(4). Thí nghiệm chứng minh nước vừa là sản phẩm, vừa là nguyên liệu của hô hấp.
 Xem đáp án
Xem đáp án
Chọn C
Câu 143:
(1) tăng số lần nguyên phân, kích thích tăng trưởng chiều cao của cây
(2) kích thích nảy mầm của hạt
(3) kích thích phân chia tế bào và kích thích sinh trưởng chồi bên
(4) kích thích ra rễ phụ
(5) tạo quả không hạt
 Xem đáp án
Xem đáp án
Chọn D
Câu 144:
 Xem đáp án
Xem đáp án
Chọn A
Câu 145:
 Xem đáp án
Xem đáp án
Chọn C
Câu 146:
 Xem đáp án
Xem đáp án
Chọn D
Câu 147:
I. Tạo giống bống kháng sâu bệnh bằng cách chuyển gen trừ sâu từ vi khuẩn vào cây bông.
II.Tạo ra giống lúa “gạo vàng” có khả năng tổng hợp β - caroten.
III. Tạo giống dâu tằm tam bội có năng suất lá cao.
IV.Tạo cây pomato - cấy lai giữa khoai tây và cà chua.
Có bao nhiêu thành tựu được tạo ra nhờ công nghệ gen?
 Xem đáp án
Xem đáp án
Chọn D
Câu 148:
 Xem đáp án
Xem đáp án
Chọn C
Câu 149:
 Xem đáp án
Xem đáp án
Chọn C
Câu 150:
 Xem đáp án
Xem đáp án
