50 câu hỏi trắc nghiệm thuộc 25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết (Đề 5)

Câu 1:

Trong không gian Oxyz, cho đường thẳng d vuông góc với mặt phẳng $(P) : 4 x - z + 3 = 0$ . Véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng d?

A. $\vec{u} = (4; 1; - 1)$

B. $\vec{u} = (4; - 1; 3)$

C. $\vec{u} = (4; 0; - 1)$

D. $\vec{u} = (4; 1; 3)$

Xem đáp án

Do $d ⊥ (P)$ nên véctơ chỉ phương của đường thẳng $(d)$ là véctơ pháp tuyến của (P).

Suy ra một véctơ chỉ phương của đường thẳng $(d)$ là $\vec{u} = \vec{u_{(P)}} = (4; 0; - 1)$ .

Câu 2:

Cho hàm số

y = f (x)

liên tục tại

x_{0}

và có bảng biến thiên sau.

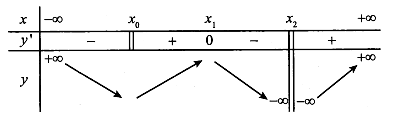
Đồ thị hàm số đã cho có

A. hai điểm cực trị, một điểm cực tiểu.

B. một điểm cực đại, không có điểm cực tiểu.

C. một điểm cực đại, hai điểm cực tiểu.

D. một điểm cực đại, một điểm cực tiểu

Xem đáp án

Tại $x = x_{2}$ hàm số $y = f (x)$ không xác định nên khôg đạt cực trị tại điểm này.

Tại $x = x_{1}$ thì dễ thấy hàm số đạt cực đại tại điểm này.

Tại $x = x_{0}$ , hàm số không có đạo hàm tại $x_{0}$ nhưng liên tục tại $x_{0}$ thì hàm số vẫn đạt cực trị tại $x_{0}$ và theo như bảng biến thiên thì đó là cực tiểu.

Vậy đồ thị hàm số có một điểm cực đại, một điểm cực tiểu.

Câu 3:

Tập nghiệm của bất phương trình $\log_{3} (x^{2} + 2) \leq 3$ là

A. $S = (- \infty; - 5] \cup [5; + \infty)$

B. $S = \emptyset$

C. $S = ℝ$

D. $S = [- 5; 5]$

Xem đáp án

Ta có:

\log_{3} (x^{2} + 2) \leq 3 \Leftrightarrow x^{2} + 2 \leq 27 \Leftrightarrow x^{2} \leq 25 \Leftrightarrow - 5 \leq x \leq 5

Câu 4:

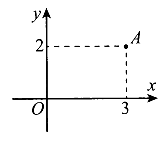
Điểm A trong hình vẽ bên biểu diễn cho số phức z. Tìm phần thực và phần ảo của số phức $\bar{z}$ .

Điểm A trong hình vẽ bên biểu diễn cho số phức z. Tìm phần thực và phần ảo của số phức z ngang. (ảnh 1)

A. Phần thực là -3 và phần ảo là 2.

B. Phần thực là 3 và phần ảo là -2.

C. Phần thực là 3 và phần ảo là -2i.

D. Phần thực là -3 và phần ảo là 2i.

Xem đáp án

Ta có: $z = 3 + 2 i \Rightarrow \bar{z} = 3 - 2 i$ .

Câu 5:

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ sau.

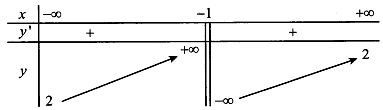
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau. Mệnh đề nào sau đây đúng? (ảnh 1)

Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên $ℝ \ \{- 1\}$

B. Hàm số đồng biến trên

(- \infty; - 1)

.

C. Hàm số đồng biến trên

(- \infty; 2)

.

D. Hàm số đồng biến trên R

Xem đáp án

Dựa vào bảng biến thiên hàm số đã cho đồng biến trên $(- \infty; - 1)$ và $(- 1; + \infty)$ .

Câu 6:

Cho ba điểm $A (1; - 3; 2), B (2; - 3; 1), C (- 3; 1; 2)$ và đường thẳng $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 3}{2}$ . Tìm điểm D có hoành độ dương trên d sao cho tứ diện ABCD có thể tích bằng 12.

A. $D (6; 5; 7)$

B. $D (1; - 1; 3)$

C. $D (7; 2; 9)$

D. $D (3; 1; 5)$

Xem đáp án

Ta có .

$D \in d \Leftrightarrow D (1 + 2 t; - 1 + t; 3 + 2 t), t \in ℝ$ .

. $\vec{A B} = (1; 0; - 1), \vec{A C} = (- 4; 4; 0) \Rightarrow [\vec{A B}, \vec{A C}] = (4; 4; 4)$

$\vec{A D} = (2 t; 2 + t; 1 + 2 t)$

$V_{A B C D} = \frac{1}{6} |[\vec{A B}, \vec{A C}] . \vec{A D}| \Leftrightarrow |4 (2 t) + 4 (2 + t) + 4 (1 + 2 t)| = 6.12 \Leftrightarrow |5 t + 3| = 18 \Leftrightarrow [\begin{array}{l} t = 3 \\ t = - \frac{21}{5} \end{array}$

Với t =3 suy ra D(7;2;9) (thỏa mãn điều kiện).

Với $t = - \frac{21}{5} \Rightarrow x_{D} = - \frac{37}{5} < 0$ (loại).

Câu 7:

Đặt $t = \sqrt{e^{x} + 4}$ thì $I = \int \frac{1}{\sqrt{e^{x} + 4}} d x$ trở thành

A. $I = \int \frac{2}{t (t^{2} - 4)} d t$

B. $I = \int \frac{t}{t (t^{2} - 4)} d t$

C. $I = \int \frac{2}{t^{2} - 4} d t$

D. $I = \int \frac{2 t}{t^{2} - 4} d t$

Xem đáp án

Đặt $t = \sqrt{e^{x} + 4} \Rightarrow t^{2} = e^{x} + 4 \Rightarrow 2 t d t = e^{x} d x \Rightarrow 2 t d t = (t^{2} - 4) d x \Rightarrow d x = \frac{2 t d t}{t^{2} - 4}$ .

Do đó $I = \int \frac{1}{\sqrt{e^{x} + 4}} d x = \int \frac{2}{t^{2} - 4} d t$ .

Câu 8:

Cho hàm số $y = f (x) = x^{3} + a x^{2} + b x + c (a, b, c \in ℝ)$ . Biết hàm số có hai điểm cực trị là x=1 ,x=2 và f(0)=1 . Giá trị của biểu thức $P = 2 a + b + c$ là

A. P = -2

B. P = 0

C. P = -1

D. P = 5

Xem đáp án

Ta có $f^{'} (x) = 3 x^{2} + 2 a x + b$ .

Theo giả thiết, ta có hệ phương trình

$\{\begin{cases} 3 + 2 a + b = 0 \\ 12 + 4 a + b = 0 \\ c = 1 \end{cases} \Rightarrow \{\begin{cases} a = - \frac{9}{2} \\ b = 6 \\ c = 1 \end{cases}$ .

Vậy $2 a + b + c = - 2$ .

Câu 9:

Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc $60 °$ . Thể tích V của khối chóp là

A. $V = \frac{a^{3} \sqrt{3}}{24}$

B. $V = \frac{a^{3} \sqrt{3}}{8}$

C. $V = \frac{a^{3} \sqrt{3}}{4}$

D. $V = \frac{a^{3} \sqrt{2}}{6}$

Xem đáp án

Gọi M là trung điểm AB, O là trọng tâm

$Δ A B C \Rightarrow C M ⊥ A B \Rightarrow \hat{((S A B), (A B C))} = \hat{S M O} = 60 °$ .

Mặt khác $M O = \frac{1}{3} . \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6} \Rightarrow S O = M O . \tan 60 ° = \frac{a \sqrt{3}}{6} . \sqrt{3} = \frac{a}{2}$ .

Suy ra $V_{S A B C} = \frac{1}{3} . \frac{a}{2} . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{24}$ .

Câu 10:

Cho hàm số y = f(x) có đạo hàm $f^{'} (x) = x {(x + 2)}^{2019} {(x^{2} - 1)}^{2020}$ . Số điểm cực trị của hàm số là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Ta có $f^{'} (x) = x {(x + 2)}^{2019} {(x^{2} - 1)}^{2020} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 2 \\ x = \pm 1 \end{array}$ .

Bảng xét dấu f(x):

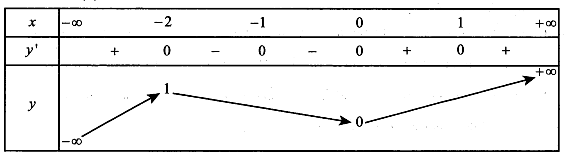
Cho hàm số y=f(x) có đạo hàm f'(x)=x(x+2)^2019(x^2-1)^2020 . (ảnh 1)

Vậy hàm số có hai điểm cực trị.

Câu 11:

Cho $\log 3 = m; \ln 3 = n$ . Hãy biểu diễn ln30 theo m và n.

A. $\ln 30 = \frac{n}{m} + 1$

B. $\ln 30 = \frac{m}{n} + n$

C. $\ln 30 = \frac{n + m}{n}$

D. $\ln 30 = \frac{n}{m} + n$

Xem đáp án

Ta có $\{\begin{cases} \log 3 = m \\ \ln 3 = n \end{cases} \Leftrightarrow \{\begin{cases} 3 = 10^{m} \\ 3 = e^{n} \end{cases} \Rightarrow 10^{n} = e^{n} \Leftrightarrow n = m \ln 10 \Leftrightarrow \ln 10 = \frac{n}{m}$ .

Vậy $\ln 30 = \ln 3 + \ln 10 = n + \frac{n}{m}$ .

Câu 12:

Với $x > a > 0$ và a là tham số, đặt $f (x) = \int_{0}^{x} \sqrt{t} \ln^{3} t d t$ . Hàm số f(x) đồng biến trên khoảng nào trong các khoảng sau đây?

A. (1;e)

B. $(\frac{1}{e}; + \infty)$

C. $(1; + \infty)$

D. $(e; + \infty)$

Xem đáp án

Giả sử F(t) là một nguyên hàm của $\sqrt{t} \ln^{3} t$ , ta có $F^{'} (t) = \sqrt{t} \ln^{3} t$ .

Khi đó

f (x) = F (x) - F (a) \Rightarrow f^{'} (x) = F^{'} (x) = \sqrt{x} \ln^{3} x > 0 \Leftrightarrow \ln x > 0 \Leftrightarrow x > 1

Câu 13:

Một hình nón có bán kính đáy bằng 1 và thiết diện qua trục là một tam giác vuông cân. Diện tích xung quanh của hình nón bằng

A. $\sqrt{2} π$

B. $π$

C. $2 \sqrt{2} π$

D. $\frac{1}{\sqrt{2}} π$

Xem đáp án

Ta có $l = R \sqrt{2} = \sqrt{2} \Rightarrow S_{x q} = π R l = π \sqrt{2}$ .

Câu 14:

Trong không gian Oxyz, phương trình mặt cầu đi qua bốn điểm O, $A (1; 0; 0), B (0; - 2; 0)$ và $C (0; 0; 4)$ là

A. $(S) : x^{2} + y^{2} + z^{2} + x - 2 y + 4 z = 0$

B. $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 8 z = 0$

C. $(S) : x^{2} + y^{2} + z^{2} - x + 2 y - 4 z = 0$

D. $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y + 8 z = 0$

Xem đáp án

Giả sử phương trình mặt cầu có dạng

$(S) : x^{2} + y^{2} + z^{2} - 2 a x - 2 b y - 2 c x + d = 0 (a^{2} + b^{2} + c^{2} - d > 0)$

Vì mặt cầu (S) đi qua O, $A (1; 0; 0), B (0; - 2; 0)$ và C(0;0;4) nên ta có hệ phương trình

\{\begin{cases} d = 0 \\ 1^{2} + 0 + 0 - 2.1. a + d = 0 \\ 0 + {(- 2)}^{2} + 0 - 2 (- 2) . b + d = 0 \\ 0 + 0 + 4^{2} - 2.4. c + d = 0 \end{cases} \Leftrightarrow \{\begin{cases} d = 0 \\ a = \frac{1}{2} \\ b = - 1 \\ c = 2 \end{cases} \Rightarrow (S) : x^{2} + y^{2} + z^{2} - x + 2 y - 4 z = 0

.

Câu 15:

Cho hàm số f(x) có bảng biến thiên như sau.

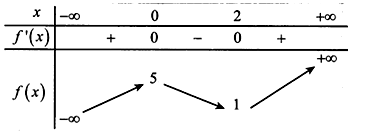
Cho hàm số f(x) có bảng biến thiên như sau. Khẳng định nào sau đây là đúng? (ảnh 1)

Khẳng định nào sau đây là đúng?

A. Giá trị cực đại của hàm số bằng 1.

B. Giá trị cực đại của hàm số bằng 5.

C. Giá trị cực tiểu của hàm số bằng 2.

D. Giá trị cực đại của hàm số bằng 0

Xem đáp án

Dựa vào bảng biến thiên ta thấy giá trị cực đại của hàm số bằng 5.

Câu 16:

Buổi sáng ông Tần vừa nhập một lượng dưa hấu từ nông dân và bán cho khách. Ông thống kê lại số dưa bán được theo giờ. Giờ thứ nhất bán được nửa số dưa và nửa quả, giờ thứ hai bán được nửa số dưa còn lại và nửa quả, giờ thứ 3 bán được nửa số dưa còn lại và nửa quả… Đến giờ thứ 5 sau khi bán được nửa số dưa còn lại và nửa quả thì ông còn dư 1 quả. Hỏi buổi sáng ông Tần đã nhập vào bao nhiêu quả dưa hấu?

A. 127 quả

B. 63 quả

C. 45 quả

D. 105 quả

Xem đáp án

Gọi x là số quả dưa ông Tần đã nhập. Ta có:

Giờ thứ nhất bán được $\frac{x}{2} + \frac{1}{2} = \frac{x + 1}{2}$ (quả).

Giờ thứ 2 bán được $\frac{1}{2} (x - \frac{x + 1}{2}) + \frac{1}{2} = \frac{x + 1}{2^{2}}$ (quả)

….

Giờ thứ 5 bán được $\frac{x + 1}{2^{5}}$ (quả).

Vậy $(x + 1) (\frac{1}{2} + \frac{1}{2^{2}} + ... \frac{1}{2^{5}}) = x - 1$ .

Tổng cấp số nhân

\frac{1}{2} + \frac{1}{2^{2}} + ... \frac{1}{2^{5}} = \frac{1}{2} . \frac{1 - \frac{1}{2^{5}}}{\frac{1}{2}} = \frac{31}{32} \Leftrightarrow (x + 1) \frac{31}{32} = x - 1 \Leftrightarrow x = 63

Câu 17:

Cho hình chóp S.ABCD có đáy là hình vuông. Trên AB lấy một điểm M. Gọi $(α)$ là mặt phẳng qua M và song song với mặt phẳng $(S A D)$ cắt SB, SC và CD lần lượt tại N, P, Q. Thiết diện của $(α)$ với hình chóp là

A. hình thoi MNPQ.

B. hình thang MNPQ.

C. hình thang cân MNPQ.

D. hình bình hà

Xem đáp án

Ta có: $(α) // (S A D) \Leftrightarrow \{\begin{cases} (α) // SD \\ (α) // SA \\ (α) // AD \end{cases}$ .

+ Với $(α) // SD$ , ta có $\{\begin{cases} (α) // SD \\ S D \subset (S A D) \\ (α) \cap (S A D) = P Q \\ (α) // SA \end{cases} \Rightarrow P Q // SD$ .

+ Với $(α) // SA$ , ta có $\{\begin{cases} (α) // SA \\ SA \subset (S A B) \\ (α) \cap (S A B) = M N \end{cases} \Rightarrow M N // SA$ .

+ Với $(α) // AD$ , ta có $\{\begin{cases} (α) // AD \\ A D \subset (A B C D) \\ (α) \cap (A B C D) = M Q \end{cases} \Rightarrow M Q // AD$ (1).

Lại có $\{\begin{cases} B C // MQ \\ BC ⊄ (α) \end{cases} \Rightarrow (α) // BC$ , $\{\begin{cases} (α) // BC \\ BC \subset (S B C) \\ (α) \cap (S B C) = P N \end{cases} \Rightarrow P N // BC$ (2).

Từ (1) và (2), suy ra

M Q // PN \Rightarrow M N P Q

là hình thang

Câu 18:

Kí hiệu $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2} - 2 z + 5 = 0$ . Giá trị của $|z_{1}| + |z_{2}|$ bằng

A. $2 \sqrt{5}$

B. $\sqrt{5}$

C. 3

D. 10

Xem đáp án

Ta có: $z^{2} - 2 z + 5 = 0 \Leftrightarrow [\begin{array}{l} z_{1} = 1 + 2 i \\ z_{2} = 1 - 2 i \end{array}$ .

Suy ra $|z_{1}| = |z_{2}| = \sqrt{5} \Rightarrow |z_{1}| + |z_{2}| = 2 \sqrt{5}$ .

Câu 19:

Trong các hàm số sau hàm số nào là đạo hàm của hàm số $y = 2^{x} {.5}^{x}$ ?

A. $10^{x} \ln 10$

B. $10^{x}$

C. $2^{x} + 5^{x}$

D. $x {.10}^{x - 1}$

Xem đáp án

Ta có $y^{'} = {(2^{x})}^{'} {.5}^{x} + 2^{x} . {(5^{x})}^{'} = 2^{x} {.5}^{x} \ln 2 + 2^{x} {.5}^{x} \ln 5 = 10^{x} (\ln 2 + \ln 5) = 10^{x} . \ln 10$ .

Câu 20:

Cho hàm số 7-f(x) có đồ thì hàm số y=f'(x) như hình vẽ. Biết f(a) >0 . Hỏi đồ thị hàm số

y = |f (x) + 2020 m|

có tối đa bao nhiêu điểm cực trị?

A. 3

B. 4

C. 5

D. 7

Xem đáp án

Từ đồ thị của hàm số y= f'(x) ta có bảng biến thiên:

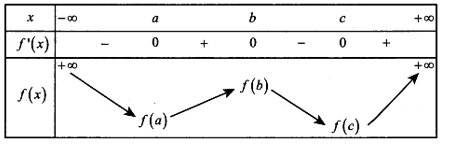
Cho hàm số y= f(x) có đồ thì hàm số y=f'(x) như hình vẽ. Biết f(a)>0 . (ảnh 1)

Hàm số y= f(x) có 3 điểm cực trị.

Để đồ thị hàm số $y = |f (x) + 2020 m|$ có số điểm cực trị lớn nhất thì y = f(x) cắt trục hoành tại số điểm là nhiều nhất => f(c)<0.

Từ bảng biến thiên ta thấy đồ thị hàm số y=f(x) cắt Ox tại nhiều nhất 2 điểm nên hàm số $y = |f (x) + 2020 m|$ có tối đa 5 điểm cực trị.

Câu 21:

Một cốc nước hình trụ có chiều cao là $h = 3 π$ (cm) bên trong đựng một lượng nước. Biết rằng khi nghiêng chiếc cốc sao cho lượng nước chạm mép cốc thì đồng thời nước cũng vừa chạm vào bán kính đáy cốc. Hỏi khi nghiêng cốc sao cho lượng nước vừa đủ phủ kín đáy cốc thì điểm còn lại mà lượng nước chạm vào thành cốc cách đáy cốc một khoảng bằng bao nhiêu?

A. $2 π c m$

B. $π c m$

C. 4 cm

D. 3cm

Xem đáp án

Thể tích hình nêm: $V = \frac{2}{3} R^{3} \tan α$ Thể tích hình trụ cụt: $V = π R^{2} (\frac{h_{1} + h_{2}}{2})$

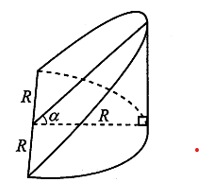
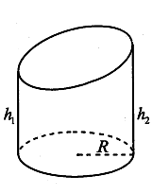
Thể tích của lượng nước không đổi nên $V = \frac{2}{3} R^{3} \tan α = π R^{2} (\frac{h_{1} + h_{2}}{2})$ trong đó $\tan α = \frac{h}{R}; h_{1} = 0$ .

Khi đó $V = \frac{2}{3} R^{3} \frac{h}{R} = π R^{2} (\frac{h_{2}}{2}) \Leftrightarrow \frac{2}{3} R^{2} h = π R^{2} (\frac{h_{2}}{2}) \Leftrightarrow h_{2} = \frac{4 h}{3 π} = 4$ (cm).

Câu 22:

Cho hình trụ có hai đáy là hai đường tròn (O) và (O'), chiều cao bằng 2R và bán kính đáy R. Một mặt phẳng

(α)

đi qua trung điểm của OO' và tạo với một góc

30 °

,

(α)

cắt đường tròn đáy theo một dây cung có độ dài bằng

A. $\frac{4 \sqrt{3} R}{9}$

B. $\frac{2 R \sqrt{6}}{3}$

C. $\frac{2 \sqrt{3} R}{3}$

D. $\frac{2 R}{3}$

Xem đáp án

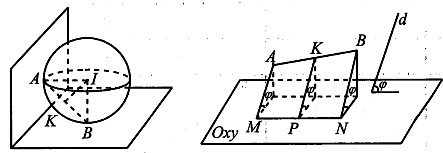
Dựng $O H ⊥ A B \Rightarrow A B ⊥ (O I H) \Rightarrow (O I H) ⊥ (I A B)$

=> đường thẳng IH là hình chiếu của đường thẳng OI lên $(I A B)$ .

Ta có $\hat{O I H} = 30 °$ .

Xét tam giác vuông OIH vuông tại $O \Rightarrow O H = O I \tan 30 ° = \frac{R \sqrt{3}}{3}$ .

Xét tam giác OHA vuông tại H

$\Rightarrow A H = \sqrt{O A^{2} - O H^{2}} = \frac{R \sqrt{6}}{3} \Rightarrow A B = \frac{2 R \sqrt{6}}{3}$ .

Câu 23:

Tập nghiệm S của phương trình $2^{2 x + 1} - {5.2}^{x} + 2 = 0$ là

A. $S = \{- 1; 1\}$

B. $S = \{- 1; 0\}$

C. $S = \{1\}$

D. $S = \{0; 1\}$

Xem đáp án

Phương trình:

2^{2 x + 1} - {5.2}^{x} + 2 = 0 \Leftrightarrow 2 {(2^{x})}^{2} - {5.2}^{x} + 2 = 0 \Leftrightarrow [\begin{array}{l} 2^{x} = 2 \\ 2^{x} = \frac{1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 1 \end{array}

.

Câu 24:

Cho x, y ( $x \neq 1$ ) là hai số thực dương thỏa mãn $\log_{\sqrt{x}} y = \frac{2 y}{5}, \log_{\sqrt[3]{5}} x = \frac{15}{y}$ . Giá trị của biểu thức $P = y^{2} + x^{2}$ là

A. P = 17

B. P = 50

C. P = 51

D. P = 40

Xem đáp án

Ta có $\log_{\sqrt{x}} y = \frac{2 y}{5} \Leftrightarrow \log_{x} y = \frac{y}{5}$ (1).

Lại có $\log_{\sqrt[3]{5}} x = \frac{15}{y} \Leftrightarrow \log_{5} x = \frac{5}{y}$ (2).

Từ (1) và (2), ta có . $\log_{x} y = \frac{1}{\log_{5} x} \Leftrightarrow \log_{x} y = \log_{x} 5 \Leftrightarrow y = 5$

Thay vào (2), suy ra

x = 5

. Vậy

P = y^{2} + x^{2} = 50

.

Câu 25:

Cho số phức z thỏa mãn |z|=2 . Tập hợp điểm biểu diễn số phức $w = (1 - i) \bar{z} + 2 i$ là

A. một đường tròn.

B. một đường thẳng.

C. một Elip.

D. một parabol hoặc hyperbol.

Xem đáp án

Ta có . $w = (1 - i) \bar{z} + 2 i \Leftrightarrow w - 2 i = (1 - i) \bar{z} \Rightarrow |w - 2 i| = |(1 - i)| |\bar{z}| \Leftrightarrow |w - 2 i| = 2 \sqrt{2}$

Do đó tập hợp điểm biểu diễn số phức w là đường tròn tâm I(0;2) và bán kính $2 \sqrt{2}$ .

Câu 26:

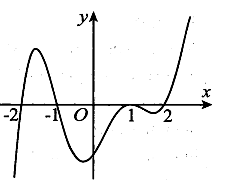
Cho hàm số y=f(x) là hàm đa thức bậc 5 có đồ thị hàm số y=f'(x) như hình vẽ. Hàm số y=f(x) đồng biến trên những khoảng nào trong các khoảng sau đây?

Cho hàm số y =f(x) là hàm đa thức bậc 5 có đồ thị hàm số y=f'(x) (ảnh 1)

A. $(- \infty; - 1)$ và $(1; + \infty)$

B.(

- \infty; - 2

) và (-1;2)

C. $(- \infty; - 2)$ và $(+ \infty; 2)$

D. $(- 2; - 1)$ và $(+ \infty; 2)$

Xem đáp án

Ta có f'(x) chỉ chọn các nghiệm x=-2;x=-1;x=2 và lập trục xét dấu

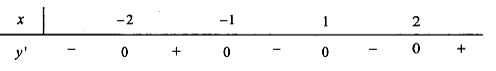
Cho hàm số y =f(x) là hàm đa thức bậc 5 có đồ thị hàm số y=f'(x) (ảnh 2)

Từ bảng biến thiên suy ra hàm số y=f(x) đồng biến trên các khoảng (-2;-1) và

(2; + \infty)

Câu 27:

Cho $f^{'} (x) = \frac{2}{{(2 x - 1)}^{2}} - \frac{1}{{(x - 1)}^{2}}$ thỏa mãn $f (2) = - \frac{1}{3}$ . Biết phương trình $f (x) = - 1$ có nghiệm duy nhất $x = x_{0}$ . Giá trị của biểu thức $T = 2020^{x_{0}}$ là

A. T = 2020

T= 1

D. $T = \sqrt{2020}$

D. $T = 2020^{3}$

Xem đáp án

Ta có $f (x) = \int f^{'} (x) = - \frac{1}{2 x - 1} + \frac{1}{x - 1} + C$ .

Mặt khác $f (2) = - \frac{1}{3} \Rightarrow C = - 1$ .

Xét phương trình $- \frac{1}{2 x - 1} + \frac{1}{x - 1} = 0 \Rightarrow x = 0$ .

Vậy $x = x_{0} = 0 \Rightarrow T = 1$ .

Câu 28:

Trong một lớp học có 35 học sinh. Muốn chọn ra một lớp trưởng, một lớp phó thì số cách chọn là

A. $C_{35}^{2}$

B. $A_{35}^{2}$

C. $2! 35$

D. $2 C_{35}^{1}$

Xem đáp án

Chọn ra một lớp trưởng, một lớp phó từ 35 học sinh (tức là một chỉnh hợp chập 2 của 35 phần tử) hay $A_{35}^{2}$ .

Câu 29:

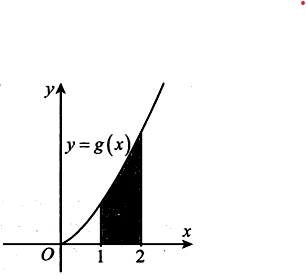
Cho hàm số $y = f (x)$ có đạo hàm liên tục trên R và hàm số $y = g (x) = x f (x^{2})$ có đồ thị trên đoạn $[0; 2]$ như hình vẽ. Biết diện tích miền màu xám là $S = \frac{5}{2}$ , giá trị tích phân $I = \int_{1}^{4} f (x) d x$ là

Cho hàm số y = f(x) có đạo hàm liên tục trên R và hàm số y=g()=xf(x^2) có đồ thị trên đoạn (ảnh 1)

A. $I = \frac{5}{4}$

B. $I = \frac{5}{2}$

C. I = 5

D. I =10

Xem đáp án

Đặt $x^{2} = t$ , ta có $S = \int_{1}^{2} x f (x^{2}) d x = \int_{1}^{4} \frac{1}{2} f (t) d t$

$\Leftrightarrow S = \int_{1}^{4} \frac{1}{2} f (t) d t = \frac{1}{2} \int_{1}^{4} f (x) d x = \frac{1}{2} I \Rightarrow I = 2 S = 5$ .

Câu 30:

Trong không gian với hệ tọa độ Oxyz, gọi $(α)$ là mặt phẳng chứa đường thẳng $(d) : \frac{x - 2}{1} = \frac{y - 3}{1} = \frac{z}{2}$ và vuông góc với mặt phẳng $(β) : x + y - 2 z + 1 = 0$ . Giao tuyến của $(α)$ và $(β)$ đi qua điểm nào dưới đây?

A. (0;1;3)

B. (2;3;3)

C. (5;6;8)

D. (1;-2;0)

Xem đáp án

Ta có $\vec{u_{d}} (1; 1; 2)$ là một véctơ chỉ phương của đường thẳng d.

$\vec{n_{P}} (1; 1; - 2)$ là một véctơ chỉ phương của $(β) \Rightarrow \vec{n_{α}} = [\vec{u_{d}}; \vec{n_{P}}] = (- 4; 4; 0)$ .

$A (2; 3; 0) \in d \Rightarrow A \in (α)$ .

Phương trình mặt phẳng $(α) : - 4 (x - 2) + 4 (y - 3) + 0 (z - 0) = 0 \Leftrightarrow - 4 x + 4 y - 4 = 0 \Leftrightarrow x - y + 1 = 0$ .

Giả sử $M (x; y; z) \in (α) \cap (β)$ . Khi đó tọa độ M thỏa mãn hệ $\{\begin{cases} x - y + 1 = 0 \\ x + y - 2 z + 1 = 0 \end{cases}$ .

Thay các đáp án vào hệ trên ta thấy M(2;3;3) thỏa mãn.

Câu 31:

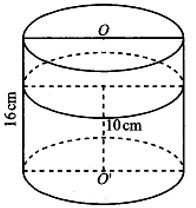
Một chiếc cốc có dạng hình trụ, chiều cao là 16cm, đường kính đáy bằng 8cm, bề dày thành cốc và đáy cốc là 1cm. Nếu đổ một lượng nước vào cốc cách miệng cốc 5cm thì ta được khối nước có thể tích $V_{1}$ , nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích $V_{2}$ . Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

A. $\frac{2}{3}$

B. $\frac{11}{6}$

C. $\frac{245}{512}$

D. $\frac{45}{128}$

Xem đáp án

Gọi $r_{1}, r_{2}$ lần lượt là bán kính trong và bán kính ngoài (tính cả bề dày thành cốc) khi đó ta có $r_{1} = 3, r_{2} = 4$ .

Gọi $h_{1}, h_{2}$ lần lượt là chiều cao cột nước trong cốc và chiều cao hình trụ, khi đó ta có $r_{1} = 3, r_{2} = 4$ .

Thể tích lượng nước $h_{1} = 10, h_{2} = 16$ .

Thể tích khối trụ $V_{1} = π r_{1}^{2} h_{1} = π {.3}^{2} .10 = 90 π$ .

Vậy $\frac{V_{1}}{V_{2}} = \frac{90 π}{256 π} = \frac{45}{128}$

Một chiếc cốc có dạng hình trụ, chiều cao là 16cm, đường kính đáy bằng 8cm, (ảnh 1)

Câu 32:

Cho hàm số y= f(x) đồng biến trên $(0; + \infty)$ ; y =f(x) liên tục, nhận giá trị dương trên $(0; + \infty)$ và thỏa mãn $f (3) = \frac{2}{3}$ và ${[f^{'} (x)]}^{2} = (x + 1) . f (x)$ . Mệnh đề nào dưới đây đúng?

A. $2613 < f^{2} (8) < 2614$

B. $2614 < f^{2} (8) < 2615$

C. $2618 < f^{2} (8) < 2619$

D. $2616 < f^{2} (8) < 2617$

Xem đáp án

Hàm số $y = f (x)$ đồng biến trên $(0; + \infty)$ nên $f^{'} (x) \geq 0, \forall x \in (0; + \infty)$ .

Mặt khác y =f(x) liên tục, nhận giá trị dương trên $(0; + \infty)$ nên ${[f^{'} (x)]}^{2} = (x + 1) . f (x) \Rightarrow f^{'} (x) = \sqrt{(x + 1) . f (x)}, \forall x \in (0; + \infty)$

$\Rightarrow \frac{f^{'} (x)}{\sqrt{f (x)}} = \sqrt{(x + 1)}, \forall x \in (0; + \infty)$

$\Rightarrow \int \frac{f^{'} (x)}{f (x)} d x = \int \sqrt{x + 1} d x \Rightarrow \sqrt{f (x)} = \frac{1}{3} \sqrt{{(x + 1)}^{3}} + C$

.

Từ $f (3) = \frac{2}{3}$ suy ra $C = \sqrt{\frac{2}{3}} - \frac{8}{3}$ .

Như vậy $f (x) = {(\frac{1}{3} \sqrt{{(x + 1)}^{3}} + \sqrt{\frac{2}{3}} - \frac{8}{3})}^{2}$ .

Do đó

f (8) = {(\frac{1}{3} \sqrt{{(8 + 1)}^{3}} + \sqrt{\frac{2}{3}} - \frac{8}{3})}^{2} = {(9 + \sqrt{\frac{2}{3}} - \frac{8}{3})}^{2} \Rightarrow f^{2} (8) = {(9 + \sqrt{\frac{2}{3}} - \frac{8}{3})}^{4} \approx 2613, 26

.

Câu 33:

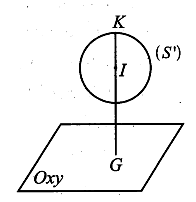
Cho tam giác ABC đều cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với (ABC) . Trong (P) xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C) và đỉnh A bằng

A. $\frac{π a^{2}}{2}$

B. $\frac{π a^{2}}{3}$

C. $π . a^{2}$

D. $2 πa$

Xem đáp án

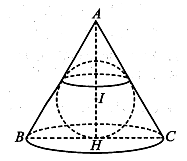
Cho tam giác ABC đều cạnh a. Gọi (P) là mặt phẳng chứa BC (ảnh 1)

Mặt cầu nội tiếp hình nón để cho có 1 đường tròn lớn nội tiếp tam giác đều ABC (cạnh a).

Do đó mặt cầu đó có bán kính $r = \frac{1}{3} . \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6}$ .

Vậy diện tích mặt cầu cần tìm là $V = 4 π r^{2} = 4 π {(\frac{a \sqrt{3}}{6})}^{2} = \frac{π a^{2}}{3}$ .

Câu 34:

Cho hàm số . Hàm số y =f(x) có đồ thị như hình vẽ. Hàm số y=f(2-e^x) đồng biến trên khoảng (ảnh 1)

Cho hàm số y = f(x) . Hàm số

y = f (2 - e^{x})

có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng

A. $(0; \ln 3)$

B. $(1; + \infty)$

C. (-1;1)

D. $(- \infty; 0)$

Xem đáp án

Ta có . $y^{'} = - e^{x} f^{'} (2 - e^{x})$

. $y^{'} = 0 \Leftrightarrow [\begin{array}{l} 2 - e^{x} = - 1 \\ 2 - e^{x} = 1 \\ 2 - e^{x} = 4 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \ln 3 \end{array}$

Bảng biến thiên

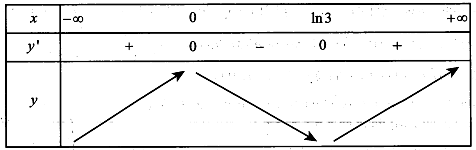
Cho hàm số . Hàm số y =f(x) có đồ thị như hình vẽ. Hàm số y=f(2-e^x) đồng biến trên khoảng (ảnh 2)

Dựa vào bảng biến thiên suy ra hàm số $y = f (2 - e^{x})$ đồng biến trên các khoảng $(\ln 3; + \infty)$ và $(- \infty; 0)$ .

Câu 35:

Tại sân ga, có một đoàn tàu gồm 8 toa. Có 5 hành khách lên tàu, độc lập với nhau, mỗi người lên 1 toa ngẫu nhiên. Xác suất để sau khi hành khách lên tàu, đoàn tàu còn 7 toa trống là

A. $\frac{1}{8^{5}}$

B. $\frac{2}{8^{4}}$

C. $\frac{1}{2 . 8^{4}}$

D. $\frac{1}{8^{4}}$

Xem đáp án

Ta có $n (Ω) = 8^{5}$ .

Gọi A là biến cố: “Sau khi hành khách lên tàu xong, đoàn tàu có 7 toa trống”.

Vậy có đúng 1 toa tàu có khách. Khi đó tính số kết quả thuận lợi theo trình tự sau:

+ Chọn 1 toa tàu để các hành khách đi lên đó, có $C_{8}^{1}$ cách.

+ Xếp 5 hành khách cùng vào toa tàu vừa chọn ta có được $1^{5} = 1$ cách chọn.

Vậy số kết quả thuận lợi cho biến cố A là $n (A) = C_{8}^{1} .1 = 8$ .

Vậy xác suất của biến cố A là $P (A) = \frac{n (A)}{n (Ω)} = \frac{8}{8^{5}} = \frac{1}{8^{4}}$ .

Câu 36:

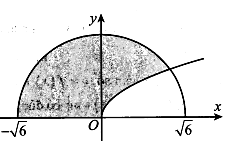
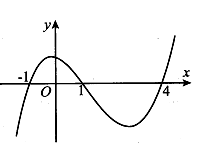
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = căn x, cung tròn có phương trình (ảnh 1)

Gọi D là hình phẳng giới hạn bởi đồ thị hàm số $y = \sqrt{x}$ , cung tròn có phương trình $y = \sqrt{6 - x^{2}} (- \sqrt{6} \leq x \leq \sqrt{6})$ và tục hoành (phần tô đậm trong hình vẽ bên). Thể tích V của vật thể tròn xoay sinh ra khi quay hình phẳng D quanh trục Ox là

A. $V = 8 π \sqrt{6} - 2 π$

B. $V = 8 π \sqrt{6} + \frac{22 π}{3}$

C. $V = 8 π \sqrt{6} - \frac{22 π}{3}$

D. $V = 4 π \sqrt{6} + \frac{22 π}{3}$

Xem đáp án

Cung tròn khi quay quanh Ox tạo thành một khối cầu có thể tích $V_{1} = \frac{4}{3} π {(\sqrt{6})}^{3} = 8 π \sqrt{6}$ .

Xét phương trình $\sqrt{x} = \sqrt{6 - x^{2}} \Leftrightarrow \{\begin{cases} x > 0 \\ x^{2} + x - 6 = 0 \end{cases} \Leftrightarrow x = 2$ .

Thể tích khối tròn xoay có được khi quay hình phẳng (H) giới hạn bởi đồ thị các hàm số $y = \sqrt{x}$ , cung tròn có phương trình $y = \sqrt{6 - x^{2}}$ và đường thẳng y =0 quanh Ox là: $V_{2} = π \int_{0}^{2} x dx + π \int_{2}^{\sqrt{6}} (6 - x^{2}) d x = 2 π + \frac{12 \sqrt{6} - 28}{3} π = 4 π \sqrt{6} - \frac{22 π}{3}$

.Vậy thể tích vật thể tròn xoay cần tìm là $V = V_{1} - V_{2} = 8 π \sqrt{6} - (4 π \sqrt{6} - \frac{22 π}{3}) = 4 \sqrt{6} π + \frac{22 π}{3}$

Câu 37:

Cho hàm số

y = f (x)

có đồ thị như hình vẽ bên. Đặt

g (x) = 2 f (x) - x^{2}

. Biết rằng

g (0) + g (- 1) = g (1) + g (2)

. Khẳng định nào dưới đây là đúng?

A. $g (0) > g (1) > g (2) > g (- 1)$

B. $g (0) > g (- 1) > g (1) > g (2)$

C. $g (0) > g (1) > g (- 1) > g (2)$

D. $g (0) > g (1) = g (- 1) > g (2)$

Xem đáp án

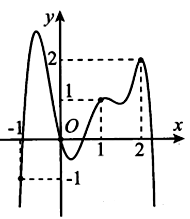
Ta có $g^{'} (x) = 2 f^{'} (x) - 2 x$ , vẽ thêm đường thẳng $y = x$ .

Ta có $g^{'} (x) = 0 \Leftrightarrow f^{'} (x) = x \Leftrightarrow [\begin{array}{l} x = \pm 1 \\ x = 0 \\ x = 2 \end{array}$ .

Lập bảng biến thiên

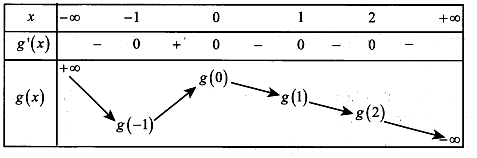
Cho hàm số y =f(x) có đồ thị y=f'(x) như hình vẽ bên. Đặt . Biết rằng (ảnh 2)

Từ bảng biến thiên ta dễ thấy $\max_{[- 1; 2]} g (x) = g (0)$ và $g (1) > g (2)$ .

Do $g (0) > g (1) \Rightarrow g (0) + g (- 1) = g (1) + g (2) < g (0) + g (2) \Leftrightarrow g (- 1) < g (2)$ .

Vậy $g (0) > g (1) > g (2) > g (- 1)$ .

Câu 38:

Xét các số phức z, w thỏa mãn $|w - i| = 2, z + 2 = i w$ . Gọi $z_{1}, z_{2}$ lần lượt là các số phức mà tại đó đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Môđun $|z_{1} + z_{2}|$ bằng

A. $3 \sqrt{2}$

B. 3

C. 6

D. $6 \sqrt{2}$

Xem đáp án

Xét các số phức z, w thỏa mãn |w-i|=2,z+2=iw . (ảnh 2)

Xét các số phức z, w thỏa mãn |w-i|=2,z+2=iw . (ảnh 1)

Câu 39:

Cho lăng trụ đều tam giác ABCA'B'C' có cạnh AB=2a, M là trung điểm của A'B' ,

d (C^{'}, (M B C)) = \frac{a \sqrt{2}}{2}

. Thể tích khối lăng trụ ABC.A'B'C' bằng

A. $\frac{\sqrt{2}}{3} a^{3}$

B. $\frac{\sqrt{2}}{6} a^{3}$

C. $\frac{3 \sqrt{2}}{2} a^{3}$

D. $\frac{\sqrt{2}}{2} a^{3}$

Xem đáp án

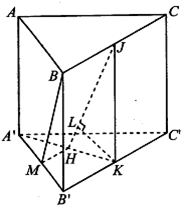
Cho lăng trụ đều tam giác có cạnh Cho lăng trụ đều tam giác ABCA'B'C' có cạnh AB=2a , M là trung điểm của (ảnh 1)

Gọi J, K, H theo thứ tự là trung điểm của BC, $B^{'} C^{'}, K$ .

$M H // BC \Rightarrow (M B C) \equiv (M H J B)$ .

$B^{'} C^{'} // (M B C) \Rightarrow d (C^{'}, (M B C)) = d (K, (M B C))$ .

$M H ⊥ K, M H ⊥ J K \Rightarrow M H ⊥ (J K H) \Rightarrow (J K H) ⊥ (M H J B)$ .

Gọi L là hình chiếu của K trên $J H \Rightarrow d (K, (M B C)) = K L$ .

Tam giác JKH vuông tại K có đường cao $K L = \frac{a \sqrt{2}}{2}, K H = \frac{a \sqrt{3}}{2}$ ;

$\frac{1}{K L^{2}} = \frac{1}{K H^{2}} + \frac{1}{K J^{2}} \Rightarrow K J = \frac{a \sqrt{6}}{2}$ là độ dài dường cao của lăng trụ.

Vậy $V_{A B C . A^{'} B^{'} C^{'}} = K J . S_{A B C} = \frac{3 \sqrt{2}}{2} a^{3}$ .

Câu 40:

Có bao nhiêu giá trị nguyên $m \in [0; 2021]$ để phương trình ${(2 + \sqrt{3})}^{x} + {(2 - \sqrt{3})}^{x} = m$ có hai nghiệm phân biệt?

A. 2016

B. 2017

C. 2018

D.2019

Xem đáp án

Đặt $t = {(2 + \sqrt{3})}^{x}; t > 0$ .

Phương trình đã cho trở thành $t + \frac{1}{t} = m$ (*)

Xét hàm số $f (t) = t + \frac{1}{t}$ xác định và liên tục trên $(0; + \infty)$ .

Ta có $f^{'} (t) = 1 - \frac{1}{t^{2}}$ . Cho $f^{'} (t) = 0 \Leftrightarrow t = \pm 1$ .

Bảng biến thiên

Có bao nhiêu giá trị nguyên m thuộc [0;2021] để phương trình (ảnh 1)

Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm dương phân biệt <=> m>2.

Vậy $m \in \{3; 4; 5; ...; 2021\}$ nên có 2019 giá trị thỏa mãn.

Câu 41:

Trong không gian Oxyz, cho điểm A(10;2;1) và đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 1}{3}$ . Gọi (P) là mặt phẳng đi qua điểm A, song song với đường thẳng d sao cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm $M (- 1; 2; 3)$ đến mặt phẳng (P) là

A. $\frac{97 \sqrt{3}}{15}$

B. $\frac{76 \sqrt{790}}{790}$

C. $\frac{2 \sqrt{13}}{13}$

D. $\frac{3 \sqrt{29}}{29}$

Xem đáp án

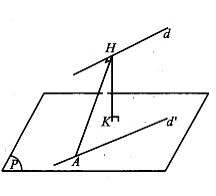
(P) là mặt phẳng đi qua điểm A và song song với đường thẳng d nên (P) chứa đướng thẳng d' đi qua điểm A và song song với đường thẳng d.

Gọi H là hình chiếu của A trên d, K là hình chiếu của H trên (P).

Ta có $d (d, (P)) = H K \leq A H$ (AH không đổi)

Giá trị lớn nhất của $d (d, (P))$ là AH

$d (d, (P))$ lớn nhất khi AH vuông góc với (P).

Khi đó nếu gọi (Q) là mặt phẳng chứa A và d thì (P) vuông góc với (Q)

$\Rightarrow \vec{n_{P}} = [\vec{u_{d}}, \vec{n_{Q}}] = (98; 14; - 70)$

$\Rightarrow (P) : 7 x + y - 5 z - 77 = 0 \Rightarrow d (M, (P)) = \frac{97 \sqrt{3}}{15}$

Trong không gian Oxyz, cho điểm A(10;2;1) và đường thẳng d:x-1/2=y/1=z-1/3 . (ảnh 1)

Câu 42:

Cho tứ diện ABCD có AB=CD=a;AC=BD=b;AD=BC=c . Giá trị côsin góc giữa hai đường thẳng AC và BD bằng

A. $|\frac{3 (b^{2} - a^{2})}{c^{2}}|$

B. $|\frac{2 (b^{2} - a^{2})}{c^{2}}|$

C. $|\frac{a^{2} - c^{2}}{b^{2}}|$

D. $|\frac{3 (a^{2} - c^{2})}{b^{2}}|$

Xem đáp án

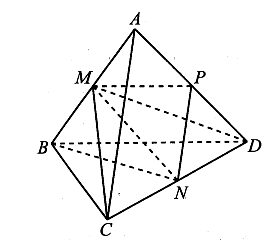
Cho tứ diện ABCD có AB=CD=a;AC=BD=b;AD=BC=c . Giá trị côsin góc giữa hai đường thẳng AC và BD bằng (ảnh 1)

Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CD, AD.

Ta có $\{\begin{cases} P M // BD \\ P N / / A C \end{cases} \Rightarrow \hat{(B D, A C)} = \hat{(P M, P N)}$ .

Theo công thức tính đường trung tuyến ta có

$C M^{2} = \frac{C A^{2} + C B^{2}}{2} - \frac{A B^{2}}{4} = \frac{2 (b^{2} + c^{2}) - a^{2}}{4}$ .

Tương tự $D M^{2} = \frac{2 (b^{2} + c^{2}) - a^{2}}{4}$ nên:

$M N^{2} = \frac{M C^{2} + M D^{2}}{2} - \frac{C D^{2}}{4} = \frac{2 (b^{2} + c^{2})}{4} - \frac{a^{2}}{4} = \frac{b^{2} + c^{2} - a^{2}}{2}$

Áp dụng định lí Cô-sin cho tam giác PMN ta có:

$\cos \hat{M P N} = \frac{P M^{2} + P N^{2} - M N^{2}}{2 P M . P N} = \frac{{(\frac{b}{2})}^{2} + {(\frac{b}{2})}^{2} - \frac{b^{2} + c^{2} - a^{2}}{2}}{2 (\frac{b}{2}) (\frac{b}{2})} = \frac{a^{2} - c^{2}}{b^{2}}$ .

Vậy $\cos \hat{(A C, B D)} = |\frac{a^{2} - c^{2}}{b^{2}}|$ .

Câu 43:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 1}{1}$ và mặt cầu $(S) : {(x - 4)}^{2} + {(y - 5)}^{2} + {(z - 7)}^{2} = 2$ . Hai điểm A và B thay đổi trên (S) sao cho tiếp diện của tại A và B vuông góc với nhau. Đường thẳng qua A song song với d cắt mặt phẳng (Oxy) tại M, đường thẳng B song song với d cắt mặt phẳng (Oxy) tại N. Giá trị lớn nhất của tổng AM+BN bằng

A. $16 \sqrt{6}$

B. $8 \sqrt{6}$

C. $7 \sqrt{6} + 5 \sqrt{3}$

D. $\sqrt{20}$

Xem đáp án

Trong không gian Oxyz, cho đường thẳng d: x-1/2=y/1=z-1/1 và mặt cầu (ảnh 4)

Trong không gian Oxyz, cho đường thẳng d: x-1/2=y/1=z-1/1 và mặt cầu (ảnh 1)

Trong không gian Oxyz, cho đường thẳng d: x-1/2=y/1=z-1/1 và mặt cầu (ảnh 2)

Trong không gian Oxyz, cho đường thẳng d: x-1/2=y/1=z-1/1 và mặt cầu (ảnh 3)

Câu 44:

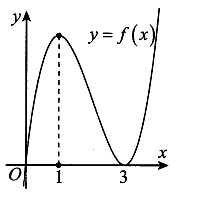
Cho hàm số y=f(x) có đồ thị như hình vẽ. Tất cả giá trị của tham số m để đồ thị hàm số $h (x) = |f^{2} (x) + f (x) + m|$ có đúng 3 điểm cực trị là

A. $m \geq \frac{1}{4}$

B. $m \geq 1$

C. $m < 1$

D. $m > \frac{1}{4}$

Xem đáp án

Xét hàm số $g (x) = f^{2} (x) + f (x) + m$ .

Ta có $g^{'} (x) = 2 f^{'} (x) f (x) + f^{'} (x) = f^{'} (x) (2 f (x) + 1)$ .

Dựa vào đồ thị của hàm số y=f(x) suy ra

$g^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} f^{'} (x) = 0 \\ f (x) = - \frac{1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 3 \\ x = a < 0 \end{array}$ .

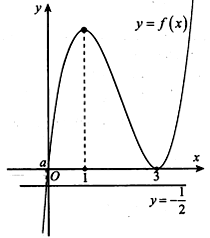
Cho hàm số y=f(x) có đồ thị như hình vẽ. Tất cả giá trị của tham số m (ảnh 1)

Ta có $g (a) = f^{2} (a) + f (a) + m = {(- \frac{1}{2})}^{2} - \frac{1}{2} + m = m - \frac{1}{4}$ và $g (3) = f^{2} (3) + f (3) + m = m$ .

Bảng biến thiên của hàm số y = g(x)

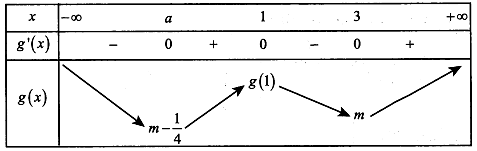
Cho hàm số y=f(x) có đồ thị như hình vẽ. Tất cả giá trị của tham số m (ảnh 2)

Đồ thị hàm số y=h(x) có đúng 3 điểm cực trị khi và chỉ khi $m - \frac{1}{4} \geq 0 \Leftrightarrow m \geq \frac{1}{4}$ .

Câu 45:

Cho đồ thị $(C_{1}) : y = \frac{- 3 x + 5}{x - 2}$ ; $(C_{2}) : \frac{- 3 x + 2}{x - 2}$ và điểm $I (2; - 3)$ . Lấy $A, B \in (C_{1})$ , các tia đối của tia IA, IB cắt $(C_{2})$ lần lượt tại C và D sao cho $S_{A B C D} = 2020$ . Diện tích tam giác IAB bằng

A. $\frac{505}{2}$

B. 250

C. $\frac{2020}{9}$

D. 505

Xem đáp án

Ta có $\{\begin{cases} (C_{1}) : y = - 3 - \frac{1}{x - 2} \\ (C_{2}) : y = - 3 - \frac{4}{x - 2} \end{cases}$

Lấy $A (a + 2; - 3 - \frac{1}{a}) \in (C_{1}); C (c + 2; - 3 - \frac{4}{c}) \in C_{2} \Rightarrow \vec{I C} = (c; - \frac{4}{c})$ .

Mà I, A, C thẳng hàng nên

\{\begin{cases} 2 I A = I C \\ 2 I B = I D \end{cases} \Rightarrow S_{A B C D} = 9 S_{Δ I A B} \Rightarrow S_{Δ I A B} = \frac{2020}{9}

.

Câu 46:

Cho phương trình $\log_{\sqrt{2}} (x^{3} - 3 x) = 2 \sin (m x)$ với m là tham số thực. Có tất cả bao nhiêu giá trị của $m \in (- 2020; 2020)$ để phương trình đã cho có nghiệm trên đoạn [2;4]?

A. 1280

B. 1285

C. 1287

D. 1286

Xem đáp án

Câu 47:

Cho $f (x)$ là hàm số chẵn liên tục trong đoạn $[- 1; 1]$ và $\int_{- 1}^{1} f (x) d x = 2$ . Giá trị tích phân $I = \int_{-}^{1} \frac{f (x) + 2020}{1 + e^{x}} d x$ là

A. I = 2019

B. I = 2020

C. I=2021

D. I= 2018

Xem đáp án

$I = \int_{- 1}^{1} \frac{f (x) + 2020}{1 + e^{x}} d x = \int_{- 1}^{0} \frac{f (x) + 2020}{1 + e^{x}} d x + \int_{0}^{1} \frac{f (x) + 2020}{1 + e^{x}} d x = I_{1} + I_{2}$

Xét $I_{1} = \int_{- 1}^{0} \frac{f (x) + 2020}{1 + e^{x}} d x$ . Đặt $x = - t \Rightarrow d x = - d t$ , đổi cận $x = 0 \Rightarrow t = 0, x = - 1 \Rightarrow t = 1$ .

$I_{1} = \int_{1}^{0} \frac{f (- t) + 2020}{1 + e^{- t}} (- d t) = \int_{0}^{1} \frac{e^{t} [f (t) + 2020]}{1 + e^{t}} d t$

Ta có $\int_{0}^{1} \frac{e^{t} [f (t) + 2020]}{1 + e^{t}} d t = \int_{0}^{1} \frac{e^{x} [f (x) + 2020]}{1 + e^{x}} d x$ .

Suy ra $I = \int_{- 1}^{1} \frac{f (x) + 2020}{1 + e^{x}} d x = \int_{0}^{1} \frac{e^{x} [f (x) + 2020]}{1 + e^{x}} d x + \int_{0}^{1} \frac{f (x) + 2020}{1 + e^{x}} d x$

$= \int_{0}^{1} \frac{(1 + e^{x}) [f (x) + 2020]}{1 + e^{x}} d x = \int_{0}^{1} [f (x) + 2020] d x = \frac{1}{2} \int_{- 1}^{1} [f (x) + 2020] d x = 2021$ .

Câu 48:

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ có bảng biến thiên như sau.

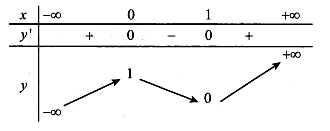
Tìm m để phương trình $|f (x)| = m$ có bốn nghiệm phân biệt $x_{1} < x_{2} < x_{3} < \frac{1}{2} < x_{4}$ .

A. $\frac{1}{2} < m < 1$

B. $0 < m < 1$

C. $0 < m \leq 1$

D. $\frac{1}{2} \leq m < 1$

Xem đáp án

Ta có $\{\begin{cases} f (0) = 1 \\ f (1) = 0 \\ f^{'} (0) = 0 \\ f^{'} (1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = - 3 \\ c = 0 \\ d = 1 \end{cases}$ , suy ra $y = f (x) = 2 x^{3} - 3 x^{2} + 1$ .

Nhận xét $f (x) = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - \frac{1}{2} \end{array}$ . Bảng biến thiên của hàm số $y = |f (x)|$ như sau:

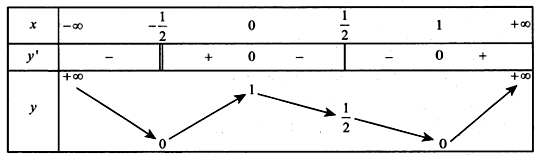
Cho hàm số y=f(x): ax^3+bx^2+cx+d có bảng biến thiên như sau. (ảnh 2)

Dựa vào bảng biến thiên suy ra phương trình $|f (x)| = m$ có nghiệm phân biệt $x_{1} < x_{2} < x_{3} < \frac{1}{2} < x_{4}$ khi và chỉ khi $\frac{1}{2} < m < 1$ .

Câu 49:

Cho ba điểm A, B, C lần lượt là 3 điểm biểu diễn của các số phức $z_{1}, z_{2}, z_{3}$ thỏa mãn điều kiện $|z_{1}| = |z_{2}| = |z_{3}| = 9$ và $z_{1} + z_{2} = 8 + 6 i$ . Giá trị lớn nhất của diện tích tam giác ABC bằng

A. $28 \sqrt{14}$

B. $28 \sqrt{17}$

C. $30 \sqrt{14}$

D. $30 \sqrt{17}$

Xem đáp án

Ta có $z_{1} + z_{2} = 8 + 6 i$ nên trung điểm của AB là điểm $M (4; 3)$ và ba điểm A, B, C thuộc đường tròn (0;9). Ta hạ CH vuông góc AB và hạ OK vuông góc CH.

Khi đó:

$S = \frac{1}{2} C H . A B = (C K + K H) \sqrt{O A^{2} - O M^{2}} \Leftrightarrow S = 2 \sqrt{14} (C K + 5) \leq 2 \sqrt{14} (C O + 5) = 28 \sqrt{14}$ .

Câu 50:

Trong không gian Oxyz, cho điểm A(0;0;6) , điểm M nằm trên mặt phẳng (Oxy) và

M \neq O

. Gọi D là hình chiếu vuông góc của O lên AM và E là trung điểm của OM. Biết đường thẳng DE luôn tiếp xúc với một mặt cầu cố định. Bán kính mặt cầu đó là

A. R=2

B. R=1

C. R=3

D. $R = \sqrt{2}$

Xem đáp án

Ta có 0A=6.

Tam giác OAM luôn vuông tại O. Gọi I là trung điểm của OA (điểm I cố định).

Ta có tam giác ADO vuông tại D có ID là đường trung tuyến nên $I D = \frac{1}{2} O A = 3$ . (1)

Ta có IE là đường trung bình của tam giác OAM nên IE song song với AM.

Mặt khác $O D ⊥ A M \Rightarrow O D ⊥ I E$ .

Lại có tam giác EOD cân tại E. Từ đó suy ra IE là đường trung trực của OD.

Do đó $\hat{D O E} = \hat{O D E}, \hat{I OD} = \hat{I D O} \Rightarrow \hat{I D E} = \hat{I O E} = 90 ° \Rightarrow I D ⊥ D E$ . (2)

Từ (1) và (2), suy ra DE luôn tiếp xúc với mặt cầu tâm I bán kính $R = \frac{O A}{2} = 3$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết

25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết (Đề 5)

Danh sách câu hỏi

Bài thi liên quan