Góc giữa hai mặt phẳng
-
501 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình chóp S.ABC có đáy ABC. là tam giác vuông tại B, BC=a. Cạnh bên SA=a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng \[{45^0}\]. Độ dài AC bằng
 Xem đáp án
Xem đáp án
Ta có\[\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow BC\] là giao tuyến.
Mặt khác\[SA \bot \left( {ABC} \right)\] và\[{\rm{\Delta }}ABC\] vuông tại\[B \Rightarrow AB \bot BC\]
Nên \(\left\{ {\begin{array}{*{20}{c}}{SA \bot BC}\\{AB \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)
\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABC) = BC}\\{(SBC) \supset SB \bot BC}\\{(ABC) \supset AB \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABC)}) = (\widehat {SB;AB}) = \widehat {SBA} = {45^0}\)
Xét\[\;{\rm{\Delta }}SAB\] vuông tại A, có\[\widehat {SBA} = {45^0} \Rightarrow SA = AB = a\]
Mà\[A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \]
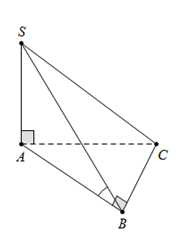
Đáp án cần chọn là: A
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh aa. Cạnh bên \(SA = a\sqrt 3 \) và vuông góc với mặt đáy (ABC). Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi M là trung điểm của BC, suy ra\[AM \bot BC\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{AM \bot BC}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAM) \Rightarrow BC \bot SM\)
\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABC) = BC}\\{(SBC) \supset SM \bot BC}\\{(ABC) \supset AM \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABC)}) = (\widehat {SM;AM}) = \widehat {SMA}.\)
Tam giác ABC đều cạnh a, suy ra trung tuyến\[AM = \frac{{a\sqrt 3 }}{2}.\]
Tam giác vuông SAM có\[\sin \widehat {SMA} = \frac{{SA}}{{SM}} = \frac{{SA}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{2\sqrt 5 }}{5}.\]
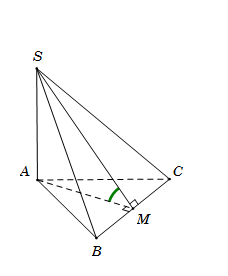
Đáp án cần chọn là: D
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{a\sqrt 3 }}{2}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
 Xem đáp án
Xem đáp án
Gọi Q là trung điểm BC, suy ra \[OQ \bot BC\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot OQ}\\{BC \bot SO}\end{array}} \right. \Rightarrow BC \bot (SOQ) \Rightarrow BC \bot SQ\)
Do đó
\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABCD) = BC}\\{(SBC) \supset SQ \bot BC}\\{(ABCD) \supset OQ \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABCD)}) = (\widehat {SQ;OQ}) = \widehat {SQ}\)
Tam giác vuông SOQ, có\[\tan \widehat {SQO} = \frac{{SO}}{{OQ}} = \sqrt 3 \Rightarrow \widehat {SQO} = {60^0}\]
Vậy mặt phẳng (SBC) hợp với mặt đáy (ABCD) một góc \({60^0}\).
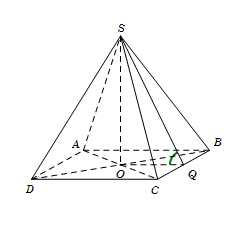
Đáp án cần chọn là: C
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, các cạnh \[SA = SB = a,\;SD = a\sqrt 2 \]. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng \({90^0}\). Độ dài đoạn thẳng BD
 Xem đáp án
Xem đáp án
Gọi I là tâm của hình thoi ABCD.
Và H là hình chiếu vuông góc của S lên BD.
\[\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = {90^0} \Rightarrow \left( {SBD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)\]
Khi đó\(\left\{ {\begin{array}{*{20}{c}}{SH \bot AC}\\{BD \bot AC}\end{array}} \right. \Rightarrow AC \bot (SBD) \Rightarrow AC \bot SI\)
Mà I là trung điểm của\[AC \Rightarrow {\rm{\Delta }}SAC\] cân tại S\[ \Rightarrow SA = SB = SC = BC = a\]
\[{\rm{\Delta }}SAC = {\rm{\Delta }}BAC\left( {c.c.c} \right) \Rightarrow BI = SI = \frac{1}{2}BD \Rightarrow {\rm{\Delta }}SBD\] vuông tại S
\[ \Rightarrow B{D^2} = S{B^2} + S{D^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow BD = a\sqrt 3 \]
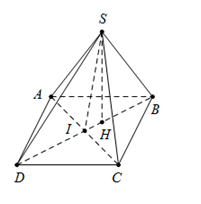
Đáp án cần chọn là: C
Câu 5:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \[A,\widehat {ABC} = {60^0}\], tam giác SBC là tam giác đều có bằng cạnh 2a và nằm trong mặt phẳng vuông với đáy. Gọi φ là góc giữa hai mặt phẳng (SAC) và (ABC). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi H là trung điểm của BC, suy ra \[SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)\].
Gọi K là trung điểm AC, suy ra \[HK//AB\] nên \[HK \bot AC\].
Ta có\(\left\{ {\begin{array}{*{20}{c}}{AC \bot HK}\\{AC \bot SH}\end{array}} \right. \Rightarrow AC \bot (SHK) \Rightarrow AC \bot SK\)
\(\left\{ {\begin{array}{*{20}{c}}{(SAC) \cap (ABC) = AC}\\{(SAC) \supset SK \bot AC}\\{(ABC) \supset HK \bot AC}\end{array}} \right. \Rightarrow (\widehat {(SAC);(ABC)}) = (\widehat {SK;HK}) = \widehat {SKH}\)
Tam giác vuông ABC, có\[AB = BC.\cos \widehat {ABC} = a \Rightarrow HK = \frac{1}{2}AB = \frac{a}{2}.\]
Tam giác SBC đều cạnh 2a có đường cao\[SH = \frac{{2a\sqrt 3 }}{2}\]
Tam giác vuông SHK, có \[\tan \widehat {SKH} = \frac{{SH}}{{HK}} = \frac{{\frac{{2a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = 2\sqrt 3 \]
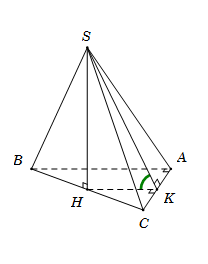
Đáp án cần chọn là: B
Câu 6:
Cho hình lăng trụ tứ giác đều ABCD.A′B′C′D′ có đáy cạnh bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC′) có số đo bằng \({60^0}\). Độ dài cạnh bên của hình lăng trụ bằng
 Xem đáp án
Xem đáp án
Vì\[ABCD.A'B'C'D'\] là lăng trụ tứ giác đều
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AB \bot BB\prime }\\{AB \bot BC}\end{array}} \right. \Rightarrow AB \bot (BB\prime C\prime B) \Rightarrow AB \bot BC\prime \)
\(\left\{ {\begin{array}{*{20}{c}}{(ABC\prime ) \cap (ABCD) = AB}\\{(ABC\prime ) \supset BC\prime \bot AB}\\{(ABCD) \supset BC \bot AB}\end{array}} \right. \Rightarrow (\widehat {(ABC\prime );(ABCD)}) = (\widehat {BC\prime ;BC}) = \widehat {C\prime BC} = {60^0}\)
Tam giác BCC′ vuông tại C, có\[\tan \widehat {C'BC} = \frac{{CC'}}{{BC}} \Rightarrow CC' = \tan {60^0}.a = a\sqrt 3 .\]
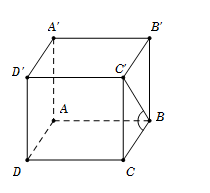
Đáp án cần chọn là: C
Câu 7:
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng aa. Gọi M là trung điểm SC. Tính góc \[\varphi \] giữa hai mặt phẳng (MBD) và (ABCD).
 Xem đáp án
Xem đáp án
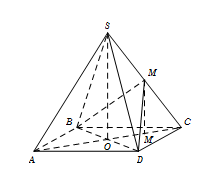
Gọi M’ là trung điểm\[OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).\]
Theo công thức diện tích hình chiếu, ta có\[{S_{{\rm{\Delta }}{\kern 1pt} M'BD}} = \cos \varphi .{S_{{\rm{\Delta }}{\kern 1pt} MBD}}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow \cos \varphi = \frac{{{S_{{\rm{\Delta }}{\kern 1pt} M'BD}}}}{{{S_{{\rm{\Delta }}{\kern 1pt} MBD}}}} = \frac{{BD.M'O}}{{BD.MO}} = \frac{{M'O}}{{MO}} = \frac{{\frac{1}{2}OC}}{{\frac{1}{2}SA}}}\\{ = \frac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \frac{{\sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = {{45}^0}.}\end{array}\]
Đáp án cần chọn là: C
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc \(\widehat {BAD} = {60^0},SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi \[\varphi \] là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Từ giả thiết suy ra tam giác ABD đều cạnh aa.
Gọi H là hình chiếu của SS trên mặt phẳng (ABCD).
Do SA=SB=SD nên suy ra H là tâm của tam gác đều ABD.
Suy ra
\[AH = \frac{2}{3}AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3},HI = \frac{1}{3}AI = \frac{1}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\]
và\[SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{6}.\]
Vì ABCD là hình thoi nên \[HI \bot BD\]. Tam giác SBD cân tại S nên\[SI \bot BD\]. Do đó\[\widehat {\left( {SBD} \right);\left( {ABCD} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIH}.\]
Trong tam vuông SHI, có\[\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 .\]
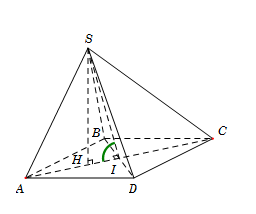
Đáp án cần chọn là: A
Câu 9:
Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H, K lần lượt là trung điểm của AB, CD. Gọi φ là góc giữa hai mặt phẳng (SAB) và (SCD). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Dễ dàng xác định giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua S và song song với AB và CD.
Trong mặt phẳng (SAB) có\[SH \bot AB \Rightarrow SH \bot d.\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{CD \bot HK}\\{CD \bot SH}\end{array}} \right. \Rightarrow CD \bot (SHK) \Rightarrow CD \bot SK \Rightarrow d \bot SK\)
Từ đó suy ra
\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \cap (SCD) = d}\\{(SAB) \supset SH \bot d}\\{(SCD) \supset SK \bot d}\end{array}} \right. \Rightarrow (\widehat {(SAB);(SCD)}) = (\widehat {SH;SK}) = \widehat {HSK}\)
Trong tam giác vuông SHK, có\[\tan \widehat {HSK} = \frac{{HK}}{{SH}} = \frac{a}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{2\sqrt 3 }}{3}.\]
Đáp án cần chọn là: B
Câu 10:
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi \[\varphi \] là góc giữa hai mặt phẳng (SBD) và (SCD). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi\[O = AC \cap BD\]. Do hình chóp S.ABCD đều nên \[SO \bot \left( {ABCD} \right)\]
Gọi M là trung điểm của SD. Tam giác SCD đều nên\[CM \bot SD\]
Tam giác SBD có\[SB = SD = a,BD = a\sqrt 2 \]
Suy ra\[{\rm{\Delta }}\,SBD\] vuông tại\[S \Rightarrow SB \bot SD \Rightarrow OM \bot SD.\]
Do đó
\(\left\{ {\begin{array}{*{20}{c}}{(SBD) \cap (SCD) = SD}\\{(SBD) \supset OM \bot SD}\\{(SCD) \supset CM \bot SD}\end{array}} \right. \Rightarrow ((\widehat {SBD);(SCD})) = (\widehat {OM;CM}) = \widehat {OM}\)
Ta có\(\left\{ {\begin{array}{*{20}{c}}{OC \bot BD}\\{OC \bot SO}\end{array}} \right. \Rightarrow OC \bot (SBD) \Rightarrow OC \bot OM\)
Tam giác vuông MOC vuông tại O, có\[\tan \widehat {CMO} = \frac{{OC}}{{OM}} = \frac{{\frac{1}{2}a\sqrt 2 }}{{\frac{1}{2}a}} = \sqrt 2 \]
Đáp án cần chọn là: D
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi E,F lần lượt là trung điểm của cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là
 Xem đáp án
Xem đáp án
Gọi (d) là đường thẳng đi qua S và song song với E.
Vì EF là đường trung bình tam giác ABC suy ra EF // BC.
Khi đó d // EF // BC\[ \Rightarrow \left( {SEF} \right) \cap \left( {SBC} \right) = \left( d \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right).\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{SA \bot BC(SA \bot (ABC))}\\{AB \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{BC \bot SE}\\{BC \bot SB}\end{array}} \right.\,\,\,\,\left( 2 \right)\)
Từ (1),(2) suy ra\(\left\{ {\begin{array}{*{20}{c}}{(d) \bot SE}\\{(d) \bot SB}\end{array}} \right. \Rightarrow (\widehat {(SEF);(SBC)}) = (\widehat {SE;SB}) = \widehat {BSE}\)
Đáp án cần chọn là: C
Câu 12:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 600. Tính độ dài đường cao SHcủa khối chóp.
 Xem đáp án
Xem đáp án
Gọi H là chân đường cao kẻ từ đỉnh S xuống mặt phẳng (ABC).
Vì S.ABC là hình chóp đều có SA = SB = SC nên suy ra H chính là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi M là trung điểm của BC, ta có
\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AM}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot (SAM) \Rightarrow BC \bot SM\)
Khi đó
\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABC) = BC}\\{(SBC) \supset SM \bot BC}\\{(ABC) \supset AM \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABC)}) = (\widehat {SM;AM}) = \widehat {SMA} = {60^0}\)
Tam giác ABC đều cạnh a có \[AM = \frac{{a\sqrt 3 }}{2} \Rightarrow HM = \frac{{AM}}{3} = \frac{{a\sqrt 3 }}{6}.\]
Tam giác AHM vuông tại H, có\[SH = \tan {60^0}.\frac{{a\sqrt 3 }}{6} = \frac{a}{2}.\]
Vậy độ dài đường cao\[SH = \frac{a}{2}.\]
Đáp án cần chọn là: C
Câu 13:
Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, AB=2a, AD=CD=a. Cạnh bên SA=a và vuông góc với mặt phẳng (ABCD). Gọi \[\varphi \] là góc giữa hai mặt phẳng (SBC) và (ABCD) . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi M là trung điểm AB ⇒ADCM là hình vuông.
Vì\[\,CM = AD = a = \frac{{AB}}{2}\] Suy ra tam giác ACB có trung tuyến bằng nửa cạnh đáy nên vuông tại C.
Ta có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AC}\end{array}} \right. \Rightarrow BC \bot (SAC) \Rightarrow BC \bot SC\)
Do đó :
\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABCD) = BC}\\{(SBC) \supset SC \bot BC}\\{(ABCD) \supset AC \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABCD)}) = (\widehat {SC;AC}) = \widehat {SCA}\)
Tam giác SAC vuông tại A\[ \Rightarrow \tan \varphi = \frac{{SA}}{{AC}} = \frac{{SA}}{{\sqrt {A{D^2} + C{D^2}} }} = \frac{a}{{a\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\]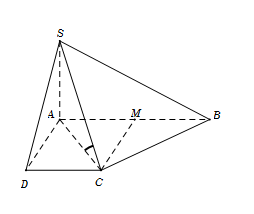
Đáp án cần chọn là: A
Câu 14:
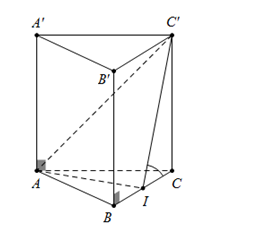
Cho hình lăng trụ đứng ABC.A′B′C′, đáy ABC là tam giác đều a. Gọi I là trung điểm của BC. Góc giữa hai mặt phẳng (C′AI) và (ABC) bằng 600. Độ dài AA′ bằng
 Xem đáp án
Xem đáp án
Ta có I là trung điểm của \[BC\,\, \Rightarrow AI \bot BC\]
\[ABC.A'B'C'\] là lăng trụ đứng \[ \Rightarrow C'C \bot \left( {ABC} \right).\]
\[ \Rightarrow C'C \bot AI\] mà\[AI \bot BC \Rightarrow AI \bot \left( {BCC'B'} \right) \Rightarrow AI \bot C'I\]
Suy ra
\(\left\{ {\begin{array}{*{20}{c}}{(C\prime AI) \cap (ABC) = AI}\\{(C\prime AI) \supset C\prime I \bot AI}\\{(ABC) \supset BC \bot AI}\end{array}} \right. \Rightarrow (\widehat {(C\prime AI);(ABC)}) = (\widehat {C\prime I;BC}) = \widehat {C\prime IC} = {60^0}\)
Xét \[{\rm{\Delta }}\,C'CI\] vuông tại C, có :
\[\tan \widehat {C'IC} = \frac{{CC'}}{{IC}} \Rightarrow CC' = \tan {60^0}.\frac{a}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AA' = \frac{{a\sqrt 3 }}{2}\]
Đáp án cần chọn là: A
Câu 15:
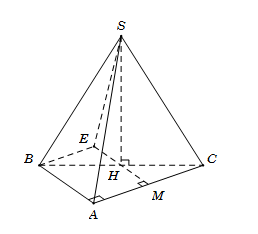
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=AC=a. Hình chiếu vuông góc HH của SS trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC và \(SH = \frac{{a\sqrt 6 }}{2}\). Gọi \[\varphi \] là góc giữa hai đường thẳng SB và AC. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi H là trung điểm BC. Tam giác ABC vuông tại A nên H trung điểm của BC.
Theo giả thiết, ta có \[SH \bot \left( {ABC} \right)\]
Qua B kẻ\[Bx//AC\] . Khi đó \[\widehat {\left( {SB;AC} \right)} = \widehat {\left( {SB;Bx} \right)}\]
Kẻ\[HE \bot Bx\] tại E, cắt AC tại M
Suy ra AMEB là hình chữ nhật nên\(\left\{ {\begin{array}{*{20}{c}}{BE = AM = \frac{1}{2}AC = \frac{a}{2}}\\{HE = HM = \frac{1}{2}AB = \frac{a}{2}}\end{array}} \right.\)
Ta có\(\left\{ {\begin{array}{*{20}{c}}{Bx \bot HE}\\{Bx \bot SH}\end{array}} \right. \Rightarrow Bx \bot (SHE) \Rightarrow Bx \bot SE\)
Tam giác vuông SEB vuông tại E, có\[\cot \widehat {SBE} = \frac{{BE}}{{SE}} = \frac{{AM}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{\frac{a}{2}}}{{\sqrt {\frac{{6{a^2}}}{4} + \frac{{{a^2}}}{4}} }} = \frac{{\sqrt 7 }}{7}\]
Đáp án cần chọn là: C
Câu 16:
Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên các đường thẳng vuông góc với mặt phẳng (P) tại B và C lấy điểm D,E cùng phía so với (P) sao cho \(BD = \frac{{a\sqrt 3 }}{2}\) và \(CE = a\sqrt 3 \).Tính góc giữa hai mặt phẳng (ADE) và (ABC).
 Xem đáp án
Xem đáp án
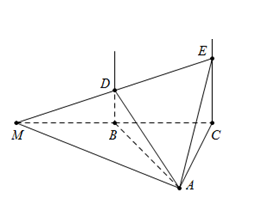
Vẽ\[BC \cap DE = M \Rightarrow \left( {ADE} \right) \cap \left( {ABC} \right) = AM\]
Ta có\[BD//CE \Rightarrow \frac{{BD}}{{CE}} = \frac{{MB}}{{MC}} = \frac{1}{2} \Rightarrow BM = BC = BA\]
Suy ra \[{\rm{\Delta }}AMC\] vuông tại \[A \Rightarrow AM \bot AC\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AM \bot AC}\\{AM \bot EC}\end{array}} \right. \Rightarrow AM \bot (ACE) \Rightarrow AM \bot AE \Rightarrow \Delta AME\) vuông tại AA.
Mặt khác ta có:
\(\left\{ {\begin{array}{*{20}{c}}{(ADE) \cap (ABC) = AM}\\{(ADE) \supset AE \bot AM}\\{(ABC) \supset AC \bot AM}\end{array}} \right. \Rightarrow \widehat {\left( {\left( {ADE} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {AE;AC} \right)} = \widehat {EAC}\)
Xét \[{\rm{\Delta }}AEC\] vuông tại C, có\[\tan \widehat {EAC} = \frac{{EC}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {EAC} = {60^0}\]
Đáp án cần chọn là: C
Câu 17:
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a,CD=2x. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
 Xem đáp án
Xem đáp án
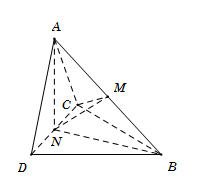
Gọi M,N lần lượt là trung điểm của AB,CD.
Ta có \[AN \bot CD\] mà\[\left( {ACD} \right) \bot \left( {BCD} \right)\]
\[ \Rightarrow AN \bot \left( {BCD} \right) \Rightarrow AN \bot BN \Rightarrow {\rm{\Delta }}ANB\] vuông tại N \[ \Rightarrow NM = \frac{{AB}}{2}\,\,\left( 1 \right)\]Tam giác ABC cân tại C, có M là trung điểm của AB \[ \Rightarrow CM \bot AB.\]
Giả sử \[\left( {ABC} \right) \bot \left( {ABD} \right)\]mà\[CM \bot AB \Rightarrow CM \bot \left( {ABD} \right) \Rightarrow CM \bot DM.\]
Khi đó, \[{\rm{\Delta }}\,MCD\] vuông tại M. Ta có
\[{\rm{\Delta }}ABC = {\rm{\Delta }}ABD\,\,\left( {c.c.c} \right) \Rightarrow CM = DM \Rightarrow {\rm{\Delta }}MCD\] vuông cân tại M.
\[ \Rightarrow \,\,MN = \frac{{CD}}{2}\,\,\,\left( 2 \right)\]Từ (1) và (2)\[ \Rightarrow AB = CD = 2x\]
Lại có
\[{\rm{\Delta }}ACD = {\rm{\Delta }}BCD\,\,\left( {c.c.c} \right) \Rightarrow AN = BN = \sqrt {A{C^2} - C{N^2}} = \sqrt {{a^2} - {x^2}} ,\]
mà\[A{B^2} = A{N^2} + B{N^2}.\]
Suy ra\[2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2} \Leftrightarrow x = \frac{{a\sqrt 3 }}{3}.\]
Đáp án cần chọn là: A
Câu 18:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Gọi H là trung điểm AB. Biết rằng SH vuông góc với mặt phẳng (ABC) và AB=SH=a. Tính cosin của góc α tọa bởi hai mặt phẳng (SAB) và (SAC).
 Xem đáp án
Xem đáp án
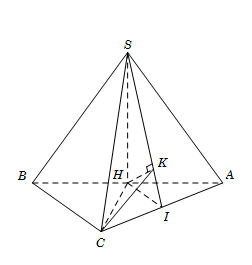
Ta có \[SH \bot \left( {ABC} \right) \Rightarrow SH \bot CH\](1)
Tam giác ABC cân tại C nên \[CH \bot AB\](2)
Từ (1) và (2), suy ra\[CH \bot \left( {SAB} \right)\]
Gọi I là trung điểm \[AC \Rightarrow \,\,HI//BC\mathop \to \limits^{BC{\kern 1pt} \bot {\kern 1pt} {\kern 1pt} AC} HI \bot AC\](3)
Mặt khác\[AC \bot SH\] (do \[SH \bot \left( {ABC} \right)\])(4)
Từ (3) và (4), suy ra \[AC \bot \left( {SHI} \right)\]
Kẻ\[HK \bot SI\,\left( {K \in SI} \right)\](5)
Từ \[AC \bot \left( {SHI} \right) \Rightarrow AC \bot HK\](6)
Từ (5) và (6), suy ra \[HK \bot \left( {SAC} \right)\]
Vì\(\left\{ {\begin{array}{*{20}{c}}{HK \bot (SAC)}\\{HC \bot (SAB)}\end{array}} \right.\) nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC
Ta có \[HK \bot \left( {SAC} \right) \Rightarrow HK \bot CK \Rightarrow {\rm{\Delta }}CHK\] vuông tại KDo đó góc giữa hai mặt phẳng (SAC) và (SAB) là\[\widehat {CHK}\]Có\[CH = \frac{1}{2}AB = \frac{a}{2}\]
\[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{1}{2}.\frac{a}{{\sqrt 2 }}} \right)}^2}}} \Rightarrow HK = \frac{a}{3}\]
Do đó\[\cos \widehat {CHK} = \frac{{HK}}{{CH}} = \frac{{\frac{a}{3}}}{{\frac{a}{2}}} = \frac{2}{3}.\]Đáp án cần chọn là: D
Câu 19:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=x và vuông góc với mặt phẳng (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 600.
 Xem đáp án
Xem đáp án
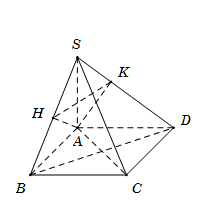
Từ A kẻ AH vuông góc với SB\[\,\left( {H \in SB} \right).\]
Ta có \(\left\{ {\begin{array}{*{20}{c}}{SA \bot BC}\\{AB \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\) mà\[AH \bot SB\] suy ra\[AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\]
Từ A kẻ AK vuông góc với\[SD\,\,\,\left( {K \in SD} \right),\] tương tự, chứng minh được\[AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC\]
Khi đó\[SC \bot \left( {AHK} \right)\] suy ra
\[\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK} = {60^0}.\]
Lại có\[{\rm{\Delta }}\,SAB = {\rm{\Delta }}\,SAD\,\,\left( {c.g.c} \right) \Rightarrow AH = AK\] mà \[\widehat {HAK} = {60^0}\]suy ra tam giác AHK đều.
Tam giác SAB vuông tại A có
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{x^2}}} + \frac{1}{{{a^2}}} \Rightarrow AH = \frac{{xa}}{{\sqrt {{x^2} + {a^2}} }} = AK = HK\]
Suy ra
\[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{x^2} - \frac{{{x^2}{a^2}}}{{{x^2} + {a^2}}}} = \frac{{{x^2}}}{{\sqrt {{x^2} + {a^2}} }} \Rightarrow \frac{{SH}}{{SB}} = \frac{{{x^2}}}{{{x^2} + {a^2}}}.\]
Tương tự ta chứng minh được\[\frac{{SK}}{{SC}} = \frac{{{x^2}}}{{{x^2} + {a^2}}}\]
⇒HK//BD suy ra
\[\frac{{SH}}{{SB}} = \frac{{HK}}{{BD}} \Leftrightarrow \frac{{{x^2}}}{{{x^2} + {a^2}}} = \frac{{xa}}{{\sqrt {{x^2} + {a^2}} .a\sqrt 2 }} \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {a^2}} }} = \frac{1}{{\sqrt 2 }} \Leftrightarrow 2{x^2} = {x^2} + {a^2} \Rightarrow x = a.\]
Đáp án cần chọn là: C
Câu 20:
Đường thẳng CD vuông góc với mặt phẳng
 Xem đáp án
Xem đáp án
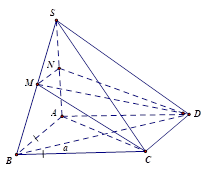
ABCD là hình vuông\[ \Rightarrow CD \bot AD\] (1)
Ta có \[SA \bot \left( {ABCD} \right) \Rightarrow CD \bot SA\] (2)
Từ ( 1) và (2) suy ra \[CD \bot \left( {SAD} \right)\].
Đáp án cần chọn là: C
Câu 21:
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \) cạnh bên AA′=a (minh họa như hình vẽ). Góc giữa hai mặt phẳng (A′BD) và (C′BD) bằng bao nhiêu độ?
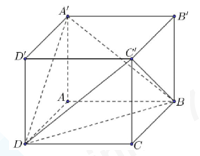
 Xem đáp án
Xem đáp án
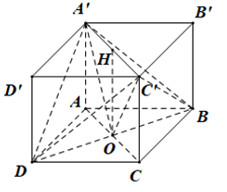
Bước 1: Xác định góc
Vì ABCD là hình vuông nên AC vuông góc BD tại O.
Suy ra \[BD \bot \left( {A'OC'} \right)\]. Góc giữa hai mặt phẳng\[\left( {A'BD} \right),\,\,\left( {C'BD} \right)\] là\[\angle A'OC'\]
Bước 2: Sử dụng tính chất tam giác vuông cân để tính góc.
Gọi H là tâm hình vuông A′B′C′D′ thì H là trung điểm A′C′ và\[\begin{array}{*{20}{l}}{OH = A'A = a}\\{A'H = HC' = \frac{{A'C'}}{2} = \frac{{A'B'\sqrt 2 }}{2} = \frac{{a\sqrt 2 .\sqrt 2 }}{2} = a}\end{array}\]
Suy ra các tam giác\[OHA';\,\,OHC'\] vuông cân và\[\angle A'OC' = {90^ \circ }\]
Câu 22:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB=BC=2a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC), \(SA = \sqrt 3 a\). Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
 Xem đáp án
Xem đáp án
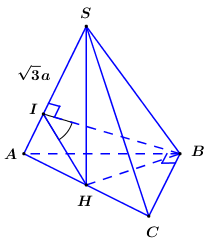
Bước 1: Gọi H là trung điểm của AC, chứng minh\[SH \bot \left( {SAC} \right),\,\,BH \bot \left( {SAC} \right)\]
Gọi H là trung điểm của AC ta có\[SH \bot AC\] (do tam giác SAC cân tại S).
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(SAC) \bot (ABC) = AC}\\{AH \subset (SAC),AH \bot AC}\end{array}} \right. \Rightarrow AH \bot \left( {ABC} \right)\). Tương tự \[BH \bot \left( {SAC} \right)\]
Bước 2: Trong (SAB) kẻ\[BI \bot SA\] chứng minh \[\angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BH;HI} \right)\]
Trong (SAB) kẻ \[BI \bot SA\] ta có
\(\left\{ {\begin{array}{*{20}{c}}{SA \bot BI}\\{SA \bot BH(do\,BH \bot (SAC))}\end{array}} \right. \Rightarrow SA \bot (BHI) \Rightarrow SA \bot HI\)
\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \cap (SAC) = SA}\\{BI \subset (SAB),BI \bot SA}\\{HI \subset (SAC),HI \bot SA}\end{array}} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BI;HI} \right)\)
Bước 3: Sử dụng tính chất tam giác vuông cân, định lí Pytago, hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Vì\[BH \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BH \bot HI \Rightarrow {\rm{\Delta }}BHI\] vuông tại I.
Do đó\[\angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BH;HI} \right) = \angle BHI\]
Tam giác ABC vuông cân tại B có\[AB = BC = 2a\] nên\[BH = \frac{{AB}}{{\sqrt 2 }} = a\sqrt 2 ,AC = AB\sqrt 2 = 2\sqrt 2 a\]
Ta có: \[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {3{a^2} - 2{a^2}} = a\]
\[ \Rightarrow HI = \frac{{SH.AH}}{{SA}} = \frac{{a.\sqrt 2 a}}{{\sqrt 3 a}} = \frac{{\sqrt 6 a}}{3}\]Xét tam giác vuông BHI có\[\tan \angle BIH = \frac{{BH}}{{IH}} = \frac{{a\sqrt 2 }}{{\frac{{\sqrt 6 a}}{3}}} = \sqrt 3 \Rightarrow \angle BIH = {60^0}\]
Vậy góc giữa mặt phẳng (SAB) và (SAC) là 600
