Hai mặt phẳng vuông góc
-
624 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?
 Xem đáp án
Xem đáp án
Gọi d là đường thẳng qua M và vuông góc với (P). Do\[\left( P \right)\,\,\parallel \,\,\left( Q \right) \Rightarrow d \bot \left( Q \right)\]
Giả sử (R) là mặt phẳng chứa d. Mà\(\left\{ {\begin{array}{*{20}{c}}{d \bot (P)}\\{d \bot (Q)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(R) \bot (P)}\\{(R) \bot (Q)}\end{array}} \right.\)
Có vô số mặt phẳng (R) chứa d. Do đó có vô số mặt phẳng qua M, vuông góc với (P) và (Q).
Đáp án cần chọn là: D
Câu 2:
Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
A sai. Trong trường hợp a,b, c đồng phẳng.
C sai. Trong trường hợp a và b cắt nhau, mặt phẳng (a,b) chứa b nhưng không vuông góc với a.
D sai. Trong trường hợp a và b vuông góc nhau và chéo nhau, nếu \[\left( \alpha \right) \supset a,\left( \alpha \right)\,\parallel \,b\] và \[\left( \beta \right) \supset b,\left( \beta \right)\,\parallel \,a\] thì \[\left( \alpha \right)\,\parallel \,\left( \beta \right)\]
Đáp án cần chọn là: B
Câu 3:
Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
A sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
B sai. Qua một đường thẳng chưa chắc đã có mặt phẳng vuông góc với một đường thẳng cho trước (vì nếu hai đường thẳng đã cho không vuông góc với nhau thì không có mặt phẳng nào hết)
D sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Đáp án cần chọn là: C
Câu 4:
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
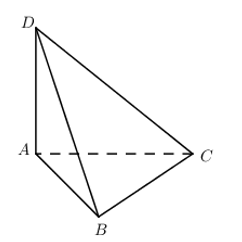
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{AD \bot AB}\\{AD \bot AC}\end{array}} \right. \Rightarrow AD \bot (ABC) \Rightarrow (ACD) \bot (ABC);(ABD) \bot (ABC)\\\left\{ {\begin{array}{*{20}{c}}{AC \bot AD}\\{AC \bot AB}\end{array}} \right. \Rightarrow AC \bot (ABD) \Rightarrow (ACD) \bot (ABD)\end{array}\)
⇒ A đúng.
\[AD \bot \left( {ABC} \right) \Rightarrow AD \bot BC\]Tương tự ta chứng minh được
\[AB \bot CD;\,\,AC \bot BD \Rightarrow D\]đúng.
Gọi H là trực tâm của tam giác BCD ta có
\(\left\{ {\begin{array}{*{20}{c}}{DH \bot BC}\\{AD \bot BC}\end{array}} \right. \Rightarrow BC \bot (ADH) \Rightarrow AH \bot BC\)
Tương tự ta chứng minh được\[AH \bot BD;\,\,AH \bot CD \Rightarrow AH \bot \left( {BCD} \right)\]⇒ B đúng.
Chưa đủ điều kiện để kết luận tam giác BCD vuông.
Đáp án cần chọn là: C
Câu 5:
Cho hình hộp đứng ABCD.A′B′C′D′ . Xét tất cả các hình bình hành có đỉnh là đỉnh của hình hộp đó. Hỏi có bao nhiêu hình bình hành mà mặt phẳng chứa nó vuông góc với mặt phẳng đáy (ABCD) ?
 Xem đáp án
Xem đáp án
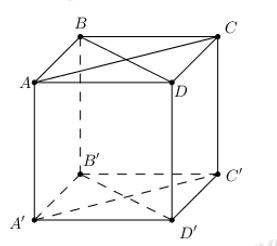
Có 6 hình bình hành thỏa mãn yêu cầu:\[ABB'A';\,\,BCC'B';\,\,CDD'C';\,\,ADD'A';\,\,ACC'A';\,\,BDD'B'\]
Đáp án cần chọn là: B
Câu 6:
Cho hình chóp S.ABC có \[SA \bot (ABC),\;\] tam giác ABC vuông tại B, kết luận nào sau đây sai?
 Xem đáp án
Xem đáp án
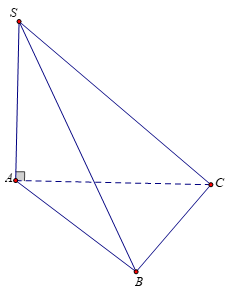
+) Nếu đáp án A đúng: \[\left( {SAC} \right) \bot \left( {SAB} \right)\]
Vì \[SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\]
Mà SA là giao tuyến của hai mặt phẳng vuông góc\[\left( {SAC} \right) \bot \left( {SAB} \right)\]
\[ \Rightarrow AB \bot \left( {SAC} \right) \Rightarrow AB \bot AC\] (Vô lý vì tam giác ABC vuông tại B.)
Vậy A sai.
+) Ta có:\(\left\{ {\begin{array}{*{20}{c}}{SA \bot (ABC)}\\{SA \subset (SAB),(SAC)}\end{array}} \right. \Rightarrow (SAB),(SAC) \bot (ABC)\) ⇒⇒ B, C đúng.
\[SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\] mà\[BC \bot ABBC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right)\]
\( \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\) ⇒ D đúng.
Đáp án cần chọn là: A
Câu 7:
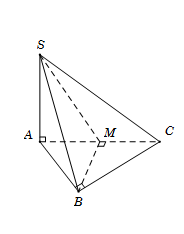
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với đáy. Gọi M là trung điểm AC. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Tam giác ABC cân tại B có M là trung điểm \[AC\,\, \Rightarrow \,\,BM \bot AC.\]
⇒ Đáp án A đúng.
Ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BM \bot AC}\\{BM \bot SA(doSA \bot (ABC))}\end{array}} \right. \Rightarrow BM \bot (SAC)\\ \Rightarrow (SBM) \bot (SAC)\end{array}\)
⇒ Đáp án B đúng.
Ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BC \bot BA}\\{BC \bot SA(doSA \bot (ABC))}\end{array}} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow (SBC) \bot (SAB)\end{array}\)
⇒ Đáp án C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Đáp án cần chọn là: D
Câu 8:
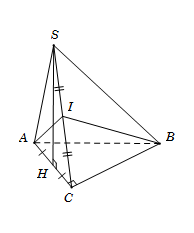
Cho tứ diện SABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác SBC đều, tam giác ABC vuông tại A. Gọi H, I lần lượt là trung điểm của BC và AB. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Do SBC là tam giác đều có H là trung điểm BC nên\[SH \bot BC\]
Mà\[\left( {SBC} \right) \bot \left( {ABC} \right)\] theo giao tuyến\[BC \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot AB.\]
⇒ Đáp án A đúng.
Ta có HI là đường trung bình của\[{\rm{\Delta }}\,ABC\] nên\[HI\parallel AC \Rightarrow HI \bot AB.\]
⇒ Đáp án B đúng.
Ta có\(\left\{ {\begin{array}{*{20}{c}}{SH \bot AB}\\{HI \bot AB}\end{array}} \right. \Rightarrow AB \bot (SHI) \Rightarrow (SAB) \bot (SHI)\)
⇒ Đáp án D đúng.
Dùng phương pháp loại trừ thì C là đáp án sai.

Đáp án cần chọn là: C
Câu 9:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I):\[AI \bot SC\]
\[(II):(SBC) \bot (SAC)\]
\[\;(III):AI \bot BC\]
\[(IV):(ABI) \bot (SBC)\]
 Xem đáp án
Xem đáp án
Tam giác SAC đều có I là trung điểm của SC nên \[AI \bot SC\].
⇒ Mệnh đề (I) đúng.
Gọi H là trung điểm AC suy ra \[SH \bot AC\]. Mà \[(SAC) \bot (ABC)\] theo giao tuyến AC nên \[SH \bot (ABC)\] do đó \[SH \bot BC\]. Hơn nữa theo giả thiết tam giác ABC vuông tại C nên \[BC \bot AC\].
Từ đó suy ra \[BC \bot (SAC) \Rightarrow BC \bot AI.\]. Do đó mệnh đề (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có : \(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BC \bot AC}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot (SAC)\\BC \subset (SBC) \Rightarrow (SBC) \bot (SAC)\end{array}\)
Vậy mệnh đề (II) đúng.
Vậy mệnh đề (II) đúng.
Đáp án cần chọn là: D
Câu 10:
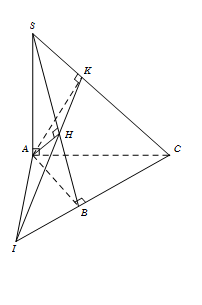
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại BB, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{SA \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\) Do đó A đúng.
Lại có \[AH \bot SB\] Từ đó suy ra\[AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\,\,\,\,\left( 1 \right)\]
Lại có theo giả thiết\[SC \bot AK\,\,\,\,\left( 2 \right)\]
Từ (1) và (2), suy ra \[SC \bot \left( {AHK} \right) \Rightarrow \left( {SBC} \right) \bot \left( {AHK} \right)\] Do đó B đúng.
Ta có\(\left\{ {\begin{array}{*{20}{c}}{SC \bot (AHK)}\\{AI \subset (AHK)}\end{array}} \right. \Rightarrow SC \bot AI\) Do đó C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Đáp án cần chọn là: D
Câu 11:
Cho tam giác đều ABC cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại D lấy điểm S sao cho \(SD = \frac{{a\sqrt 6 }}{2}\). Gọi I là trung điểm BC; kẻ IH vuông góc SA \[(H \in SA).\]Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
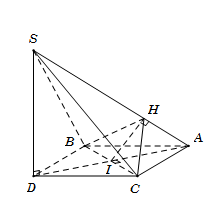
Từ giả thiết suy ra ABDC là hình thoi nên \[BC \bot AD.\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AD}\\{BC \bot SD}\end{array}} \right. \Rightarrow BC \bot (SAD) \Rightarrow BC \bot SA\)
Lại có theo giả thiết\[IH \bot SA\]Từ đó suy ra\[SA \bot \left( {HCB} \right) \Rightarrow SA \bot BH\]
⇒ Đáp án A đúng.
Tính được\[AI = \frac{{a\sqrt 3 }}{2};AD = 2AI = a\sqrt 3 ,S{A^2} = \sqrt {A{D^2} + S{D^2}} = \frac{{3a\sqrt 2 }}{2}.\]
Ta có\[{\rm{\Delta }}AHI \sim {\rm{\Delta }}ADS \Rightarrow \frac{{IH}}{{SD}} = \frac{{AI}}{{AS}} \Rightarrow IH = \frac{{AI.SD}}{{AS}} = \frac{a}{2} = \frac{{BC}}{2} \Rightarrow \]Tam giác HBCHBC có trung tuyến IH bằng nửa cạnh đáy BC nên \[\widehat {BHC} = {90^0}\] hay \[BH \bot HC\]. Do đó D đúng.
Từ mệnh đề A và D suy ra \[BH \bot \left( {SAC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SAC} \right) \Rightarrow \] mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Đáp án cần chọn là: B
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy lớn AB; cạnh bên SA vuông góc với đáy. Gọi Q là điểm trên cạnh SA và \[Q \ne A,\;Q \ne S\]; M là điểm trên đoạn AD và \[M \ne A\]. Mặt phẳng (α) qua QM và vuông góc với mặt phẳng (SAD). Thiết diện tạo bởi \[\left( \alpha \right)\;\]với hình chóp đã cho là:
 Xem đáp án
Xem đáp án
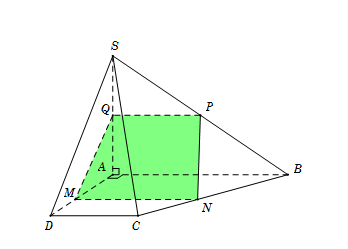
Ta có \(\left\{ {\begin{array}{*{20}{c}}{AB \bot AD}\\{AB \bot SA}\end{array}} \right. \Rightarrow AB \bot (SAD)\)Mà (α)⊥(SAD)(α)⊥(SAD) suy ra AB∥(α)AB∥(α).
Qua M kẻ đường thẳng song song với AB cắt BC tại N.
Qua Q kẻ đường thẳng song song với AB cắt SB tại P.
Khi đó thiết diện là hình thang MNPQ (do \[MN\parallel PQ\]).
Vì \[AB \bot \left( {SAD} \right)\] suy ra \[MN \bot \left( {SAD} \right)\] nên \[MN \bot MQ\]
Do đó thiết diện MNPQ là hình thang vuông tại Q và M.
Đáp án cần chọn là: C
Câu 13:
Cho hình chóp đều S.ABC. Mặt phẳng (α) qua A, song song với BC và vuông góc với mặt phẳng (SBC). Thiết diện tạo bởi (α) với hình chóp đã cho là:
 Xem đáp án
Xem đáp án
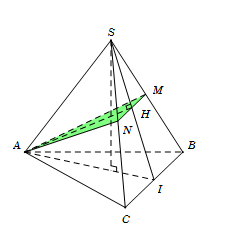
Gọi I là trung điểm BC.
Trong tam giác SAI kẻ \[AH \bot SI\;(H \in SI).\]
Trong tam giác SBC, qua H kẻ đường song song với BC, cắt SC ở MM, cắt SB ở N.
Qua cách dựng ta có \[BC\parallel \left( {AMN} \right).\,\,\left( 1 \right)\]
Và
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{SI \bot AH}\\{SI \bot MN(do\,SI \bot BC)}\end{array}} \right. \Rightarrow SI \bot (AMN)\\ \Rightarrow (SBC) \bot (AMN).\end{array}\)
Từ (1) và (2), suy ra thiết diện cần tìm là tam giác AMN.
Dễ thấy H là trung điểm của MN mà \[AH \bot \left( {SBC} \right)\] suy ra \[AH \bot MN\]. Tam giác AMN có đường cao AH vừa là trung tuyến nên nó là tam giác cân đỉnh A.
Đáp án cần chọn là: B
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB=2a,AD=DC=a; cạnh bên SA=a và vuông góc với đáy. Mặt phẳng (α) qua SD và vuông góc với mặt phẳng (SAC). Tính diện tích S của thiết diện tạo bởi (α) với hình chóp đã cho.
 Xem đáp án
Xem đáp án
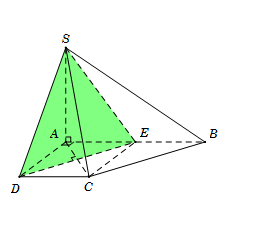
Gọi E là trung điểm AB.
Suy ra AECD là hình vuông nên \[DE \bot AC\]. (1)
Mặt khác\[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot DE\,\,\left( 2 \right)\]
Từ (1) và (2), suy ra\[DE \bot \left( {SAC} \right) \Rightarrow \left( {SDE} \right) \bot \left( {SAC} \right)\]
Ta có\(\left. {\begin{array}{*{20}{c}}{(SDE) \supset SD}\\{(SDE) \bot (SAC)}\end{array}} \right\} \Rightarrow (\alpha ) \equiv (SDE)\)
Vậy thiết diện là tam giác SDE
Ta có\[SD = \sqrt {S{A^2} + D{A^2}} = a\sqrt 2 ;SE = \sqrt {S{A^2} + A{E^2}} = a\sqrt 2 \]
\[DE = AC = DC\sqrt 2 = a\sqrt 2 \]
Do đó tam giác SDE đều có cạnh\[a\sqrt 2 \] nên \[{S_{{\rm{\Delta }}{\kern 1pt} SDE}} = \frac{{S{D^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\]Đáp án cần chọn là: C
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng \({30^0}\). Tính diện tích hình chữ nhật ABCD..
 Xem đáp án
Xem đáp án
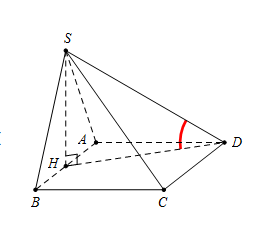
Gọi H là trung điểm của AB, tam giác SAB đều \[ \Rightarrow \,\,SH \bot AB.\]
Mà\[\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)\] và \[SH = \frac{{a\sqrt 3 }}{2}\]Suy ra\[\widehat {(SD;\left( {ABCD} \right))} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH} = {30^0}\]
Tam giác SHD vuông tại H, có\[\tan \widehat {SDH} = \frac{{SH}}{{HD}} \Rightarrow HD = \frac{{3a}}{2}.\]
Tam giác AHD vuông tại A, có\[AD = \sqrt {H{D^2} - A{H^2}} = a\sqrt 2 .\]
Vậy diện tích hình chữ nhật ABCD là\[{S_{ABCD}} = \sqrt 2 \,{a^2}.\]
Đáp án cần chọn là: B
Câu 16:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,AB=a.. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng BC tạo với mặt phẳng (SAC) góc 300. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
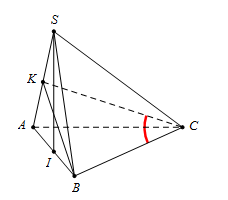
Gọi I là trung điểm của AB, tam giác SAB đều ⇒\(\left\{ {\begin{array}{*{20}{c}}{SI = \frac{{a\sqrt 3 }}{2}}\\{SI \bot AB}\end{array}} \right.\)
Mà \[\left( {SAB} \right) \bot \left( {ABC} \right) \Rightarrow SI \bot \left( {ABC} \right);\left\{ {\begin{array}{*{20}{c}}{SI \bot AC}\\{AB \bot AC}\end{array} \Rightarrow AC \bot (SAB)} \right.\]
Kẻ BK vuông góc với SA tại K, vì \[AC \bot \left( {SAB} \right)\] nên\[AC \bot BK \Rightarrow BK \bot \left( {SAC} \right)\] và\[BK = \frac{{a\sqrt 3 }}{2}\]
Do đó, góc giữa BC và\[mp\,\,\left( {SAC} \right)\] là \[\widehat {BCK}\,\, \Rightarrow \,\,\widehat {BCK} = {30^0}.\]
Khi đó \[BC = \frac{{BK}}{{\sin \widehat {BCK}}} = a\sqrt 3 \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} = a\sqrt 2 .\]
Vậy diện tích tam giác ABC là\[{S_{{\rm{\Delta }}{\kern 1pt} ABC}} = \frac{1}{2}.AB.AC = \frac{{{a^2}\sqrt 2 }}{2}.\]
Đáp án cần chọn là: A
Câu 17:
Trong không gian cho điểm A và mặt phẳng (P). Mệnh đề nào đưới đây đúng ?
 Xem đáp án
Xem đáp án
Có vô số mặt phẳng qua A và vuông góc với (P).
Đáp án cần chọn là: C
Câu 18:
Hình lăng trụ đứng có đáy là hình chữ nhật có bao nhiêu mặt là hình chữ nhật ?
 Xem đáp án
Xem đáp án
Hình lăng trụ đứng có đáy là hình chữ nhật là hình hộp chữ nhật nên có 6 mặt là hình chữ nhật.
Đáp án cần chọn là: C
Câu 19:
Cho hình lăng trụ tam giác đều ABC.A’B’C’, gọi G là trọng tâm tam giác ABC. (tham khảo hình vẽ). Khẳng định nào sau đây là sai?
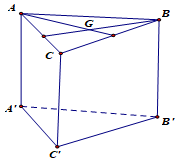
 Xem đáp án
Xem đáp án
Do ABC.A’B’C’ là hình lăng trụ tam giác đều nên \[BB' \bot \left( {ABC} \right)\]
\[ \Rightarrow BB' \bot AG\left( {AG \subset \left( {ABC} \right)} \right)\]Do ABC là tam giác đều nên G vừa là trọng tâm vừa là trực tâm. Do đó:
\(\begin{array}{l}\left. {\begin{array}{*{20}{c}}{AG \bot BC}\\{AG \bot BB\prime }\end{array}} \right\} \Rightarrow AG \bot (BCC\prime B\prime )\\ \Rightarrow AG \bot B\prime C\prime \end{array}\)
\[AA' \bot (ABC)\] vì \[ABC \cdot A'B'C'\] là hình lăng trụ đứng.
Đáp án cần chọn là: D
