Điều kiện xác định:\[\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 > 0}\\{y - 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 1 \vee x < - 1}\\{y > 1}\end{array}} \right.\]</>

Đáp án cần chọn là: B

Ta có:

\(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 1}\\{{4^{x + {y^2}}} = 16}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + 2y = - 1}\\{x + {y^2} = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 2y - 1}\\{{y^2} - 2y - 3 = 0}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 2y - 1}\\{y = - 1;y = 3}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1;y = - 1}\\{x = - 7;y = 3}\end{array}} \right.\)

Vậy hệ đã cho có 2 nghiệm phân biệt.

Đáp án cần chọn là: C

Điều kiện\[x > 0;y > 0\]

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{logx - logy = 2}\\{x - 10y = 900}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{log\frac{x}{y} = 2}\\{x - 10y = 900}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{x}{y} = 100}\\{x - 10y = 900}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 100y}\\{x - 10y = 900}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 100y}\\{100y - 10y = 900}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1000}\\{y = 10}\end{array}} \right.\end{array}\)

Vậy \[A = x - 2y = 1000 - 2.10 = 980\]

Đáp án cần chọn là: A

Nhân vế với vế của hai phương trình ta được:

\[\left( {{2^x}{{.9}^y}} \right).\left( {{3^x}{{.4}^y}} \right) = 162.48 \Leftrightarrow {6^x}{.36^y} = 162.48 \Leftrightarrow {6^x}{.6^{2y}} = {6^5} \Leftrightarrow x + 2y = 5\]

Khi đó

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{x + 2y = 5}\\{{3^x}{{.4}^y} = 48}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5 - 2y}\\{{3^{5 - 2y}}{4^y} = 48}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5 - 2y}\\{\frac{{{3^5}}}{{{9^y}}}{{.4}^y} = {2^4}.3}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5 - 2y}\\{{{\left( {\frac{2}{3}} \right)}^{2y}} = {{\left( {\frac{2}{3}} \right)}^4}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 2}\\{x = 1}\end{array}} \right.\end{array}\)

Vậy hệ có nghiệm duy nhất (1;2).

Đáp án cần chọn là: B

Điều kiện:\(\left\{ {\begin{array}{*{20}{c}}{0 < x \ne 1;0 < x + 1 \ne 1}\\{y > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < x \ne 1}\\{y > 0}\end{array}} \right.\)</></>

Khi đó hệ

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = {x^2}}\\{y + 23 = {{(x + 1)}^3}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = {x^2}}\\{{x^2} + 23 = {{(x + 1)}^3}}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = {x^2}}\\{(x - 2)({x^2} + 4x + 11) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2 = {x_0}}\\{y = 4 = {y_0}}\end{array}} \right.\end{array}\)

Do đó \[{x_0} < {y_0}\]

Đáp án cần chọn là: C

Đặt\(\left\{ {\begin{array}{*{20}{c}}{{6^x} = a > 0}\\{{3^y} = b > 0}\end{array}} \right.\)thì hệ trở thành:

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{a - 2b = 2}\\{ab = 12}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2b + 2}\\{{b^2} + b - 6 = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2b + 2}\\{b = 2(TM);b = - 3(L)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 6}\\{b = 2}\end{array}} \right.\end{array}\)

Do đó \(\left\{ {\begin{array}{*{20}{c}}{{6^x} = 6}\\{{3^y} = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 \in Z}\\{y = lo{g_3}2 \in I}\end{array}} \right.\)

Đáp án cần chọn là: A

ĐKXĐ:\[x - y > 0 \Leftrightarrow x > y\] nên A sai.

Xét phương trình thứ nhất của hệ:\[{\left( {\frac{2}{3}} \right)^{2x - y}} + 6{\left( {\frac{2}{3}} \right)^{\frac{{2x - y}}{2}}} - 7 = 0\]

Đặt\[t = {\left( {\frac{2}{3}} \right)^{\frac{{2x - y}}{2}}} > 0\]thì phương trình trở thành \[{t^2} + 6t - 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1(TM)}\\{t = - 7(L)}\end{array}} \right.\]

Suy ra \[{\left( {\frac{2}{3}} \right)^{\frac{{2x - y}}{2}}} = 1 \Leftrightarrow 2x - y = 0\]

Phương trình thứ hai của hệ\[{3^{{{\log }_9}\left( {x - y} \right)}} = 1 \Leftrightarrow {\log _9}\left( {x - y} \right) = 0 \Leftrightarrow x - y = 1\]

Từ đó ta có:\(\left\{ {\begin{array}{*{20}{c}}{2x - y = 0}\\{x - y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 1}\\{y = - 2}\end{array}} \right.\left( {TM} \right)\)

Vậy hệ có nghiệm duy nhất (−1;−2).

Đáp án cần chọn là: C

Trừ vế với vế của phương trình đầu cho phương trình hai ta được:

\[{2^x} - {2^y} + 2x - 2y = y - x \Leftrightarrow {2^x} + 3x = {2^y} + 3y\]

Xét hàm số\[f\left( t \right) = {2^t} + 3t\]có \[f'\left( t \right) = {2^t}\ln 2 + 3 > 0,\forall t \in R\]nên hàm số đồng biến trên RR.

Do đó \[f\left( x \right) = f\left( y \right) \Leftrightarrow x = y \Rightarrow {2^x} + 2x = 3 + y \Leftrightarrow {2^x} + x = 3\]

Xét hàm\[g\left( x \right) = {2^x} + x\]có \[g'\left( x \right) = {2^x}\ln 2 + 1 > 0,\forall x \in R\]nên hàm số\[y = g\left( x \right)\]đồng biến trên R.

Dễ thấy\[g\left( 1 \right) = 3\] nên x=1 là nghiệm duy nhất của phương trình hay (1;1) là nghiệm duy nhất của hệ.

Vậy \[{x_0} = {y_0} = 1 > 0\]

Đáp án cần chọn là: A

Phương trình\[{3^x} - {3^y} = y - x \Leftrightarrow {3^x} + x = {3^y} + y\]

Xét hàm\[f\left( t \right) = {3^t} + t\]có\[f'\left( t \right) = {3^t}\ln 3 + 1 > 0,\forall t \in R\]nên hàm số đồng biến trên R.

Do đó \[f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\]

Thay y=x vào phương trình\[{x^2} + xy + {y^2} = 12\]ta được:

\[{x^2} + {x^2} + {x^2} = 12 \Leftrightarrow 3{x^2} = 12 \Leftrightarrow x = \pm 2 \Rightarrow y = \pm 2\]

Vậy hệ có nghiệm (2;2),(−2;−2).

Đáp án cần chọn là: C

Trừ phương trình 1 cho 2 vế với vế ta được:

\[{2^x} - {2^y} = 2y - 2x \Leftrightarrow {2^x} + 2x = {2^y} + 2y\]

Xét hàm\[f\left( t \right) = {2^t} + 2t\]có\[f'\left( t \right) = {2^t}\ln 2 + 2 > 0,\forall t \in R\]nên hàm số f(t) đồng biến trên R.

Do đó \[f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\]

Thay y=x vào phương trình\[{2^x} = 2y\]ta được\[{2^x} = 2x \Leftrightarrow {2^x} - 2x = 0\]

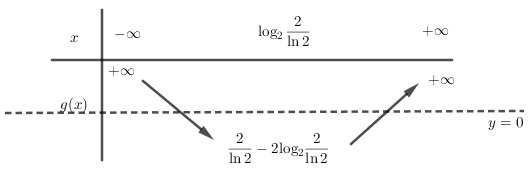
Xét hàm\[y = g\left( x \right) = {2^x} - 2x\]có \[g'\left( x \right) = {2^x}\ln 2 - 2 = 0 \Leftrightarrow x = {\log _2}\frac{2}{{\ln 2}}\]

Suy ra\[g'\left( x \right) > 0 \Leftrightarrow x > {\log _2}\frac{2}{{\ln 2}};g'\left( x \right) < 0 \Leftrightarrow x < {\log _2}\frac{2}{{\ln 2}}\]

\[ \Rightarrow x = {\log _2}\frac{2}{{\ln 2}}\]là điểm cực tiểu của hàm số

\[ \Rightarrow {y_{CT}} = {2^{{{\log }_2}\frac{2}{{\ln 2}}}} - 2{\log _2}\frac{2}{{\ln 2}} = \frac{2}{{\ln 2}} - 2{\log _2}\frac{2}{{\ln 2}} < 0\]

Mặt khác\[\mathop {\lim }\limits_{x \to \pm \infty } g(x) = + \infty \]suy ra đường thẳng y=0 cắt đồ thị hàm số y=g(x) tại 2 điểm phân biệt.

Vậy số nghiệm của hệ là 2

Đáp án cần chọn là: A

Ta thấy: nếu \[\left( {{x_0};{y_0}} \right)\]là nghiệm của hệ thì\[\left( { - {x_0};{y_0}} \right)\]cũng là nghiệm của hệ, do đó\[\left( {0;{y_0}} \right)\]cũng là nghiệm của hệ.

Với x=0 thì \(\left\{ {\begin{array}{*{20}{c}}{1 - {2^y} = y}\\{y = {m^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = {m^2}}\\{{2^y} + y = 1}\end{array}} \right.\)

Xét hàm \[f\left( t \right) = {2^t} + t\]có\[f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\forall t \in R\]nên phương trình\[{2^y} + y = 1\]có nghiệm duy nhất\[y = 0 \Rightarrow {m^2} = 0 \Leftrightarrow m = 0\]

Với m=0 thì hệ trở thành\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{{2^{|x|}} - {2^y} = y - |x|}\\{{x^2} + y = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{2^{|x|}} + |x| = {2^y} + y}\\{{x^2} + y = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{|x| = y}\\{{y^2} + y = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 0}\\{x = 0}\end{array}} \right.\end{array}\)

Do đó hệ có nghiệm duy nhất\[\left( {x;y} \right) = \left( {0;0} \right)\]nếu m=0.

Đáp án cần chọn là: A