Khoảng cách từ điểm đến mặt phẳng
-
489 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \(AB = a\sqrt 2 \). Cạnh bên SA=2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách dd từ D đến mặt phẳng (SBC).
 Xem đáp án
Xem đáp án
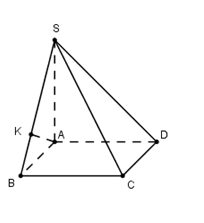
Do AD // BC nên \[d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right).\]
Gọi K là hình chiếu của A trên SB, suy ra\[AK \bot SB\,\,\,\left( 1 \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AK(2)\)
Từ (1) và (2) \[ \Rightarrow AK \bot \left( {SBC} \right)\]
Khi\[d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{2a\sqrt 3 }}{3}.\]
Đáp án cần chọn là: C
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc \({60^ \circ }\)Tính khoảng cách d từ điểm D đến mặt phẳng (SBC).
 Xem đáp án
Xem đáp án
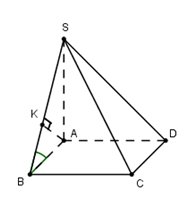
Xác định
\[{60^0} = \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} \Rightarrow SA = AB.\tan \widehat {SBA} = a\sqrt 3 \]
Ta có\[AD\parallel BC \Rightarrow AD\parallel \left( {SBC} \right) \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\]
Kẻ\[AK \bot SB\,\,\,\,\left( 1 \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AK(2)\)
Từ (1) và (2)\[ \Rightarrow AK \bot \left( {SBC} \right)\]
Khi đó\[d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt 3 }}{2}.\]
Vậy\[d\left( {D;\left( {SBC} \right)} \right) = AK = \frac{{a\sqrt 3 }}{2}.\]
Đáp án cần chọn là: A
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \(SA = \frac{{a\sqrt {15} }}{2}\) và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC).
 Xem đáp án
Xem đáp án
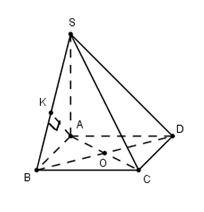
Ta có : \[OA \cap \left( {SBC} \right) = C \Rightarrow \frac{{d\left( {O;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \frac{{OC}}{{AC}} = \frac{1}{2}\]
Do đó\[d\left( {O;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBC} \right)} \right).\]
Gọi K là hình chiếu của A trên\[SB \Rightarrow AK \bot SB\,\,\,\left( 1 \right)\]
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AK(2)\)
Từ (1) và (2)\[ \Rightarrow AK \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AK\]
Tam giác vuông SAB, có\[AK = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt {285} }}{{19}}.\]
Vậy\[d\left( {O;\left( {SBC} \right)} \right) = \frac{1}{2}AK = \frac{{a\sqrt {285} }}{{38}}.\]
Đáp án cần chọn là: C
Câu 4:
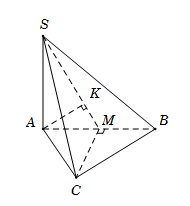
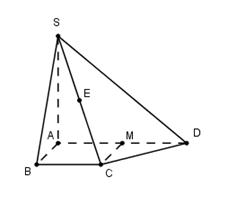
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng \({60^ \circ }\). Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
 Xem đáp án
Xem đáp án
\[\begin{array}{l}{60^0} = \widehat {\left( {SB;\left( {ABC} \right)} \right)}\\ = \widehat {\left( {SB;AB} \right)} = \widehat {SBA};\\SA = AB.\tan \widehat {SBA} = a.\sqrt 3 = a\sqrt 3 .\end{array}\]
Do M là trung điểm của cạnh AB nên \[d\left( {B;\left( {SMC} \right)} \right) = d\left( {A;\left( {SMC} \right)} \right)\]
Trong (SAB) kẻ \[AK \bot SM\,\,\,\left( 1 \right)\]
Ta có : \(\left\{ {\begin{array}{*{20}{c}}{CM \bot AB}\\{CM \bot SA}\end{array}} \right. \Rightarrow CM \bot (SAB) \Rightarrow CM \bot AK(2)\)
Từ (1) và (2)\[ \Rightarrow AK \bot \left( {SCM} \right) \Rightarrow d\left( {A;\left( {SMC} \right)} \right) = AK.\]
Tam giác vuông SAM, có\[AK = \frac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{a\sqrt {39} }}{{13}}\]
Vậy\[d\left( {B;\left( {SMC} \right)} \right) = AK = \frac{{a\sqrt {39} }}{{13}}\]
Đáp án cần chọn là: B
Câu 5:
Cho hình lập phương ABCD,A′B′C′D′ có cạnh bằng 3a. Khoảng cách từ A′ đến mặt phẳng (ABCD) bằng
 Xem đáp án
Xem đáp án
Ta có\[A'A \bot \left( {ABCD} \right) \Rightarrow d\left( {A',\left( {ABCD} \right)} \right) = A'A = 3a\]
Đáp án cần chọn là: D
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh aa. Cạnh bên \(SA = a\sqrt 3 \) và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC).
 Xem đáp án
Xem đáp án
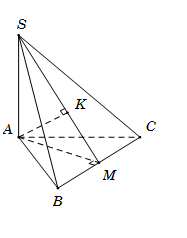
Gọi M là trung điểm BC, suy ra\[AM \bot BC\] và\[AM = \frac{{a\sqrt 3 }}{2}\]
Gọi K là hình chiếu của A trên SM, suy ra \[AK \bot SM\,\,\,\,\,\left( 1 \right)\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{AM \bot BC}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAM) \Rightarrow BC \bot AK\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \[AK \bot \left( {SBC} \right)\] nên\[d\left( {A;\left( {SBC} \right)} \right) = AK.\]
Trong\[{\rm{\Delta }}\,SAM\] có \[AK = \frac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{3a}}{{\sqrt {15} }} = \frac{{a\sqrt {15} }}{5}.\]
Vậy \[d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{a\sqrt {15} }}{5}.\]
Đáp án cần chọn là: A
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên của hình chóp bằng nhau và bằng 2a. Tính khoảng cách d từ A đến mặt phẳng (SCD)
 Xem đáp án
Xem đáp án
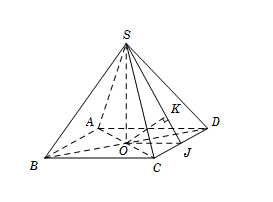
Gọi O là tâm của đáy, suy ra \[SO \bot \left( {ABCD} \right)\]
Ta có
\[\begin{array}{*{20}{l}}{AO \cap \left( {SCD} \right) = C \Rightarrow \frac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \frac{{AC}}{{OC}} = 2}\\{ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right).}\end{array}\]
Gọi J là trung điểm CD, suy ra \[OJ \bot CD\]
Gọi K là hình chiếu của O trên SJ, suy ra\[OK \bot SJ\,\,\,\left( 1 \right)\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{CD \bot OJ}\\{CD \bot SO}\end{array}} \right. \Rightarrow CD \bot (SOJ) \Rightarrow CD \bot OK(2)\)
Từ (1) và (2) \[ \Rightarrow OK \bot \left( {SCD} \right) \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }}\]
Ta có :\[SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {4{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt {14} }}{2} \Rightarrow OK = \frac{{\frac{{a\sqrt {14} }}{2}.\frac{a}{2}}}{{\sqrt {{{\left( {\frac{{a\sqrt {14} }}{2}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} }} = \frac{{a\sqrt 7 }}{{\sqrt {30} }}\]
Vậy\[d\left( {A;\left( {SCD} \right)} \right) = 2.OK = \frac{{2a\sqrt 7 }}{{\sqrt {30} }}.\]
Đáp án cần chọn là: B
Câu 8:
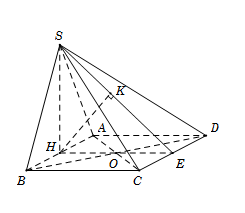
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách d từ A đến (SCD).
 Xem đáp án
Xem đáp án
Gọi H là trung điểm AB, suy ra\[SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right).\]
Gọi E là trung điểm CD; K là hình chiếu vuông góc của H trên SE.
Ta có : \[HE \bot CD,SH \bot CD \Rightarrow CD \bot \left( {SHE} \right) \Rightarrow CD \bot HK\] mà \[HK \bot SE\] nên\[HK \bot \left( {SCD} \right)\]
Do AH//CD nên\(\)\[d\left( {A;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right).\]
Khi đó \[d\left( {H;\left( {SCD} \right)} \right) = HK = \frac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{\sqrt 3 }}{{\sqrt 7 }}.\]
Vậy\[d\left( {A;\left( {SCD} \right)} \right) = HK = \frac{{\sqrt {21} }}{7}.\]
Đáp án cần chọn là: D
Câu 9:
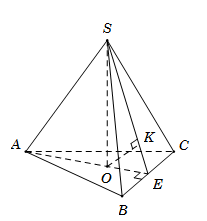
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng \(\frac{{a\sqrt {21} }}{6}\). Tính khoảng cách d từ đỉnh A đến mặt phẳng (SBC) .
 Xem đáp án
Xem đáp án
Gọi O là tâm của tam giác đều ABC.
Do hình chóp S.ABC đều nên suy ra \[SO \bot \left( {ABC} \right)\]
Gọi E là trung điểm BC ta có:
\[\begin{array}{*{20}{l}}{AO \cap \left( {SBC} \right) = E \Rightarrow \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {O;\left( {SBC} \right)} \right)}} = \frac{{AE}}{{OE}} = 3}\\{ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 3.d\left( {O;\left( {SBC} \right)} \right).}\end{array}\]
Trong (SAE) kẻ \[OK \bot SE\,\,\,\,\left( 1 \right)\]
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{BC \bot AE}\\{BC \bot SO}\end{array}} \right. \Rightarrow BC \bot (SAE) \Rightarrow BC \bot OK(2)\)
Từ (1) và (2) \[ \Rightarrow OK \bot \left( {SBC} \right) \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OK\]
Tính được \[SO = \sqrt {S{A^2} - {{\left( {\frac{2}{3}AE} \right)}^2}} = \sqrt {\frac{{21{a^2}}}{{36}} - {{\left( {\frac{2}{3}.\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}\] và\[OE = \frac{1}{3}AE = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}.\]
Tam giác vuông SOE, có\[OK = \frac{{SO.OE}}{{\sqrt {S{O^2} + O{E^2}} }} = \frac{a}{4}\]
Vậy\[d\left( {A;\left( {SBC} \right)} \right) = 3OK = \frac{{3a}}{4}\]
Đáp án cần chọn là: B
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, \[AD = 2BC,\;AB = BC = a\sqrt 3 \]. Đường thẳng SA vuông góc với mặt phẳng (ABCD). Gọi E là trung điểm của cạnh SC. Tính khoảng cách d từ điểm E đến mặt phẳng (SAD).
 Xem đáp án
Xem đáp án
Ta có
\[\begin{array}{*{20}{l}}{EC \cap \left( {SAD} \right) = S \Rightarrow \frac{{d\left( {E;\left( {SAD} \right)} \right)}}{{d\left( {C;\left( {SAD} \right)} \right)}} = \frac{{ES}}{{CS}} = \frac{1}{2}}\\{ \Rightarrow d\left( {E;\left( {SAD} \right)} \right) = \frac{1}{2}d\left( {C;\left( {SAD} \right)} \right)}\end{array}\]
Gọi M là trung điểm AM, suy ra ABCM là hình vuông \[ \Rightarrow CM \bot AD\]
Do
\(\left\{ {\begin{array}{*{20}{c}}{CM \bot AD}\\{CM \bot SA}\end{array}} \right. \Rightarrow CM \bot (SAD) \Rightarrow d(C;(SAD)) = CM = AB = a\sqrt 3 \)
Vậy\[d\left( {E;\left( {SAD} \right)} \right) = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{2}.\]
Đáp án cần chọn là: C
Câu 11:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc 300. Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a.
 Xem đáp án
Xem đáp án
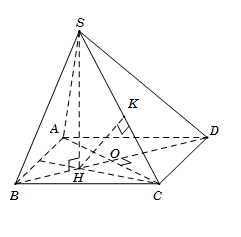
Tam giác ABC đều cạnh aa, H là trọng tâm tam giác nên \[BH = \frac{2}{3}BO = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow HD = BD - BH = a\sqrt 3 - \frac{{a\sqrt 3 }}{3} = \frac{{2a\sqrt 3 }}{3}\]
Xác định\[{30^0} = \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH}\] và\[SH = HD.\tan \widehat {SDH} = \frac{{2a\sqrt 3 }}{3}.\frac{1}{{\sqrt 3 }} = \frac{{2a}}{3}\]
Ta có:
\[\begin{array}{*{20}{l}}{BH \cap \left( {SCD} \right) = D \Rightarrow \frac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \frac{{BD}}{{HD}} = \frac{3}{2}}\\{ \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \frac{3}{2}.d\left( {H;\left( {SCD} \right)} \right)}\end{array}\]
Ta có\[HC \bot AB \Rightarrow HC \bot CD\]
Kẻ\[HK \bot SC\,\,\,\,\left( 1 \right)\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{CD \bot HC}\\{CD \bot SH}\end{array}} \right. \Rightarrow CD \bot (SHC) \Rightarrow CD \bot HK(2)\)
Từ (1) và (2)\[ \Rightarrow HK \bot \left( {SCD} \right) \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\]
Tam giác vuông SHC, có
\[HK = \frac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }} = \frac{{\frac{{2a}}{3}.\frac{{a\sqrt 3 }}{3}}}{{\sqrt {{{\left( {\frac{{2a}}{3}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} }} = \frac{{2a\sqrt {21} }}{{21}}\]
Vậy\[d\left( {B;\left( {SCD} \right)} \right) = \frac{3}{2}HK = \frac{{a\sqrt {21} }}{7}\]
Đáp án cần chọn là: B
Câu 12:
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với đáy, SA=AB=a và AD=x.a. Gọi E là trung điểm của SC. Tìm x, biết khoảng cách từ điểm E đến mặt phẳng (SBD) bằng \(h = \frac{a}{3}\).
 Xem đáp án
Xem đáp án
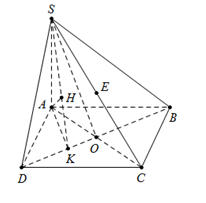
Ta có\[E \in SC\]
\[EC \cap \left( {SBD} \right) = S \Rightarrow \frac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \frac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \frac{{ES}}{{CS}} = \frac{1}{2}\]
Từ A kẻ\[AK \bot BD\left( {K \in BD} \right)\] kẻ\[AH \bot SK\,\,\left( {H \in SK} \right)\,\,\,\,\,\,\left( 1 \right)\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{BD \bot AK}\\{BD \bot SA}\end{array}} \right. \Rightarrow BD \bot (SAK) \Rightarrow BD \bot AH(2)\)
Từ (1) và (2)\[ \Rightarrow AH \bot \left( {SBD} \right).\]
\[ \Rightarrow AH = d\left( {A;\left( {SBD} \right)} \right) = 2.d\left( {E;\left( {SBD} \right)} \right) = \frac{{2a}}{3}.\]
Mà \[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} \Rightarrow AK = \frac{{SA.AH}}{{\sqrt {S{A^2} - A{H^2}} }} = \frac{{2a}}{{\sqrt 5 }}\]
Tam giác ABD vuông tại A, có đường cao AK.
\( \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{A{K^2}}} \Leftrightarrow \frac{1}{{{a^2}}} + \frac{1}{{{a^2}{x^2}}} = \frac{5}{{4{a^2}}}\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 0}\\{{x^2} = 4}\end{array}} \right. \Rightarrow x = 2\)
Đáp án cần chọn là: C
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, AD=2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm SD, hãy tính theo aa khoảng cách dd từ M đến mặt phẳng (SAC).
 Xem đáp án
Xem đáp án
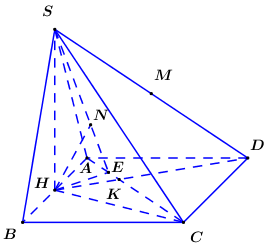
Bước 1: Đổi \[d\left( {M;\left( {SAC} \right)} \right)\] sang \[d\left( {H;\left( {SAC} \right)} \right)\]
Gọi H là trung điểm AB. Vì \[\Delta SAB\] cân tại S nên\[SH \bot AB\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \cap (ABCD) = AB}\\{SH \subset (ABCD),SH \bot AB}\end{array}} \right. \Rightarrow SH \bot \left( {ABCD} \right)\)
Gọi \[K = HD \cap AC\] Áp dụng định lí Ta-let ta có\[\frac{{DK}}{{HK}} = \frac{{DC}}{{AH}} = 2 \Rightarrow DK = 2HK\]
Ta có \[MD \cap \left( {SAC} \right) = S \Rightarrow \frac{{d\left( {M;\left( {SAC} \right)} \right)}}{{d\left( {D;\left( {SAC} \right)} \right)}} = \frac{{SM}}{{SD}} = \frac{1}{2}\]
\[ \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \frac{1}{2}d\left( {D;\left( {SAC} \right)} \right)\]
Lại có\[DH \cap \left( {SAC} \right) = K\] nên\[\frac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \frac{{DK}}{{HK}} = 2 \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\]
Bước 2: Trong (ABCD) kẻ \[HE \bot AC\,\,\left( {E \in AC} \right)\] trong (SHE) kẻ\[HN \bot SE\,\,\left( {N \in SE} \right)\] chứng minh\[HN \bot \left( {SAC} \right)\]
Do đó\[d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right)\]
Trong (ABCD) kẻ\[HE \bot AC\,\,\left( {E \in AC} \right)\], trong (SHE) kẻ\[HN \bot SE\,\,\left( {N \in SE} \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{AC \bot HE}\\{AC \bot SH}\end{array}} \right. \Rightarrow AC \bot (SHE) \Rightarrow AC \bot HN\left\{ {\begin{array}{*{20}{c}}{HN \bot SE}\\{HN \bot AC}\end{array} \Rightarrow HN \bot (SAC)} \right.\)
\[ \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HN\]
Bước 3: Xác định góc giữa SC và (ABCD), từ đó tính SH.
Vì \[SH \bot \left( {ABCD} \right)\] nên HC là hình chiếu vuông góc của SC lên (ABCD)
\[ \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}\]
\[ \Rightarrow {\rm{\Delta }}SHC\] vuông cân tại \[H \Rightarrow SH = HC = \sqrt {B{C^2} + B{H^2}} \]
\[ = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {17} }}{2}\]
Bước 4: Tính\[d\left( {M;\left( {SAC} \right)} \right)\]
Ta có: \[{S_{HAC}} = \frac{1}{2}HE.AC = \frac{1}{2}{S_{ABC}}\]
\[ \Rightarrow HE.AC = \frac{1}{2}.AB.BC\]
\[ \Rightarrow HE = \frac{{\frac{1}{2}.AB.BC}}{{AC}} = \frac{{\frac{1}{2}.a.2a}}{{\sqrt {{a^2} + {{\left( {2a} \right)}^2}} }} = \frac{a}{{\sqrt 5 }}\]
Áp dụng hệ thức lượng trong tam giác vuông SHE ta có:
Nên\[HN = \frac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{\frac{{a\sqrt {17} }}{2}.\frac{a}{{\sqrt 5 }}}}{{\sqrt {\frac{{17{a^2}}}{4} + \frac{{{a^2}}}{5}} }} = \frac{{a\sqrt {1513} }}{{89}}\]
Vậy \[d\left( {M;\left( {SAC} \right)} \right) = \frac{{a\sqrt {1513} }}{{89}}\]
Câu 14:
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có độ dài cạnh đáy AB=8,, cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi M là trung điểm của cạnh A′C′. Khoảng cách từ B′ đến mặt phẳng (ABM) bằng bao nhiêu?
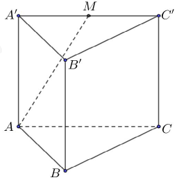
 Xem đáp án
Xem đáp án
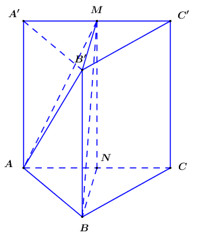
Bước 1: Gọi N là trung điểm của AC, chứng minh\[d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right) = AN\]
Gọi N là trung điểm của AC ta có\[\left( {BB'M} \right) \equiv \left( {BB'MN} \right)\] nên\[d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right)\]
Vì tam giác ABC đều nên\[AN \bot BN\] Ta có\(\left\{ {\begin{array}{*{20}{c}}{AN \bot BN}\\{AN \bot MN}\end{array}} \right. \Rightarrow AN \bot (BB\prime MN)\) nên\[d\left( {A;\left( {BB'MN} \right)} \right) = AN = 4\]
Bước 2: Tính\[{V_{A.BB'M}} = \frac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{{\rm{\Delta }}BB'M}} = {V_{B'.ABM}}\]
Ta lại có\[BN = \frac{{AB\sqrt 3 }}{2} = 4\sqrt 3 ,\,\,MN = AA' = \sqrt 6 \] nên
\[{S_{BB'MN}} = MN.BN = \sqrt 6 .4\sqrt 3 = 12\sqrt 2 \Rightarrow {S_{{\rm{\Delta }}BB'M}} = 6\sqrt 2 \]
\[ \Rightarrow {V_{A.BB'M}} = \frac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{{\rm{\Delta }}BB'M}} = \frac{1}{3}.4.12\sqrt 2 = 16\sqrt 2 = {V_{B'.ABM}}\]
Bước 3: Sử dụng\[d\left( {B';\left( {ABM} \right)} \right) = \frac{{3{V_{B'.ABM}}}}{{{S_{{\rm{\Delta }}ABM}}}}\]
Lại có\[{V_{B'.ABM}} = \frac{1}{3}d\left( {B';\left( {ABM} \right)} \right).{S_{{\rm{\Delta }}ABM}}\] nên\[d\left( {B';\left( {ABM} \right)} \right) = \frac{{3{V_{B'.ABM}}}}{{{S_{{\rm{\Delta }}ABM}}}}\]
Ta có:
\[\begin{array}{*{20}{l}}{AM = \sqrt {A'{A^2} + A'{M^2}} }\\{ = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {4^2}} = \sqrt {22} }\\{AB = 8}\\{BM = \sqrt {B{B^{\prime 2}} + B'{M^2}} }\\{ = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 3\sqrt 6 }\end{array}\]
Bước 4: Sử dụng công thức\[{S_{{\rm{\Delta }}ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \] với p là nửa chu vi tam giác ABM.
Gọi p là nửa chu vi tam giác ABM ta có\[p = \frac{{\sqrt {22} + 8 + 3\sqrt 6 }}{2}\]
\[ \Rightarrow {S_{{\rm{\Delta }}ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} = 12\sqrt 2 \]
Vậy\[d\left( {B';\left( {ABM} \right)} \right) = \frac{{3{V_{B'.ABM}}}}{{{S_{{\rm{\Delta }}ABM}}}} = \frac{{3.16\sqrt 2 }}{{12\sqrt 2 }} = 4\]
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) một góc \({30^0}\).Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a.
 Xem đáp án
Xem đáp án
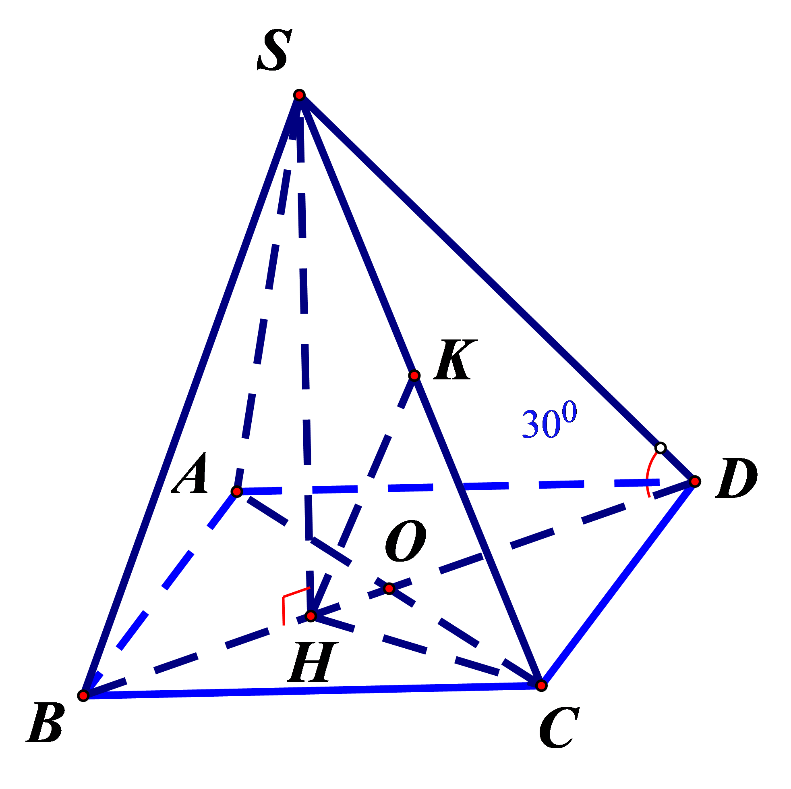
Bước 1: Gọi \[O = AC \cap BD\] Tính BO, CH, HD theo a.
Gọi\[O = AC \cap BD\]
Ta có \[{\rm{\Delta }}ABC\] dều cạnh a có H là trọng tâm
\[ \Rightarrow BO = \frac{{a\sqrt 3 }}{2},CH = \frac{{a\sqrt 3 }}{3},HD = \frac{4}{3}BO = \frac{{2a\sqrt 3 }}{3}\]
Bước 2: Tính SH theo a.
Mặt khác,\[(\widehat {SD,(ABCD)}) = \widehat {SDH} = {30^ \circ }\]
\[ \Rightarrow SH = HD \cdot \tan \widehat {SDH} = \frac{{2a}}{3}\]
Lại có\[CH \bot AB \Rightarrow CH \bot CD\]
Bước 3: Kẻ \[HK \bot SC(K \in SC)\] Chứng minh \[HK \bot CD\]
Kẻ \[HK \bot SC(K \in SC)\]
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{SH \bot CD}\\{CH \bot CD}\end{array} \Rightarrow CD \bot (SHC) \Rightarrow HK \bot CD \Rightarrow HK \bot (SCD)} \right.\)
Bước 4: Tính\[d\left( {B,\left( {SCD} \right)} \right)\]
\[ \Rightarrow d(H,(SCD)) = HK = \frac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }} = \frac{{2a\sqrt {21} }}{{21}}\]
Mà\[\frac{{d(H,(SCD))}}{{d(B,(SCD))}} = \frac{{HD}}{{BD}} = \frac{2}{3} \Rightarrow d(B,(SCD)) = \frac{{a\sqrt {21} }}{7}\]
Đáp án cần chọn là: C
Câu 16:
Cho tứ diện OABC có ba cạnh OA,OB,OC đôi một vuông góc với nhau. Biết khoảng cách từ điểm O đến các đường thẳng BC,CA,AB lần lượt là \(a,a\sqrt 2 ,a\sqrt 3 \). Khoảng cách từ điểm O đến mặt phẳng (ABC) là \(\frac{{2a\sqrt m }}{{11}}\). Tìm m.
 Xem đáp án
Xem đáp án
Trả lời:
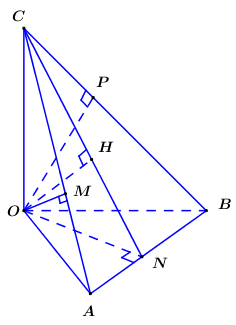
Bước 1: Kẻ \[OM \bot AC\,\,\left( {M \in AC} \right),ON \bot AB\,\,\left( {N \in AB} \right),OP \bot BC\,\,\left( {P \in BC} \right)\]
Kẻ\[OM \bot AC\,\,\left( {M \in AC} \right),ON \bot AB\,\,\left( {N \in AB} \right),OP \bot BC\,\,\left( {P \in BC} \right)\]
Khi đó ta có \[OP = a,\,\,OM = a\sqrt 2 ,\,\,ON = a\sqrt 3 \]
Bước 2: Trong (OCN) kẻ \[OH \bot CN\,\,\left( {H \in CN} \right)\] chứng minh\[OH \bot \left( {ABC} \right)\]
Trong (OCN) kẻ\[OH \bot CN\,\,\left( {H \in CN} \right)\] ta có:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{AB \bot ON}\\{AB \bot OC}\end{array}} \right. \Rightarrow AB \bot (OCN) \Rightarrow AB \bot OH\\\left\{ {\begin{array}{*{20}{c}}{OH \bot AB}\\{OH \bot CN}\end{array}} \right. \Rightarrow OH \bot (ABC) \Rightarrow d(O;(ABC)) = OH\end{array}\)
Bước 3: Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\[\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\]
Lại có
\[\frac{1}{{O{M^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{C^2}}};\frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}};\frac{1}{{O{P^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\]
\[\begin{array}{l} \Rightarrow \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}} = 2\left( {\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}} \right)\\ \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}}} \right)\\ \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{2{a^2}}} + \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}}} \right) = \frac{{11}}{{12{a^2}}}\\ \Rightarrow \frac{1}{{O{H^2}}} = \frac{{11}}{{12{a^2}}} \Rightarrow OH = \frac{{2a\sqrt {33} }}{{11}}\end{array}\]
\( \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = \frac{{2a\sqrt {33} }}{{11}}\)
Vậy m=33.
