10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 CD Bài tập cuối chương 7 (Vận dụng) có đáp án

Câu 1:

Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là

Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. (ảnh 1)

A. $Δ B A C = Δ D A C$ ;

B. $Δ B A H = Δ H A D$ ;

C. AC ⊥ BD;

D. H là trung điểm của BD.

Xem đáp án

Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. (ảnh 2)

Câu 2:

Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết $\hat{A B D} = 30 °$ . Số đo góc ACB là

A. 150°;

B. 60°;

C. 30°;

D. 90°.

Xem đáp án

Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. (ảnh 1)

Câu 3:

Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là

A. AE;

B. DC;

C. ED;

D. ED và DC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

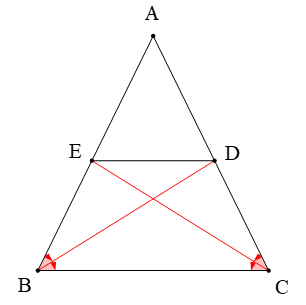
Cho tam giác ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. (ảnh 1)

Ta có ∆ABC cân tại A (giả thiết) suy ra $\hat{A B C} = \hat{A C B}$ (tính chất)

BD là tia phân giác góc B nên $\hat{E B D} = \hat{D B C} = \frac{1}{2} \hat{A B C}$

CE là tia phân giác góc C nên $\hat{D C E} = \hat{E C B} = \frac{1}{2} \hat{A C B}$

Do đó $\hat{E B D} = \hat{D B C} = \hat{D C E} = \hat{E C B}$

Xét ∆BEC và ∆CDB có:

$\hat{A B C} = \hat{A C B}$

BC là cạnh chung

$\hat{E C B} = \hat{D B C}$ (chứng minh trên)

Suy ra ∆BEC = ∆CDB (g.c.g)

Do đó BE = CD (hai cạnh tương ứng)

Mà BE + EA = AB; CD + DA = AC

AB = AC (tam giác ABC cân tại A)

Suy ra EA = DA ⇒ ∆AED cân tại A ⇒ $\hat{A E D} = \hat{A D E}$ (tính chất)

Mà $\hat{A E D} + \hat{A D E} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{A E D} = \frac{180 ° - \hat{B A C}}{2}$ (1)

Có $\hat{A B C} = \hat{A C B}$ mà $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{A B C} = \frac{180 ° - \hat{B A C}}{2}$ (1)

Từ (1) và (2) suy ra $\hat{A E D} = \hat{A B C}$ mà hai góc đồng vị nên ED // BC.

Suy ra $\hat{E D B} = \hat{D B C}$ (hai góc so le trong)

Mà $\hat{E D B} = \hat{D B C}$ (chứng ninh trên)

Suy ra $\hat{E D B} = \hat{E B D}$

Do đó tam giác EBD cân tại E (dấu hiệu nhận biết)

Suy ra EB = ED

Vậy BE = CD = ED.

Câu 4:

Cho $\hat{x O y}$ khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?

A. ∆OBM = ∆OMA;

B. $\hat{O M B} = \hat{O A M}$ ;

C. ∆OBM = ∆OBA;

D. OM là tia phân giác của góc

\hat{x O y}

.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

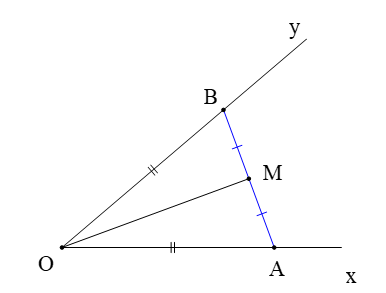
Cho góc xOy khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. (ảnh 1)

M là trung điểm của AB (giả thiết) nên MB = MA

Xét ∆OBM và ∆OMA có

OB = OA (giả thiết)

OM là cạnh chung

MB = MA (chứng minh trên)

Suy ra ∆OBM = ∆OAM (c.c.c)

Do đó $\hat{O M B} = \hat{O M A}$ (hai góc tương ứng)

$\hat{B O M} = \hat{A O M}$ (hai góc tương ứng)

Suy ra OM là tia phân giác góc BOA hay góc xOy.

Câu 5:

Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.

A. BD = CE;

B. BE = CD;.

C. BK = KC;

D. DK = KC

Xem đáp án

Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. (ảnh 1)

Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. (ảnh 2)

Câu 6:

Cho ∆ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. So sánh BN với BC + MN đúng là

A. $B N > \frac{B C + M N}{2}$ ;

B. $B N < \frac{B C + M N}{2}$ ;

C. $B N = \frac{B C + M N}{2}$ ;

D. Không đủ dữ kiện để so sánh.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

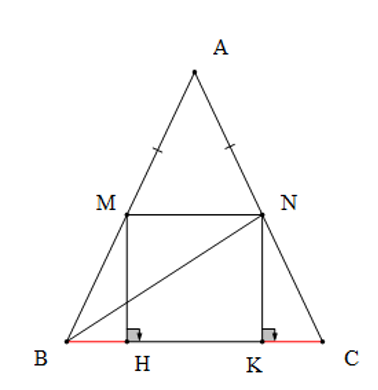
Cho tam giác ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. (ảnh 1)

∆ABC cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B}$ (tính chất)

Mà AM = AN (giả thiết) suy ra BM = CN

Xét hai tam giác vuông MBH và NCK có:

$\hat{A B C} = \hat{A C B}$

BM = CN

Suy ra ∆MBH = ∆NCK (cạnh huyền – góc nhọn)

Do đó: BH = CK và MH = NK

Có AM = AN (giả thiết) suy ra ∆AMN cân tại A

⇒ $\hat{A M N} = \hat{A N M}$ (tính chất)

Mà $\hat{A M N} + \hat{A N M} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{A M N} = \frac{180 ° - \hat{B A C}}{2}$ (1)

Có $\hat{B} = \hat{C}$ mà $\hat{B} + \hat{C} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{B} = \frac{180 ° - \hat{B A C}}{2}$ (1)

Từ (1) và (2) suy ra $\hat{A M N} = \hat{B}$ mà hai góc đồng vị nên MN // BC.

Mà BC ⊥ MH nên MN ⊥ MH

Xét hai tam giác vuông HMN và NKH có

MH = NK (chứng minh trên)

NH là cạnh chung

Suy ra ∆HMN = ∆NKH (cạnh huyền – cạnh góc vuông)

Do đó MN = HK

Mặt khác: BN > BK (quan hệ đường vuông góc – đường xiên)

Suy ra: 2BN > 2BK = 2(BH + HK) = 2BH + 2HK = BH + KC + MN + HK = BC + MN

Do đó: $B N > \frac{B C + M N}{2}$ .

Câu 7:

Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là

A. Chu vi ∆AFB nhỏ hơn chu vi ∆AMB;

B. Chu vi ∆AFB lớn hơn chu vi ∆AMB;

C. Chu vi ∆AFB bằng chu vi ∆AMB;

D. Không đủ dữ kiện để so sánh.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

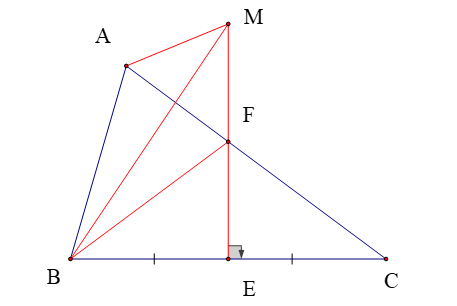
Cho tam giác ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại (ảnh 1)

Ta có: FE là đường trung trực của BC (giả thiết)

⇒ FB = FC (tính chất đường trung trực)

M thuộc đường trung trực của BC ⇒ MB = MC (tính chất đường trung trực)

Chu vi ∆AFB = AB + AF + FB = AB + AF + FC = AB + AC

Chu vi ∆AMB = AB + AM + MB = AB + AM + MC

Xét ∆AMC có: AM + MC > AC (bất đẳng thức tam giác)

Do đó: AB + AC < AB + AM + MC

Hay chu vi ∆AFB nhỏ hơn chu vi ∆AMB.

Câu 8:

Cho ∆ABC cân tại A, trên các cạnh AB, AC lần lượt lấy hai điểm P và Q sao cho AP = AQ. Hai đoạn thẳng CP và BQ cắt nhau tại O. OH và OK lần lượt là khoảng cách từ O đến AB và AC. Khẳng định nào dưới đây sai?

A. Tam giác OBC cân;

B. OH ≠ OK;

C. AO là tia phân giác góc A;

D. OP = OQ.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

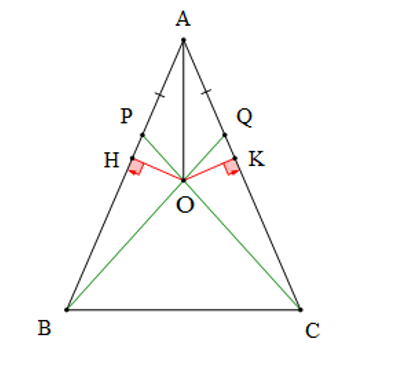
Cho tam giác ABC cân tại A, trên các cạnh AB, AC lần lượt lấy hai điểm P và Q sao cho AP = AQ (ảnh 1)

∆ABC cân tại A nên AB = AC

Xét ∆ABQ và ∆ACP có

AP = AQ (giả thiết)

Góc A chung

AB = AC

Suy ra ∆ABQ = ∆ACP (c.g.c)

Do đó $\hat{A B Q} = \hat{A C P}$ (hai góc tương ứng)

Mà $\hat{A B C} = \hat{A C B}$ (tính chất tam giác cân)

Nên $\hat{O B C} = \hat{O C B}$

Suy ra ∆OBC cân tại O.

⇒ OB = OC

Mà ∆ABQ = ∆ACP nên BQ = PC (hai cạnh tương ứng)

Do đó OP = OQ

Xét ∆APO và ∆AQO có

AO là cạnh chung

OP = OQ (cmt)

AP = AQ (giả thiết)

Suy ra ∆APO = ∆AQO (c.c.c)

Do đó $\hat{P A O} = \hat{Q A O}$ (hai góc tương ứng)

⇒ AO là tia phân giác góc A

⇒ OH = OK (tính chất tia phân giác của một góc)

Vậy B sai.

Câu 9:

Cho ∆ABC có $\hat{A} = 60 °$ . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?

A. Trung trực của EF đi qua A;

B. BE + CF = BC;

C. $\hat{E A F} = 120 °$ ;

D. Cả A, B và C đều sai.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

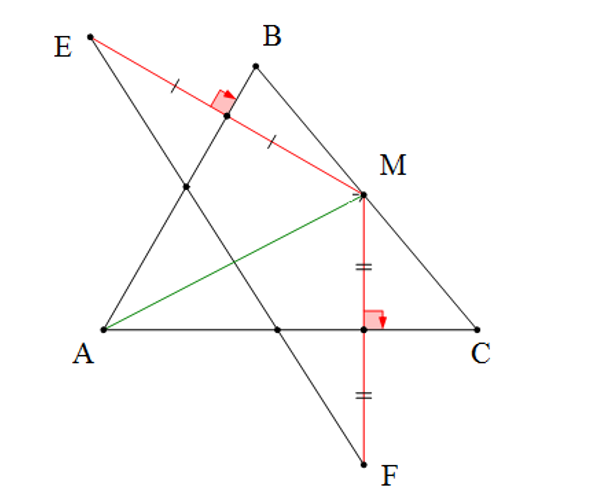
Cho tam giác ABC có góc A= 60 độ. M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB (ảnh 1)

+) Ta có AB là trung trực của ME (giả thiết) ⇒ AE = AM (tính chất đường trung trực)

AC là trung trực của MF (giả thiết) ⇒ AF = AM (tính chất đường trung trực)

Do đó AE = AF ⇒ A thuộc đường trung trực của EF

Hay trung trực của EF đi qua A.

+) Ta có: B thuộc đường trung trực của ME ⇒ BE = BM (tính chất đường trung trực)

C thuộc đường trung trực của MF ⇒ CF = CM (tính chất đường trung trực)

Mà BM + CM = BC

Nên BE + CF = BC

+) Xét ∆AEB và ∆AMB có

AE = AM

AB là cạnh chung

EB = MB

Suy ra ∆AEB = ∆AMB (c.c.c)

⇒ $\hat{E A B} = \hat{M A B}$ (hai góc tương ứng)

Xét ∆AFC và ∆AMC có

AF = AM

AC là cạnh chung

FC = MC

Suy ra ∆AFC = ∆AMC (c.c.c)

⇒ $\hat{F A C} = \hat{M A C}$ (hai góc tương ứng)

Ta có: $\hat{E A F} = \hat{E A B} + \hat{M A B} + \hat{F A C} + \hat{M A C}$

⇒ $\hat{E A F} = 2 \hat{M A B} + 2 \hat{M A C} = 2 (\hat{M A B} + \hat{M A C}) = 2 \hat{B A C} = 2.60 ° = 120 °$ .

Câu 10:

Cho ∆ABC nhọn có đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng nhất.

A. ∆AIK cân tại A;

B. ∆AIK vuông cân tại A;

C. ∆AIK đều;

D. ∆AIK vuông tại A.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

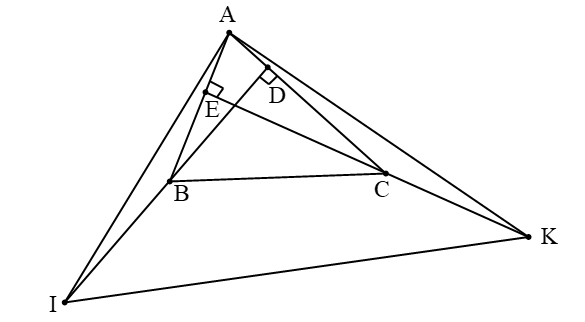
Cho tam giác ABC nhọn có đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho (ảnh 1)

Ta có:

∆BDA vuông tại D ⇒ $\hat{A B D} + \hat{B A C} = 90 °$

∆CEA vuông tại E ⇒ $\hat{A C E} + \hat{B A C} = 90 °$

Do đó $\hat{A B D} = \hat{A C E}$

Mặt khác:

$\hat{A B D} + \hat{A B I} = 180 °$ (hai góc kề bù)

$\hat{A C E} + \hat{A C K} = 180 °$ (hai góc kề bù)

Do đó: $\hat{A B I} = \hat{A C K}$

Xét ∆ABI và ∆KCA có

AB = KC (giả thiết)

$\hat{A B I} = \hat{A C K}$ (chứng minh trên)

BI = AC (giả thiết)

Suy ra ∆ABI = ∆KCA (c.g.c)

Do đó AI = AK (hai cạnh tương ứng) ⇒ ∆AIK cân tại A (1)

Vì ∆ABI = ∆KCA ⇒ $\hat{A I B} = \hat{K A C}$ (hai góc tương ứng)

∆IDA vuông tại D ⇒ $\hat{A I B} + \hat{I A D} = 90 °$

Do đó $\hat{K A C} + \hat{I A D} = 90 °$

Hay $\hat{K A I} = 90 °$ (2)

Từ (1) và (2) suy ra ∆AIK vuông cân tại A.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 7 CD Bài tập cuối chương 7 (Phần 2) có đáp án

Trắc nghiệm Toán 7 CD Bài tập cuối chương 7 (Vận dụng) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương