7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 KNTT Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của 1 góc (Thông hiểu) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của 1 góc (Phần 2) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của 1 góc (Thông hiểu) có đáp án

672 lượt thi
7 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

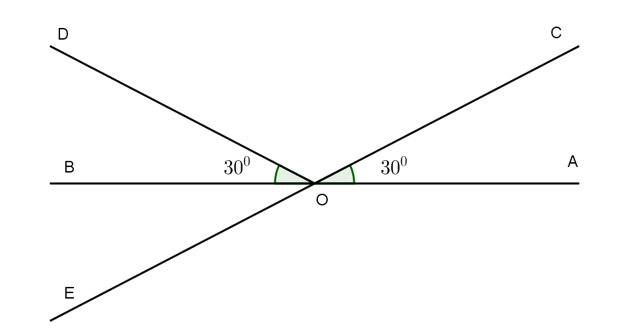
Cho hai đường thẳng AB, CE cắt nhau tại O và tia OD như hình vẽ. Trong các khẳng định sau, khẳng định nào sai?

Cho hai đường thẳng AB, CE cắt nhau tại O và tia OD như hình vẽ. Trong các (ảnh 1)

A. Góc đối đỉnh với $\hat{AOC}$ là $\hat{EOB}$ ;

B. Góc đối đỉnh với $\hat{AOC}$ là $\hat{DOB}$ ;

C. $\hat{EOB}$ = $\hat{DOB}$ ;

\hat{EOB}

\hat{AOC}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Vì hai đường thẳng AB và CE cắt nhau tại O nên OA là tia đối của tia OB , OC là tia đối của tia OE. Suy ra góc đối đỉnh với $\hat{AOC}$ là $\hat{EOB}$ ( định nghĩa) . Khẳng định A đúng.

Khẳng định B sai vì góc đối đỉnh với $\hat{AOC}$ là $\hat{EOB}$ , không phải $\hat{DOB}$ .

Khẳng định D đúng vì $\hat{AOC}$ và $\hat{EOB}$ là hai góc đối đỉnh nên $\hat{EOB}$ = $\hat{AOC}$ (tính chất)

Khẳng định C đúng vì $\hat{EOB}$ = $\hat{AOC}$ = 30° = $\hat{DOB}$ .

Vậy đáp án đúng là B.

Câu 2:

Cho hai đường thẳng AB và CD cắt nhau tại O. $\hat{AOC} = \frac{1}{5} \hat{BOC}$ . Tính $\hat{B O D}$ ?

A. 60°;

B. 30°;

C. 120°;

D. 150°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Suy ra $\hat{BOD}$ và $\hat{AOC} $ là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).

Ta có $\hat{BOD}$ = $\hat{AOC} $ ( Tính chất hai góc đối đỉnh ).

Lại có: $\hat{AOC} = \frac{1}{5} \hat{BOC} \Rightarrow 5. \hat{AOC} = \hat{BOC}$

mà $\hat{AOC} + \hat{BOC} = \hat{AOB} = 180 °$ ⇒ 6 $\hat{AOC} $ = 180° ⇒ $\hat{AOC} $ = 30° = $\hat{BOD}$ .

Vậy $\hat{BOD}$ = 30°. Đáp án đúng là B.

Câu 3:

Cho $\hat{xOy}$ đối đỉnh với $\hat{x'Oy'}$ và $\hat{xOy} = 60 °$ . Tính số đo góc kề bù với $\hat{x'Oy'}$ .

A. 150°;

B. 60°;

C. 120°;

D. 30°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

$\hat{xOy}$ và $\hat{x'Oy'}$ là hai góc đối đỉnh nên $\hat{xOy}$ = $\hat{x'Oy'}$ = 60° ( Tính chất hai góc đối đỉnh ).

Gọi $\hat{O_{1}}$ là góc kề bù với $\hat{x'Oy'}$ . Ta có $\hat{O_{1}}$ + $\hat{x'Oy'}$ = 180° ( Tính chất hai góc kề bù )

⇒ $\hat{O_{1}}$ + 60° = 180°.

⇒ $\hat{O_{1}}$ = 120°.

Vậy đáp án đúng là C.

Cho

\hat{xOy}

đối đỉnh với

\hat{x'Oy'}

và

\hat{xOy} = 60 °

. Tính số đo góc kề bù với

\hat{x'Oy'}

Câu 4:

Cho hai đường thẳng AB và CD cắt nhau tại O sao cho $\hat{BOD}$ = 43°. Khẳng định nào sau đây sai?

A. $\hat{AOC} = 43 °$ ;

B. $\hat{BOC} = 137 °$ ;

C. $\hat{AOD} = 137 °$ ;

\hat{C O A} = 137 °

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Vậy $\hat{BOD}$ và $\hat{AOC} $ là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).

Nên $\hat{BOD}$ = $\hat{AOC} $ = 43°. Khẳng định A đúng. Khẳng định D sai.

Hai góc $\hat{BOD}$ và $\hat{AOD}$ có một cạnh chung OD, hai cạnh OA và OB là hai tia đối nhau nên $\hat{BOD}$ và $\hat{AOD}$ là hai góc kề bù ( Định nghĩa hai góc kề bù ).

Ta có $\hat{BOD}$ + $\hat{AOD}$ = 180° ( Tính chất hai góc kề bù )

⇒ $\hat{AOD}$ = 180° $\hat{BOD}$ = 137°. Khẳng định C đúng.

Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Vậy $\hat{BOC}$ và $\hat{AOD}$ là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).

⇒ $\hat{BOC}$ = $\hat{AOD}$ = 137°. Khẳng định B đúng.

Vậy đáp án đúng là D.

Câu 5:

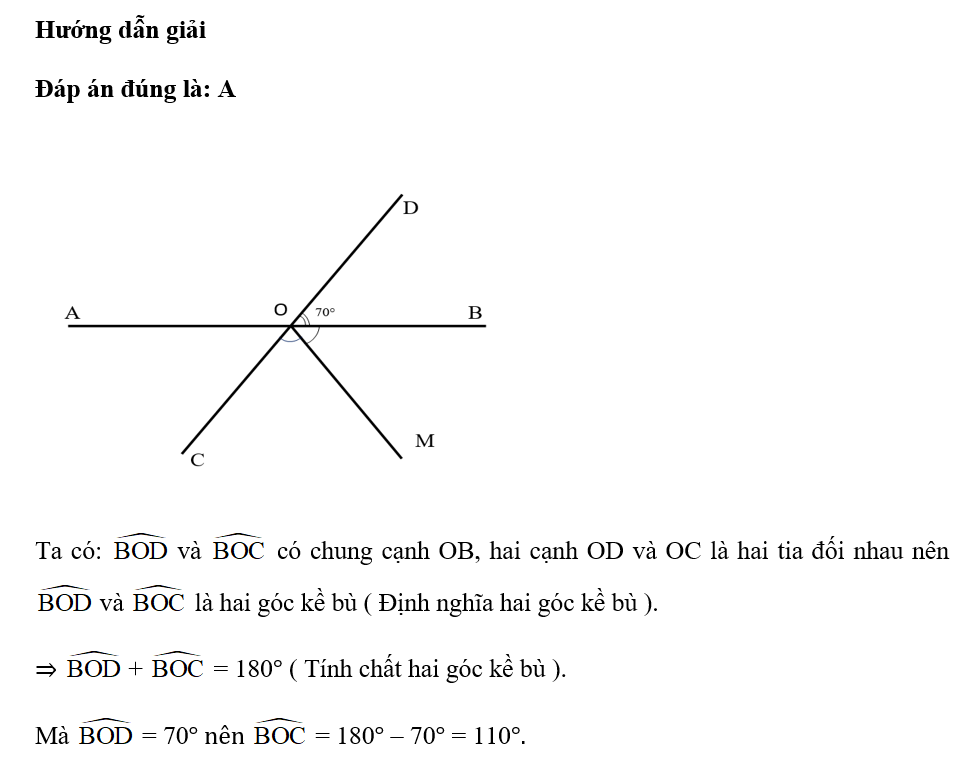
Cho hai đường thẳng AB và CD cắt nhau tại O sao cho $\hat{BOD}$ = 60°. OM là tia phân giác của góc BOC. Tính số đo góc MOB.

A. 120°;

B. 60°;

C. 30°;

D. 100°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\hat{BOD}$ và $\hat{BOC}$ có chung cạnh OB, hai cạnh OD và OC là hai tia đối nhau nên $\hat{BOD}$ và $\hat{BOC}$ là hai góc kề bù ( Định nghĩa hai góc kề bù ).

⇒ $\hat{BOD}$ + $\hat{BOC}$ = 180° ( Tính chất hai góc kề bù ).

Mà $\hat{BOD}$ = 60° nên $\hat{BOC}$ = 180° – 60° = 120°.

OM là tia phân giác của $\hat{BOC}$ nên $\hat{BOM} = \hat{COM} = \frac{1}{2} \hat{BOC} = \frac{1}{2} .120 ° = 60 °$ ( Tính chất tia phân giác của một góc).

Vậy $\hat{MOB} = 60 °$ . Đáp án đúng là B.

Câu 6:

Cho hai đường thẳng AB và CD cắt nhau tại O sao cho $\hat{BOD}$ = 70°. OM là tia phân giác của góc BOC. Tính số đo góc MOD.

A. 125°;

B. 135°;

C. 55°;

D. 70°.

Xem đáp án

Cho hai đường thẳng AB và CD cắt nhau tại O sao cho góc BOD= 70 độ. OM là tia phân giác (ảnh 1)

Cho hai đường thẳng AB và CD cắt nhau tại O sao cho góc BOD= 70 độ. OM là tia phân giác (ảnh 2)

Câu 7:

Cho $\hat{xAM} = 75 °$ và AM là tia phân giác của góc xAy. Tính số đo góc kề bù với góc xAy.

A. 30°;

B. 105°;

C. 125°;

D. 55°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

AM là tia phân giác của $\hat{xAy}$ nên $\hat{xAM} = \hat{yAM} = \frac{1}{2} \hat{xAy}$ ( Tính chất tia phân giác của 1 góc ).

Mà $\hat{xAM} = 75 °$ ⇒ $\hat{xAy}$ = 75°.2 = 150°.

Gọi $\hat{A_{1}}$ là góc kề bù với $\hat{xAy}$ ⇒ $\hat{A_{1}}$ + $\hat{xAy}$ = 180°.

⇒ $\hat{A_{1}}$ = 180° – 150° = 30°.

Vậy số đo góc kề bù với $\hat{xAy}$ là 30°. Đáp án đúng là A.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 7 KNTT Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của 1 góc (Phần 2) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của 1 góc (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương