9 câu hỏi trắc nghiệm thuộc Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác có đáp án (Thông hiểu)

Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác có đáp án

Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác có đáp án (Thông hiểu)

1490 lượt thi
9 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Câu 1: Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ đường thẳng song song với Oy cắt Oz ở M. Qua M kẻ đường thẳng song song với Ox cắt Oy ở B. Chọn câu đúng.

A. $O A > O B; M A > M B$

B. $O A = O B; M A = M B$

C. $O A < O B; M A < M B$

D. $O A < O B; M A = M B$

Xem đáp án

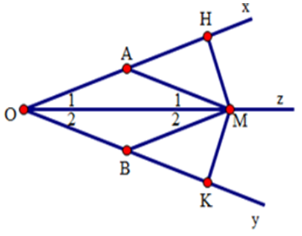
Ta có:

$\hat{M_{1}} = \hat{O_{2}}$ (hai góc so le trong )

$\hat{M_{2}} = \hat{O_{1}}$ ( hai góc so le trong )

$\hat{O_{1}} = \hat{O_{2}}$ (do Oz là tia phân giác của góc xOy)

Do đó $\hat{M_{2}} = \hat{M_{1}}$

Xét tam giác AOM và tam giác BOM có:

$\hat{M_{2}} = \hat{M_{1}}$ (cmt)

OM cạnh chung

$\hat{O_{1}} = \hat{O_{2}}$ (cmt)

Do đó: $O A = O B; M A = M B$ (các cặp cạnh tương ứng)

Đáp án cần chọn là B

Câu 2:

Câu 2: Cho góc xOy có tia phân giác Oz. Trên Oz lấy điểm E, vẽ đường thẳng qua E vuông góc với Ox tại K, cắt Oy tại N. Vẽ đường thẳng qua E vuông góc với Oy tại H cắt Ox tại M. Chọn câu đúng.

A. $O K < O H, K N < H M$

B. $O K = O H, K N < H M$

C. $O K < O H, K N > H M$

D. $O K = O H, K N = H M$

Xem đáp án

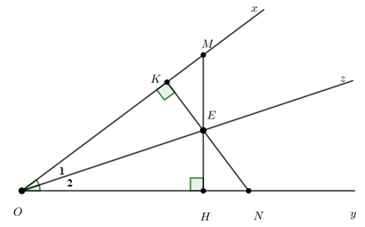
Vì Oz là tia phân giác của $\hat{x O y}$ nên $\hat{O_{1}} = \hat{O_{2}}$

Xét tam giác OKE và tam giác OHE có:

$\begin{array}{l} \hat{E K O} = \hat{E H O} = 90^{o} (g t) \\ O E c h u n g \end{array}$

$\hat{O_{1}} = \hat{O_{2}}$ (cmt)

$\Rightarrow Δ O K E = Δ O H E$ (cạnh huyền - góc nhọn)

Do đó : $O K = O H$ (hai cạnh tương ứng)

Xét tam giác OKN và tam giác OHM có:

$\hat{E K O} = \hat{E H O} = 90^{o}$ (gt)

$O K = O H$ (cmt)

$\hat{M O N}$ chung

$\Rightarrow Δ O K N = Δ O H M (g . c . g)$

Do đó: $K N = H M$ (hai cạnh tương ứng)

Đáp án cần chọn là D

Câu 3:

Câu 3: Cho tam giác ABC có $A B < A C$ . Tia phân giác của góc A cắt BC ở K. Từ B kẻ đường thẳng vuông góc với AK cắt H tại AC ở D. Chọn câu sai.

A. $H B = H D$

B. $H B = A D$

C. $A B = A D$

D. $\hat{A B H} = \hat{A D H}$

Xem đáp án

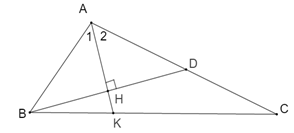
Vì AK là tia phân giác của $\hat{B A C}$ nên $\hat{A_{1}} = \hat{A_{2}}$

Theo giả thiết ta có:

Xét tam giác AHB và tam giác AHD có: $B H ⊥ A K \Rightarrow B D ⊥ A K \Rightarrow \hat{A H B} = \hat{A H D} = 90^{o}$

$\hat{A_{1}} = \hat{A_{2}}$ (cmt)

AH là cạnh chung

$\hat{A H B} = \hat{A H D} = 90^{o}$

$\Rightarrow Δ A H B = Δ A H D (g . c . g) \Rightarrow H B = H D; A B = A D$ (hai cạnh tương ứng); $\hat{A B H} = \hat{A D H}$ (hai góc tương ứng)

Đáp án cần chọn là B

Câu 4:

Câu 4: Cho tam giác DEF và tam giác HKG có $\hat{D} = \hat{H}, \hat{E} = \hat{K}, D E = H K$ . Biết $\hat{F} = 80^{o}$ . Số đo góc G là:

A. $70^{o}$

B. $80^{o}$

C. $90^{o}$

D. $100^{o}$

Xem đáp án

Xét tam giác DEF và tam giác HKG có

$\hat{D} = \hat{H}$ (GT)

$D E = H K$ (GT)
$\hat{E} = \hat{K}$ (GT)

$\Rightarrow Δ D E F = Δ H K G (g - c - g)$

$\Rightarrow \hat{G} = \hat{F} = 80^{o}$ (hai góc tương ứng)

Đáp án cần chọn là B

Câu 5:

Câu 5: Cho tam giác DEF và tam giác HKG có $\hat{D} = \hat{H}, \hat{E} = \hat{K}, D E = K G$ . Biết $\hat{F} = 75^{o}$ . Số đo góc H là:

A. $70^{o}$

B. $75^{o}$

C. $90^{o}$

D. $100^{o}$

Xem đáp án

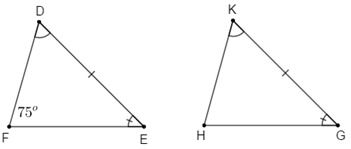
Xét tam giác DEF và tam giác HKG có:

$\begin{array}{l} \hat{D} = \hat{H} \\ \hat{E} = \hat{K} \\ D E = K G \\ \Rightarrow Δ D EF = Δ K G H (g . c . g) \end{array}$

$\Rightarrow \hat{H} = \hat{F} = 75^{o}$ (hai góc tương ứng)

Đáp án cần chọn là B

Câu 6:

Câu 6: Cho tam giác ABC và tam giác DEF có $A B = D E; \hat{B} = \hat{E}, \hat{A} = \hat{D}$ . Biết $A C = 6 c m$ . Độ dài DF là:

A. 4cm

B. 5cm

C. 6cm

D. 7cm

Xem đáp án

Xét tam giác ABC và tam giác DEF có:

$\begin{array}{l} A B = D E \\ \hat{B} = \hat{E} \\ \hat{A} = \hat{D} \\ \Rightarrow Δ A B C = Δ D EF(g-c-g) \end{array}$

$\Rightarrow D E = A C = 6 c m$ (hai cạnh tương ứng)

Đáp án cần chọn là C

Câu 7:

Câu 7: Cho tam giác MNP và tam giác DEF có $M N = EF; \hat{M} = \hat{F}, \hat{N} = \hat{E}$ . Biết $E D = 9 c m$ . Độ dài NP là:

A. 7cm

B. 8cm

C. 9cm

D. 10cm

Xem đáp án

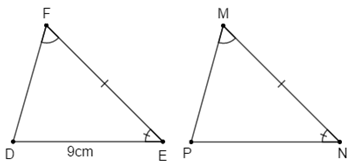
Xét tam giác MNP và tam giác DEF có:

$\begin{array}{l} M N = EF \\ \hat{M} = \hat{F} \\ \hat{N} = \hat{E} \\ \Rightarrow Δ M N P = Δ F E D (g . c . g) \end{array}$

$\Rightarrow N P = E D = 9 c m$ (hai cạnh tương ứng)

Đáp án cần chọn là C

Câu 8:

Câu 8: Cho tam giác ABC vuông tại A có $A B = A C$ . Qua A kẻ đường thẳng xy sao cho B, C nằm cùng phía với xy. Kẻ BD và CE vuông góc với xy. Chọn câu đúng.

A. $D E = B D + C E$

B. $D E = B D - C E$

C. $C E = B D + D E$

D. $C E = B D - D E$

Xem đáp án

Ta có: $\hat{A_{1}} + \hat{A_{2}} = 90^{o}$ (do $\hat{B A C} = 90^{o}$ )

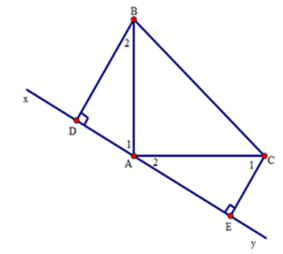
Mà $\hat{A_{1}} + \hat{B_{2}} = 90^{o}$ vì tam giác ABD vuông tại D

$\Rightarrow \hat{A_{2}} = \hat{B_{2}}$ (cùng phụ với $\hat{A_{1}}$ )

Lại có: $\hat{A_{2}} + \hat{C_{1}} = 90^{o}$ vì tam giác ACE vuông tại E

$\Rightarrow \hat{A_{1}} = \hat{C_{1}}$ (cùng phụ với $\hat{A_{2}}$ )

Xét tam giác BDA và tam giác AEC có:

$\begin{array}{l} \hat{D} = \hat{E} = 90^{o} \\ A B = A C (g t) \\ \hat{A_{1}} = \hat{C_{1}} (c m t) \end{array}$

$\Rightarrow Δ B D A = Δ A E C$ (cạnh huyền-góc nhọn)

$\Rightarrow B D = A E$ , $C E = A D$ ( hai cạnh tương ứng)

Do đó: $D E = A D + A E = C E + B D$

Đáp án cần chọn là A

Câu 9:

Câu 9: Cho hai đoạn thẳng AB,CD song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song AC,BD. Chọn câu đúng.

A. $A B = C D$

B. $A B > C D$

C. $A B < C D$

D. $A C > B D$

Xem đáp án

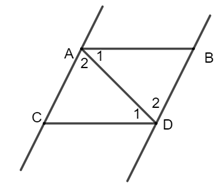
Kẻ đoạn thẳng AD

Vì AB//CD (gt) nên $\hat{A_{1}} = \hat{D_{1}}$ (hai góc so le trong)

Vì AC//BD (gt) nên $\hat{A_{2}} = \hat{D_{2}}$ (hai góc so le trong)

Xét tam giác ABD và tam giác DCA có:

$\hat{A_{1}} = \hat{D_{1}}$ (cmt)

AD là cạnh chung

$\hat{A_{2}} = \hat{D_{2}}$ (cmt)

$\Rightarrow Δ A B D = Δ D C A (g . c . g) \Rightarrow A B = C D, A C = B D$ (hai cạnh tương ứng)

Đáp án cần chọn là A

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác có đáp án

Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương