Trắc nghiệm Trường hợp bằng nhau thứ hai của tam giác có đáp án (Vận dụng)
-
2330 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Câu 1: Cho tam giác ABC, kẻ BD vuông góc với AC, kẻ CE vuông góc AB. Trên tia đối của tia BD lấy điểm H sao cho . Trên tia đối của tia CE, lấy điểm K sao cho . So sánh AH, AK
 Xem đáp án
Xem đáp án
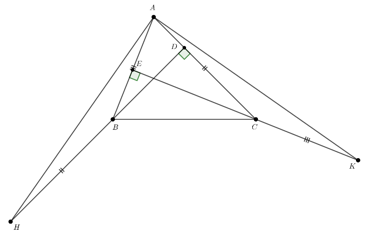
Ta có: là góc ngoài đỉnh B của nên
(1)
là góc ngoài đỉnh C của
(2)
Từ (1) và (2) suy ra
Xét và có:
(cmt)
(hai cạnh tương ứng)
Đáp án cần chọn là C
Câu 2:
Câu 2: Cho tam giác ABC có M,N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC lấy D sao cho . Trên tia đối của tia NB lấy điểm E sao cho
(I)
(II)
(III) A,D,E thẳng hàng
(IV) A là trung điểm của đoạn thẳng DE
Số khẳng định đúng trong các khẳng định trên là:
 Xem đáp án
Xem đáp án
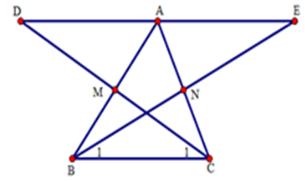
(I) Xét và có:
(hai góc đối đỉnh)
nên (I) đúng
(II) Xét và có:
(hai góc đối đỉnh)
nên (II) đúng
(III) Do nên (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AD//BC
Do nên ( hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AE//BC
Như vậy qua A có hai đường thẳng AD,AE cùng song song với BC.
Do đó D,A,E thẳng hàng (1) nên (III) đúng
(IV) Ta có (do ); (do ) nên (2)
Từ (1) và (2) suy ta A là trung điểm DE
Vậy cả (I),(II),(III),(IV) đều đúng
Đáp án cần chọn là C
Câu 3:
Câu 3: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E, F lần lượt là điểm thuộc đoạn AD và BC sao cho . Cho , tính EF.
 Xem đáp án
Xem đáp án
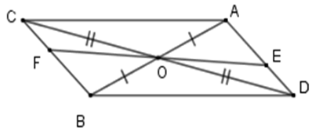
Xét tam giác OBC và OAD có:
(đối đỉnh)
nên (hai góc tương ứng)
Xét tam giác OBF và OAE có:
(cmt)
nên (hai cạnh tương ứng) và (hai góc tương ứng)
Mà (hai góc kề bù) nên
Suy ra ba điểm F;O;E thẳng hàng và nên O là trung điểm của EF nên
Đáp án cần chọn là A
Câu 4:
Câu 4: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E,F lần lượt là điểm thuộc đoạn AD và BC sao cho . Cho , tính EF.
 Xem đáp án
Xem đáp án
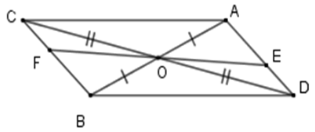
Xét tam giác OBC và OAD có:
(đối đỉnh)
nên (hai góc tương ứng)
Xét tam giác OBF và OAE có:
(cmt)
nên (hai cạnh tương ứng) và (hai góc tương ứng)
Mà (hai góc kề bù) nên
Suy ra ba điểm F;O;E thẳng hàng và nên O là trung điểm của EF nên
Đáp án cần chọn là B
Câu 5:
Câu 5: Cho tam giác ABC có , M là trung điểm của AC. Trên tia đối của tia MB lấy K sao cho . Chọn câu đúng nhất.
 Xem đáp án
Xem đáp án
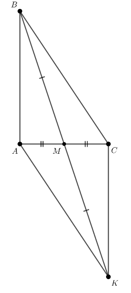
Xét và có:
(vì M là trung điểm AC)
(gt)
(hai góc đối đỉnh)
(hai góc tương ứng)
Mà (vì vuông tại A) suy ra
Do đó : nên A đúng
Xét và có
(vì M là trung điểm của AC)
(hai góc đối đỉnh)
(hai cạnh tương ứng) (C đúng)
(hai góc tương ứng)
Mà và ở vị trí so le trong nên AK//BC (B đúng)
Đáp án cần chọn là D
Câu 6:
Câu 6.1: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho . Chọn câu đúng.
 Xem đáp án
Xem đáp án
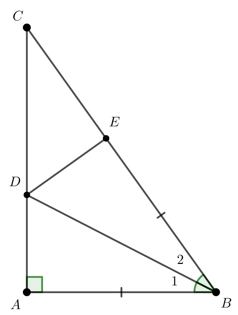
Xét và có:
(vì BD là tia phân giác )
BD cạnh chung
Đáp án cần chọn là A
Câu 7:
Câu 6.2: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho . Trên tia đối của tia DE lấy điểm M sao cho. So sánh EC và AM.
 Xem đáp án
Xem đáp án
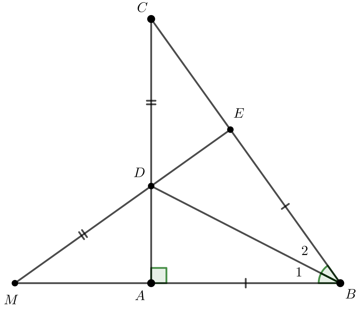
Sử dụng kết quả câu trước suy ra (hai cạnh tương ứng). Nối AM
Xét và có:
(hai góc đối đỉnh)
(hai cạnh tương ứng bằng nhau)
Đáp án cần chọn là B
Câu 8:
Câu 6.3: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho .
Trên tia đối của tia DE lấy điểm M sao cho . Nối AE, so sánh số đo .
 Xem đáp án
Xem đáp án
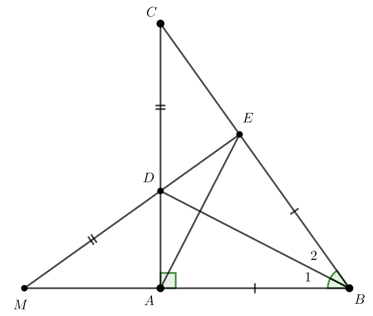
Sử dụng kết quả câu trước suy ra (Các cạnh tương ứng)
Ta có:
Cộng (1) và (2) theo vế với vế ta được hay
Xét và có:
AE chung
(hai góc tương ứng)
Đáp án cần chọn là C
Câu 9:
Câu 7.1: Cho điểm A nằm trong góc nhọn xOy. Vẽ AH vuông góc với Ox, trên tia đối của HA lấy điểm B sao cho . Vẽ AK vuông góc với Oy, trên tía đối của KA lấy điểm C sao cho . So sánh OB, OC.
 Xem đáp án
Xem đáp án
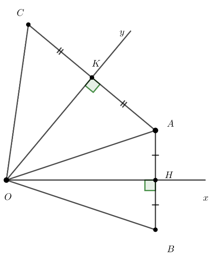
Xét và có:
OH cạnh chung
(hai cạnh tương ứng) (1)
Xét và có:
Cạnh OK chung
(hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra
Đáp án cần chọn là B
Câu 10:
Câu 7.2: Cho điểm A nằm trong góc nhọn xOy. Vẽ AH vuông góc với Ox, trên tia đối của HA lấy điểm B sao cho . Vẽ AK vuông góc với Oy, trên tía đối của KA lấy điểm C sao cho . Biết . Tính .
 Xem đáp án
Xem đáp án
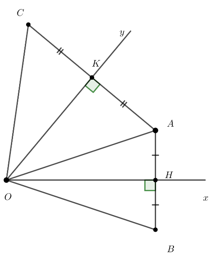
Sử dụng kết quả câu trước ta có: ,
Vì suy ra (hai góc tương ứng)
Vì suy ra ( hai góc tương ứng)
Ta có:
(do và )
Đáp án cần chọn là C
