Trắc nghiệm Trường hợp bằng nhau thứ hai của tam giác có đáp án (Thông hiểu)
-
2329 lượt thi
-
14 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Câu 1: Cho đoạn thẳng BD và EC vuông góc với nhau tại A sao cho . Phát biểu nào trong các phát biểu sau đây sai:
 Xem đáp án
Xem đáp án
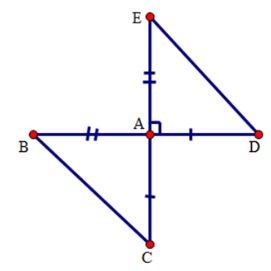
Xét hai tam giác AED và tam giác ABC có:
(2 góc đối đỉnh)
nên A đúng
Suy ra (2 cạnh tương ứng) nên B đúng ; (hai góc tương ứng ) nên D đúng
Đáp án cần chọn là C
Câu 2:
Câu 2: Cho đoạn thẳng BD và EC cắt nhau tại A sao cho . Phát biểu nào trong các phát biểu sau đây sai:
 Xem đáp án
Xem đáp án
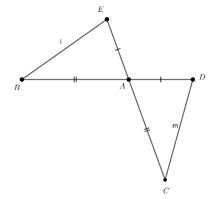
Xét và có:
(hai góc đối đỉnh)
nên A đúng
(hai cạnh tương ứng) nên B đúng
(hai góc tương ứng ) nên D đúng
Đáp án cần chọn là C
Câu 3:
Câu 3.1: Cho hai đường thẳng xx'; yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C, D sao cho O là trung điểm CD . Chọn câu đúng:
 Xem đáp án
Xem đáp án
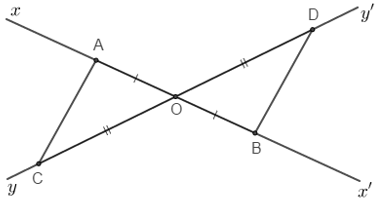
Xét và có:
(vì O là trung điểm AB)
(vì O là trung điểm CD)
(hai góc đối đỉnh)
Đáp án cần chọn là D
Câu 4:
Câu 3.2: Cho hai đường thẳng xx' ,yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C, D sao cho O là trung điểm CD . So sánh AC và BD
 Xem đáp án
Xem đáp án
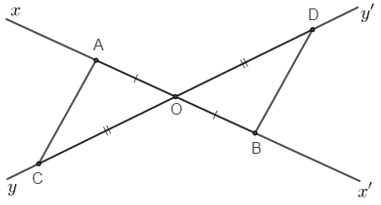
Xét và có:
(vì O là trung điểm AB)
(vì O là trung điểm CD)
(hai góc đối đỉnh)
(hai cạnh tương ứng)
Đáp án cần chọn là A
Câu 5:
Câu 4: Cho tam goác DEF và tam giác HKG có , biết . Số đo góc H là:
 Xem đáp án
Xem đáp án
Xét tam giác DEF và tam giác HKF có:
(hai góc tương ứng)
Đáp án cần chọn là A
Câu 6:
Câu 5: Cho tam goác DEF và tam giác MNP có , biết . Số đo góc M là:
 Xem đáp án
Xem đáp án
Xét và có:
(hai góc tương ứng)
Đáp án cần chọn là D
Câu 7:
Câu 6: Cho tam giác ABC có , tia phân giác BD của góc B . Trên cạnh BC lấy điểm E sao cho . Hai góc nào sau đây bằng nhau:
 Xem đáp án
Xem đáp án
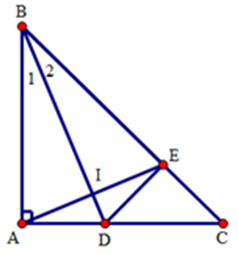
Xét tam giác BDA cà BDE có:
(do BD là tia phân giác của góc B)
BD là cạnh chung
(hai góc tương ứng)
Trong các tam giác ABC và EDC vuông tại A và E, ta có:
và , suy ra
Đáp án cần chọn là C
Câu 8:
Câu 7: Cho tam giác ABC có , tia phân giác BD của góc B . Trên cạnh BC lấy điểm E sao cho . Tính số đo góc EDC
 Xem đáp án
Xem đáp án
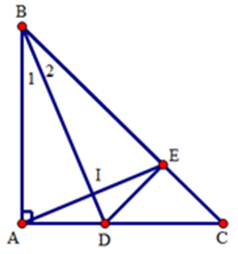
Xét tam giác BDA và BDE có:
( do BD là tia phân giác của góc B)
BD là cạnh chung
(hai góc tương ứng)
Trong các tam giác ABC và EDC vuông tại A và E, ta có:
và , suy ra
Đáp án cần chọn là C
Câu 9:
Câu 8: Cho đoạn thẳng AB, trên đường trung trực d của đoạn AB lấy điểm M. So sánh AM và BM
 Xem đáp án
Xem đáp án
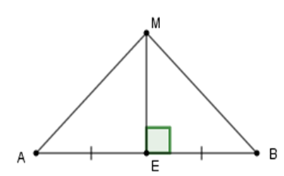
Đường trung trực của AB vuông góc với AB tại trung điểm E. Do đó
Xét tam giác MEA và tam giác MEB có:
(cmt)
Cạnh ME chung
(hai cạnh tương ứng)
Đáp án cần chọn là A
Câu 10:
Câu 9: Cho tam giác ABC có , tia phân giác của góc A cắt BC ở D. Trêm cạnh AC lấy E sao cho . Chọn câu đúng.
 Xem đáp án
Xem đáp án
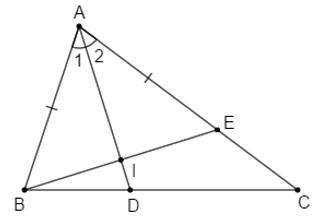
Gọi I là giao điểm của AD và BE
Xét và có:
AI cạnh chung
( Vì AD là phân giác )
(hai góc tương ứng)
(hai cạnh tương ứng) (1)
Mặt khác (hai góc kề bù)
Do đó (2)
Từ (1) và (2) suy ra AD là đường trung tuyến của BE
Đáp án cần chọn là C
Câu 11:
Câu 10.1: Cho tam giác ABC có , phân giác BD và CE cắt nhau tại O. Chọn câu đúng.
 Xem đáp án
Xem đáp án
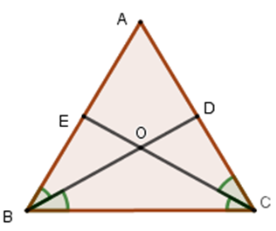
Vì BD và CE là tia phân giác của góc và nên và
Xét tam giác ABD và tam giác CBD có:
(cmt)
(hai góc tương ứng); (hai cạnh tương ứng) nên C sai
Mà (hai góc kề bù)
Nên . Do đó
Tương ứng
Đáp án cần chọn là D
Câu 12:
Câu 10.2: Cho tam giác ABC có , phân giác BD và CE cắt nhau tại O. Tính .
 Xem đáp án
Xem đáp án
Từ câu trước ta có: (hai góc tương ứng) (1)
Tương tự ta có: (hai góc tương ứng) (2)
Từ (1) và (2) ta có: . Mà
(định lý tổng ba góc trong tam giác ) nên
Lại có (cmt) nên ;
Xét tam giác BOC có ( định lý tổng ba góc trong tam giác )
Nên
Vậy
Đáp án cần chọn là C
Câu 13:
Câu 11.1: Cho góc nhọn xOy và Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A và trên tia Oy lấy điểm B sao cho . Gọi C là một điểm bất kì trên tia Oz. Chọn câu sai.
 Xem đáp án
Xem đáp án
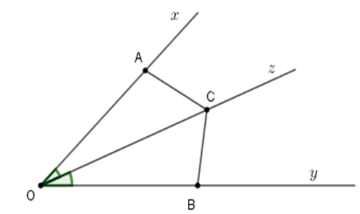
Xét tam giác AOC và BOC có:
(tính chất tia phân giác)
Cạnh OC chung
(hai cạnh tương ứng); ; (hai góc tương ứng)
Từ đó CO là tia phân giác của
Nên B,C,D đúng, A sai
Đáp án cần chọn là A
Câu 14:
Câu 11.2: Cho góc nhọn xOy và Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A và trên tia Oy lấy điểm B sao cho . Gọi C là một điểm bất kì trên tia Oz. Gọi I là giao của AB và Oz. Tính góc AIC.
 Xem đáp án
Xem đáp án
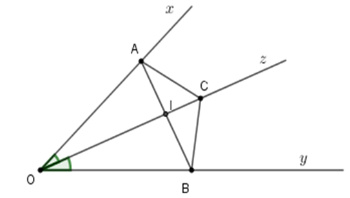
Xét tam giác AOI và BOI có:
(tính chất tia phân giác)
Cạnh OI chung
Do đó (hai góc tương ứng) mà nên
Hay
Đáp án cần chọn là B
