Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 3
-
5790 lượt thi
-
17 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Ba độ dài nào dưới đây là độ dài ba cạnh của một tam giác:
 Xem đáp án
Xem đáp án
+ Ta có: 2 + 4 = 6 nên bộ ba số 2cm, 4cm, 6cm không phải là độ dài ba cạnh của một tam giác.
+ Có 2 + 4 = 6 < 7 nên bộ ba số 2cm, 4cm, 7cm không phải độ dài ba cạnh của tam giác.
+ Ta có: 3 + 4 = 7 > 5; 3 + 5 = 8 > 4 và 4 + 5 = 9 > 3 nên bộ ba số 3cm, 4cm, 5 cm là độ dài ba cạnh của một tam giác.
+ Vì 2 + 3 = 5 nên bộ ba số 2cm, 3cm, 5 cm không phải độ dài ba cạnh của một tam giác.
Chọn đáp án C
Câu 2:
 Xem đáp án
Xem đáp án
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Do đó: đơn thức đồng dạng với đơn thức 2x2y là –5x2y.
Chọn đáp án C
Câu 3:
 Xem đáp án
Xem đáp án
có thì quan hệ giữa ba cạnh AB, AC, BC là:
Ta có:
Vì nên
Do đó: BC > AB > AC (trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn).
Chọn đáp án A
Câu 4:
 Xem đáp án
Xem đáp án
Biểu thức : , tại x = –1 có giá trị là:
Thay x = –1 vào biểu thức x2 + 2x ta được:
(–1)2 + 2.( –1) = 1 – 2 = –1
Chọn đáp án B
Câu 5:
 Xem đáp án
Xem đáp án
+) Thay x = –1 vào đa thức x + 1 ta được: –1 + 1 = 0 nên x = –1 là nghiệm của đa thức x + 1, đáp án A đúng.
+) Thay x = –1 vào đa thức x – 1 ta được: –1 – 1 = –2 0 nên x = –1 không là nghiệm của đa thức x – 1, B sai.
+) Thay x = –1 vào đa thức 2x + , ta được: 2.( –1) + = nên x = –1 không phải là nghiệm của đa thức 2x + , C sai.
+) Thay x = –1 vào đa thức x2 +1 ta được: (–1)2 + 1 = 2 0 nên x = –1 không phải là nghiệm của đa thức x2 + 1, D sai.
Chọn đáp án A
Câu 6:
Tam giác ABC có G là trọng tâm, AM là đường trung tuyến, ta có:
 Xem đáp án
Xem đáp án
Tam giác ABC có G là trọng tâm, AM là đường trung tuyến, ta có:
Tam giác ABC có AM là trung tuyến, G là trọng tâm
Nên theo tính chất trọng tâm ta có: AG = AM
Chọn đáp án D
Câu 8:
 Xem đáp án
Xem đáp án
Ta có: A – B = (2x2 + x – 1) – (x – 1) = 2x2 + x – 1 – x + 1 = 2x2
Chọn đáp án C
Câu 10:
Gọi M là trung điểm của BC trong tam giác ABC. AM gọi là đường gì của tam giác ABC ?
 Xem đáp án
Xem đáp án
Gọi M là trung điểm của BC trong tam giác ABC. AM gọi là đường gì của tam giác ABC ?
M là trung điểm của BC trong tam giác ABC nên AM là đường trung tuyến của tam giác ABC.
Chọn đáp án C
Câu 11:
Cho hình vẽ bên. So sánh AB, BC, BD ta được:
 Xem đáp án
Xem đáp án
Cho hình vẽ bên. So sánh AB, BC, BD ta được:
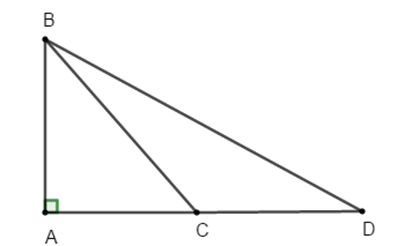
Vì BA AD và C nằm giữa A và D nên AC < AD
Do đó: AB < BC < BD (quan hệ đường xiên và hình chiếu).
Chọn đáp án A
Câu 12:
 Xem đáp án
Xem đáp án
Cho . Tại, đa thức A(x) – B(x) có giá trị là:
Ta có: A(x) – B(x) = (2x2 + x – 1) – (x – 1) = 2x2
Thay x = 1 vào biểu thức 2x2 ta được: 2.12 = 2
Vậy giá trị của biểu thức A(x) – B(x) tại x = 1 là 2.
Chọn đáp án ACâu 13:
Một giáo viên theo dõi thời gian giải bài toán (tính theo phút) của một lớp học và ghi lại:
|
10 |
5 |
4 |
7 |
7 |
7 |
4 |
7 |
9 |
10 |
|
6 |
8 |
6 |
10 |
8 |
9 |
6 |
8 |
7 |
7 |
|
9 |
7 |
8 |
8 |
6 |
8 |
6 |
6 |
8 |
7 |
a) Dấu hiệu cần tìm hiểu ở đây là gì?
b) Lập bảng tần số và tìm Mốt của dấu hiệu;
c) Tính thời gian trung bình của lớp.
 Xem đáp án
Xem đáp án
a) Dấu hiệu ở đây là thời gian giải bài toán của mỗi học sinh trong lớp. (0,25 điểm)
b) Bảng tần số (0,75 điểm)
|
Giá trị |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số |
2 |
1 |
6 |
8 |
7 |
3 |
3 |
N = 30 |
Mốt của dấu hiệu là 7. (0,25 điểm)
c) Số trung bình cộng là
(0,25 điểm)
Câu 15:
a) Rút gọn P(x), Q(x);
b) Chứng tỏ x = –1 là nghiệm của P(x), Q(x);
 Xem đáp án
Xem đáp án
a) P(x) = 2x3 – 2x + x2 + 3x + 2 = 2x3 + x2 + (–2x + 3x) + 2 = 2x3 + x2 + x + 2
Q(x) = 4x3 – 3x2 – 3x + 4x – 3x3 + 4x2 +1
= (4x3 – 3x3) + (–3x2 + 4x2) + (–3x + 4x) + 1
= x3 + x2 + x + 1
b) x = –1 là nghiệm của P(x) vì:
P(–1) = 2.(–1)3 + (–1)2 + (–1) + 2 = – 2 + 1 – 1 + 2 = 0 .
x = –1 là nghiệm của Q(x) vì:
Q(–1) = (–1)3 + (–1)2 + (–1) + 1 = –1 + 1 – 1 + 1 = 0 .
Câu 16:
Cho tam giác ABC. Ở phía ngoài tam giác đó vẽ các tam giác vuông cân tại A là ABD và ACE.
a) Chứng minh CD = BE và CD vuông góc với BE;
b) Lấy điểm K nằm trong tam giác ABD sao cho góc ABK bằng 300, BA = BK. Chứng minh: AK = KD.
 Xem đáp án
Xem đáp án
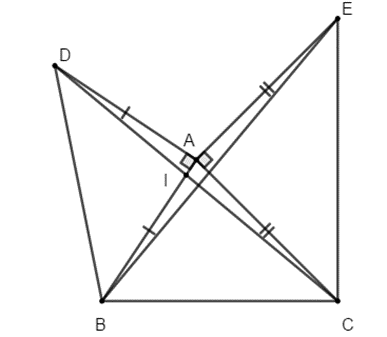
-Vẽ hình đúng được 0,5 điểm. (sai hình không chấm)
a) Xét tam giác ADC và tam giác ABE có:
AD = AB (Tam giác ADB cân tại A)
AC = AE (Tam giác ACE vuông tại A)
Do đó:
Suy ra DC = BE (2 cạnh tương ứng); (2 góc tương ứng)
Gọi I là giao điểm của DC và AB.
Ta có: (đối đỉnh); (c/m trên)
Mà (tam giác IAD vuông tại A) suy ra
Suy ra DC vuông góc với BE. (1 điểm)
b)
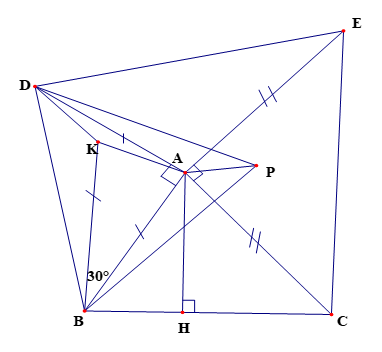
Vẽ tam giác đều BPD sao cho P và A nằm cùng phía đối với BD
Ta có: suy ra
Suy ra suy ra (1)
Tam giác BAK cân tại B có góc ABK = 300
Nên suy ra (2)
Từ (1) và (2) suy ra: nên tam giác KDA cân tại K suy ra KA = KD (1 điểm)
Câu 17:
 Xem đáp án
Xem đáp án
Ta có:
x2y2 – x2 + 2y2 – 2 = 0
x2(y2 – 1) + 2(y2 – 1) = 0
(y2 – 1).( x2 + 2) = 0
Vì x2 + 2 > 0 với mọi x
Do đó y2 – 1 = 0 = 1 hoặc y = –1
Vậy y {1; – 1} và x là một số thực tùy ý.
