Tích phân
-
635 lượt thi
-
40 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số f(x) liên tục trên đoạn \[\left[ {a;b} \right].\]Chọn mệnh đề sai?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 2:
Giả sử hàm số y=f(x) liên tục trên \[\left[ {a;b} \right]\;\]và k là một số thực trên R. Cho các công thức:
a) \[\mathop \smallint \limits_a^a f\left( x \right)dx = 0\]
b) \[\mathop \smallint \limits_a^b f\left( x \right)dx = \mathop \smallint \limits_b^a f\left( x \right)dx\]
c) \[\mathop \smallint \limits_a^b kf\left( x \right)dx = k\mathop \smallint \limits_a^b f\left( x \right)dx\]
Số công thức sai là:
 Xem đáp án
Xem đáp án
Dễ thấy các công thức a) đúng vì tích phân có hai cận bằng nhau thì có giá trị 0.
Công thức c) là đúng theo tính chất tích phân.
Công thức b) sai vì \[\mathop \smallint \limits_a^b f\left( x \right)dx = - \mathop \smallint \limits_b^a f\left( x \right)dx\]
Đáp án cần chọn là: A
Câu 3:
Cho hàm số f(x) có đạo hàm trên \[\left[ {1;4} \right]\;\]và \[f\left( 1 \right) = 2,f\left( 4 \right) = 10\]. Giá trị của \[I = \int\limits_1^4 {f\prime (x)dx} \] là
 Xem đáp án
Xem đáp án
\[I = \int\limits_1^4 {f\prime (x)dx} = f(x)|_1^4 = f(4) - f(1) = 10 - 2 = 8\]
Đáp án cần chọn là: C
Câu 4:
Cho hàm số y=f(x) liên tục trên đoạn \[\left[ {0;1} \right],\;\]có \[\mathop \smallint \limits_0^1 \left[ {3 - 2f\left( x \right)} \right]{\rm{d}}x = 5.\]. Tính \[\mathop \smallint \limits_0^1 f\left( x \right){\rm{d}}x\].
 Xem đáp án
Xem đáp án
Ta có
\[\mathop \smallint \limits_0^1 \left[ {3 - 2f\left( x \right)} \right]{\rm{d}}x = \mathop \smallint \limits_0^1 3dx - 2\mathop \smallint \limits_0^1 f(x)dx = 3x|_0^1 - 2\mathop \smallint \limits_0^1 f(x)dx = 3 - 2\mathop \smallint \limits_0^1 f(x)dx\]
Mặt khác
\[\mathop \smallint \limits_0^1 \left[ {3 - 2f\left( x \right)} \right]{\rm{d}}x = 5 \Rightarrow 3 - 2\,\mathop \smallint \limits_0^1 f\left( x \right){\rm{d}}x = 5 \Leftrightarrow \mathop \smallint \limits_0^1 f\left( x \right){\rm{d}}x = - \,1.\]
Đáp án cần chọn là: A
Câu 5:
Đặt \[F\left( x \right) = \mathop \smallint \limits_1^x tdt\]. Khi đó F′(x) là hàm số nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 6:
Cho hàm số \[F\left( x \right) = \mathop \smallint \limits_1^x \left( {t + 1} \right)dt\]. Giá trị nhỏ nhất của F(x) trên đoạn \[\left[ { - 1;1} \right]\;\]là:
 Xem đáp án
Xem đáp án
Ta có:
\[F(x) = \int\limits_1^x {(t + 1)dt} = \left( {\frac{{{t^2}}}{2} + t} \right)\left| {_1^x} \right. = \frac{{{x^2}}}{2} + x - \frac{1}{2} - 1 = \frac{{{x^2}}}{2} + x - \frac{3}{2}\]
Hàm số\[y = F\left( x \right)\]là hàm số bậc hai, hệ số a>0 nên nó đạt GTNN tại\[x = - 1 \in \left[ { - 1;1} \right]\]
Khi đó\[F( - 1) = \frac{1}{2} + ( - 1) - \frac{3}{2} = - 2\]
Đáp án cần chọn là: D
Câu 7:
Cho hai hàm số \[f\left( x \right) = {x^2}\] và \[g(x) = {x^3}\]. Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Vì \[f\left( x \right) = {x^2} \ge 0,\forall x \in \left[ {0;1} \right]\] nên\[\mathop \smallint \limits_0^1 f\left( x \right)dx \ge 0\] Do đó A đúng, D sai.
Vì \[g\left( x \right) = {x^3} \ge 0,\forall x \in \left[ {0;1} \right]\] nên\[\mathop \smallint \limits_0^1 g\left( x \right)dx \ge 0\] Do đó B sai.
Vì \[{x^2} \ge {x^3}\] trên\[\left[ {0;1} \right]\] nên\[\mathop \smallint \limits_0^1 f\left( x \right)dx \ge \mathop \smallint \limits_0^1 g\left( x \right)dx\] Do đó C sai.
Đáp án cần chọn là: A
Câu 8:
Giả sử f(x) là hàm liên tục trên R và các số thực a<b
 Xem đáp án
Xem đáp án
Dựa vào các đáp án ta có nhận xét sau:
\[\mathop \smallint \limits_a^c f(x)dx = \mathop \smallint \limits_a^b f(x)dx + \mathop \smallint \limits_b^c f(x)dx\] => A đúng
\[\mathop \smallint \limits_a^b f(x)dx = \mathop \smallint \limits_a^c f(x)dx - \mathop \smallint \limits_b^c f(x)dx\] B đúng
\[\mathop \smallint \limits_a^b f(x)dx = \mathop \smallint \limits_b^a f(x)dx + \mathop \smallint \limits_a^c f(x)dx\] C sai
\[\mathop \smallint \limits_a^b cf(x)dx = - c\mathop \smallint \limits_b^a f(x)dx\] D đúng.
Đáp án cần chọn là: C
Câu 9:
Nếu \[f\left( 1 \right) = 12,f\prime (x)\;\] liên tục và \[\int\limits_1^4 {f\prime (x)dx = 17} \]thì giá trị của f(4) bằng:
 Xem đáp án
Xem đáp án
Ta có:
\[\int\limits_1^4 {f\prime (x)dx = 17} \Rightarrow f(x)|_1^4 = 17 \Rightarrow f(4) - f(1) = 17\]
\[ \Rightarrow f(4) - 12 = 17 \Rightarrow f(4) = 29\]
Đáp án cần chọn là: A
Câu 10:
Cho \[\mathop \smallint \limits_2^5 f\left( x \right)dx = 10\], khi dó \[\mathop \smallint \limits_5^2 \left[ {2 - 4f\left( x \right)} \right]dx\] có giá trị là:
 Xem đáp án
Xem đáp án
Ta có:
\[\mathop \smallint \limits_5^2 \left[ {2 - 4f\left( x \right)} \right]dx = \mathop \smallint \limits_5^2 2dx - 4\mathop \smallint \limits_5^2 f(x)dx = 2x\left| {_5^2} \right. + 4\mathop \smallint \limits_2^5 f(x)dx = 2.2 - 2.5 + 4.10 = 34\]
Đáp án cần chọn là: B
Câu 11:
Cho hàm số f(x) liên tục trên R thỏa mãn \[\mathop \smallint \limits_a^d f\left( x \right)dx = 10,\mathop \smallint \limits_b^d f\left( x \right)dx = 18,\mathop \smallint \limits_a^c f\left( x \right)dx = 7\]. Giá trị của \[\mathop \smallint \limits_b^c f\left( x \right)dx\] là:
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{*{20}{l}}{\mathop \smallint \limits_a^d f\left( x \right)dx = \mathop \smallint \limits_a^c f\left( x \right)dx + \mathop \smallint \limits_c^b f\left( x \right)dx + \mathop \smallint \limits_b^d f\left( x \right)dx}\\{ \Rightarrow \mathop \smallint \limits_c^b f\left( x \right)dx = \mathop \smallint \limits_a^d f\left( x \right)dx - \mathop \smallint \limits_a^c f\left( x \right)dx - \mathop \smallint \limits_b^d f\left( x \right)dx}\\{ \Rightarrow \mathop \smallint \limits_c^b f\left( x \right)dx = 10 - 7 - 18 = - 15 \Rightarrow \mathop \smallint \limits_b^c f\left( x \right)dx = 15}\end{array}\]
Đáp án cần chọn là: C
Câu 12:
Cho biết \[\mathop \smallint \limits_1^3 f\left( x \right)dx = - 2,\mathop \smallint \limits_1^4 f\left( x \right)dx = 3,\mathop \smallint \limits_1^4 g\left( x \right)dx = 7\]. Chọn khẳng định sai?
 Xem đáp án
Xem đáp án
Ta có:\[\mathop \smallint \limits_1^4 \left[ {f\left( x \right) + g\left( x \right)} \right]dx = \mathop \smallint \limits_1^4 f\left( x \right)dx + \mathop \smallint \limits_1^4 f\left( x \right)dx = 10\] nên A đúng.
\[\mathop \smallint \limits_1^4 f\left( x \right)dx = \mathop \smallint \limits_1^3 f\left( x \right)dx + \mathop \smallint \limits_3^4 f\left( x \right)dx \Rightarrow \mathop \smallint \limits_3^4 f\left( x \right)dx = \mathop \smallint \limits_1^4 f\left( x \right)dx - \mathop \smallint \limits_1^3 f\left( x \right)dx = 3 - \left( { - 2} \right) = 5\]nên C đúng, B sai.
\[\mathop \smallint \limits_1^4 \left[ {4f\left( x \right) - 2g\left( x \right)} \right]dx = 4\mathop \smallint \limits_1^4 f\left( x \right)dx - 2\mathop \smallint \limits_1^4 g\left( x \right)dx = - 2\]nên D đúng.
Đáp án cần chọn là: B
Câu 13:
Giả sử A,B là các hằng số của hàm số \[f(x) = Asin\pi x + B{x^2}\] Biết \[\mathop \smallint \limits_0^2 f\left( x \right)dx = 4\]giá trị của B là:
 Xem đáp án
Xem đáp án
Ta có:\[\mathop \smallint \limits_0^2 f\left( x \right)dx = 4 \Leftrightarrow \mathop \smallint \limits_0^2 \left( {A\sin \pi x + B{x^2}} \right)dx = 4\]
\[ \Leftrightarrow \left( { - \frac{A}{\pi }cos\pi x + \frac{B}{3}{x^3}} \right)\left| {_0^2} \right. = 4 \Leftrightarrow \frac{B}{3}{.2^3} = 4 \Leftrightarrow B = \frac{3}{2}\]
Đáp án cần chọn là: C
Câu 14:
Cho số thực a thỏa mãn \(\int\limits_{ - 1}^a {{e^{x + 1}}} dx = {e^2} - 1\), khi đó a có giá trị bằng
 Xem đáp án
Xem đáp án
Ta có\(\int\limits_{ - 1}^a {{e^{x + 1}}} dx = {e^2} - 1 = {e^{x + 1}}\left| {_{ - 1}^a} \right. = {e^{a + 1}} - 1\)
Vậy yêu cầu bài toán trở thành\[{e^{a + 1}} - 1 = {e^2} - 1 \Leftrightarrow a + 1 = 2 \Leftrightarrow a = 1\]
Đáp án cần chọn là: A
Câu 15:
Trong các tích phân sau, tích phân nào có giá trị khác 22?
 Xem đáp án
Xem đáp án
+)\(\int\limits_0^1 {2dx = 2x\left| {_0^1} \right.} = 20\)
+)\(\int\limits_0^2 {xdx = \frac{{{x^2}}}{2}\left| {_0^2} \right.} = 2\)
+)\(\int\limits_0^\pi {{\mathop{\rm s}\nolimits} {\rm{inx}}dx = - cosx\left| {_0^\pi } \right.} = 2\)
Do đó ta dự đoán chỉ có đáp án A là kết quả khác 2.
Đáp án cần chọn là: A
Câu 16:
Tích phân \[I = \mathop \smallint \limits_1^2 {x^5}dx\] có giá trị là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 17:
Cho hàm số bậc ba \[f\left( x \right) = {x^3} + a{x^2} + bx + c\,\,\,\left( {a,\,\,b,\,\,c \in \mathbb{R}} \right)\] thỏa mãn: \[f\left( 1 \right) = 10,f\left( 2 \right) = 20.\]. Khi đó \(\int\limits_0^3 {f'\left( x \right)dx} \) bằng:
 Xem đáp án
Xem đáp án
Theo đề bài ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{f(1) = 10}\\{f(2) = 20}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 + a + b + c = 10}\\{{2^3} + {2^2}.a + 2b + c = 20}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a + b + c = 9}\\{4a + 2b + c = 12}\end{array}} \right. \Rightarrow 3a + b = 3\end{array}\)
\( \Rightarrow \int\limits_0^3 {f'\left( x \right)dx} = f(x)\left| {_0^3} \right. = f(3) - f(0)\)
\[ = {3^3} + {3^2}.a + 3b + c - c = 27 + 9a + 3b\]
\[ = 27 + 3(3a + b) = 27 + 3.3 = 36\]
Đáp án cần chọn là: D
Câu 18:
Giá trị của b để \(\int\limits_1^b {\left( {2x - 6} \right)} dx = 0\) là:
 Xem đáp án
Xem đáp án
Ta có:
\(\int\limits_1^b {\left( {2x - 6} \right)} dx = 0 \Leftrightarrow \int\limits_1^b {2xdx - } \int\limits_1^b {6dx = 0 \Leftrightarrow {x^2}\left| {_1^b} \right.} - 6x\left| {_1^b} \right. = 0\)
\[ \Leftrightarrow {b^2} - 1 - 6b + 6 = 0 \Leftrightarrow {b^2} - 6b + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{b = 1}\\{b = 5}\end{array}} \right.\]
Đáp án cần chọn là: D
Câu 19:
Nếu \[\mathop \smallint \limits_1^2 \frac{{dx}}{{x + 3}}\]được viết dưới dạng \[ln\frac{a}{b}\;\] với a,b là các số tự nhiên và ước chung lớn nhất của a,b là 1. Chọn khẳng định sai:
 Xem đáp án
Xem đáp án
Ta có:\[\int\limits_1^2 {\frac{{dx}}{{x + 3}}} = \ln \left| {x + 3} \right|\left| {_1^2} \right. = ln5 - ln4 = ln\frac{5}{4}\]
Do đó\[a = 5,b = 4\]
Khi đó:\[3a - b = 3.5 - 4 = 11 < 12\] nên A đúng.
\[a + 2b = 5 + 2.4 = 13\] nên B đúng.
\[a - b = 5 - 4 = 1 < 2\] nên C sai.
\[{a^2} + {b^2} = {5^2} + {4^2} = 41\] nên D đúng.
Đáp án cần chọn là: C
Câu 20:
Nếu \[\mathop \smallint \limits_0^1 \left[ {{f^2}\left( x \right) - f\left( x \right)} \right]dx = 5\]và \[\mathop \smallint \limits_0^1 {\left[ {f\left( x \right) + 1} \right]^2}dx = 36\]thì \(\int\limits_0^1 {f\left( x \right)dx} \) bằng:
 Xem đáp án
Xem đáp án
Ta có:\[\mathop \smallint \limits_0^1 \left[ {{f^2}\left( x \right) - f\left( x \right)} \right]dx = 5\]
\[\begin{array}{l}\mathop \smallint \limits_0^1 {\left[ {f\left( x \right) + 1} \right]^2}dx = 36 \Leftrightarrow \mathop \smallint \limits_0^1 [{f^2}(x) + 2f(x) + 1]dx = 36\\ \Rightarrow \mathop \smallint \limits_0^1 [{f^2}(x) + 2f(x) + 1]dx - \mathop \smallint \limits_0^1 [{f^2}(x) - f(x)]dx = 36 - 5\\ \Leftrightarrow \mathop \smallint \limits_0^1 [3f(x) + 1]dx = 31 \Leftrightarrow 3\mathop \smallint \limits_0^1 f(x)dx + \mathop \smallint \limits_0^1 dx = 31\\ \Leftrightarrow 3\mathop \smallint \limits_0^1 f(x)dx + x\left| {_0^1} \right. = 31 \Leftrightarrow 3\mathop \smallint \limits_0^1 f(x)dx + 1 = 31\\ \Leftrightarrow 3\mathop \smallint \limits_0^1 f(x)dx = 30 \Leftrightarrow \mathop \smallint \limits_0^1 f(x)dx = 10.\end{array}\]
Đáp án cần chọn là: D
Câu 21:
Cho hàm số f(x) liên tục trên \[\left( {0; + \infty } \right)\;\]và thỏa mãn \[2f(x) + xf\left( {\frac{1}{x}} \right) = x\;\] với mọi x>0. Tính \[\mathop \smallint \limits_{\frac{1}{2}}^2 f\left( x \right)dx\].
 Xem đáp án
Xem đáp án
Ta có: \[2f\left( x \right) + xf\left( {\frac{1}{x}} \right) = x\] với\[x = \frac{1}{t}\]ta có \[2f\left( {\frac{1}{t}} \right) + \frac{1}{t}f\left( t \right) = \frac{1}{t}\]
\[ \Rightarrow f\left( {\frac{1}{t}} \right) = \frac{1}{2}\left( {\frac{1}{t} - \frac{1}{t}f\left( t \right)} \right)\]
\[ \Rightarrow f\left( {\frac{1}{x}} \right) = \frac{1}{2}\left( {\frac{1}{x} - \frac{1}{x}f\left( x \right)} \right)\]
Khi đó ta có
\[\begin{array}{*{20}{l}}{2f\left( x \right) + \frac{1}{2}x\left( {\frac{1}{x} - \frac{1}{x}f\left( x \right)} \right) = x}\\{ \Leftrightarrow 2f\left( x \right) + \frac{1}{2} - \frac{1}{2}f\left( x \right) = x}\\{ \Leftrightarrow \frac{3}{2}f\left( x \right) = x - \frac{1}{2}}\\{ \Leftrightarrow \frac{3}{2}\mathop \smallint \limits_{\frac{1}{2}}^2 f\left( x \right)dx = \mathop \smallint \limits_{\frac{1}{2}}^2 \left( {x - \frac{1}{2}} \right)dx}\\{ \Leftrightarrow \frac{3}{2}\mathop \smallint \limits_{\frac{1}{2}}^2 f\left( x \right)dx = \frac{9}{8} \Leftrightarrow \mathop \smallint \limits_{\frac{1}{2}}^2 f\left( x \right)dx = \frac{3}{4}}\end{array}\]
Đáp án cần chọn là: D
Câu 22:
Tích phân \[I = \mathop \smallint \limits_2^5 \frac{{dx}}{x}\] có giá trị bằng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 23:
Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn \[[0;\pi ]\]đạt giá trị bằng 0 ?
 Xem đáp án
Xem đáp án
Tính tích phân cho từng hàm số trong các đáp án:
+)\(\int\limits_0^\pi {cos3xdx = \frac{1}{3}sin3x} \left| {_0^\pi } \right. = 0\)
+)\(\int\limits_0^\pi {cos3xdx = - \frac{1}{3}sin3x} \left| {_0^\pi } \right. = \frac{2}{3}\)
+)\(\int\limits_0^\pi {cos\left( {\frac{x}{4} + \frac{\pi }{2}} \right)dx = 4sin\left( {\frac{x}{4} + \frac{\pi }{2}} \right)} \left| {_0^\pi } \right. = 2\left( {\sqrt 2 - 2} \right)\)
+)\(\int\limits_0^\pi {cos\left( {\frac{x}{4} + \frac{\pi }{2}} \right)dx = - 4sin\left( {\frac{x}{4} + \frac{\pi }{2}} \right)} \left| {_0^\pi } \right. = 2\sqrt 2 \)
Đáp án cần chọn là: A
Câu 24:
Tích phân \[I = \mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{dx}}{{\sin x}}\] có giá trị bằng
 Xem đáp án
Xem đáp án
Cách 1:
\[\begin{array}{l}I = \mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{dx}}{{\sin x}}\\ = \mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{\left( {co{s^2}\frac{x}{2} + si{n^2}\frac{x}{2}} \right)}}{{2sin\frac{x}{2}cos\frac{x}{2}}}dx\\ = \frac{1}{2}\mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \left( {cot\frac{x}{2} + tan\frac{x}{2}} \right)dx\\ = \left[ {\ln \left| {sin\frac{x}{2}} \right| - \ln \left| {cos\frac{x}{2}} \right|} \right]\left| {_{\frac{\pi }{3}}^{\frac{\pi }{2}}} \right.\\ = \left[ {\ln \frac{{\sqrt 2 }}{2} - \ln \frac{{\sqrt 2 }}{2}} \right] - \left[ {\ln \frac{1}{2} - \ln \frac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 \end{array}\]
Cách 2:
Bước 1: Dùng máy tính như hình dưới, thu được giá trị 0,549306...
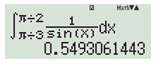
Bước 2: Lấy\[{e^{0,549306...}}\]cho kết quả \[1,732050808... \approx \sqrt 3 \]Chọn\[\frac{1}{2}\ln 3\]
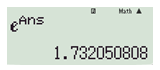
Cách 3:
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng)
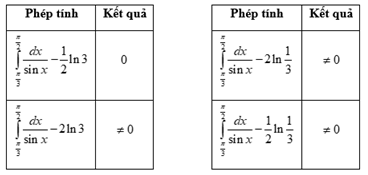
Chọn \[\frac{1}{2}\ln 3\]
Đáp án cần chọn là: C
Câu 25:
Nếu \[\mathop \smallint \limits_{ - 2}^0 \left( {4 - {e^{ - \frac{x}{2}}}} \right)dx = K - 2e\]thì giá trị của K là
 Xem đáp án
Xem đáp án
\[K = \mathop \smallint \limits_{ - 2}^0 \left( {4 - {e^{ - \frac{x}{2}}}} \right)dx + 2e = (4x + 2{e^{ - \frac{x}{2}}})\mid _{ - 2}^0 + 2e = 2 - ( - 8 + 2e) + 2e = 10\]
Đáp án cần chọn là: D
Câu 26:
Tích phân \[I = \mathop \smallint \limits_0^1 \frac{1}{{{x^2} - x - 2}}dx\] có giá trị bằng
 Xem đáp án
Xem đáp án
\(\int\limits_0^1 {\frac{1}{{{x^2} - x - 2}}} dx = \int\limits_0^1 {\frac{1}{{(x - 2)(x + 1)}}} dx = \frac{1}{3}\)
\(\int\limits_0^1 {\left[ {\frac{1}{{x - 2}} - \frac{1}{{x + 1}}} \right]} dx = \frac{1}{3}\left[ {\ln \left| {x - 2} \right| - \ln \left| {x + 1} \right|} \right]\left| {_0^1} \right. = - \frac{{2ln2}}{3}\)
Đáp án cần chọn là: B
Câu 27:
Tích phân \[\mathop \smallint \limits_0^3 x(x - 1)dx\] có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới đây ?
 Xem đáp án
Xem đáp án
Ta có :\(\int\limits_0^3 {x(x - 1)dx = \int\limits_0^3 {({x^2} - x)dx = \frac{{{x^3}}}{3}} } - \frac{{{x^2}}}{2}\left| {_0^3} \right. = 9 - \frac{9}{2} = \frac{9}{2}\)
+)\[\mathop \smallint \limits_0^{\ln \sqrt {10} } {e^{2x}}dx = \frac{{{e^{2x}}}}{2}\left| {_0^{\ln \sqrt {10} }} \right. = \frac{{{e^{2\ln \sqrt {10} }} - 1}}{2} = \frac{9}{2}\]
+)\[3\mathop \smallint \limits_0^{3\pi } \sin xdx = - 3cosx\left| {_0^{3\pi }} \right. = 6\]
+)\[\mathop \smallint \limits_0^2 \left( {{x^2} + x - 3} \right)dx = \left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 3x} \right)\left| {_0^2} \right. = \frac{8}{3} + 2 - 6 = - \frac{4}{3}\]
+)\[\mathop \smallint \limits_0^\pi \cos (3x + \pi )dx = \frac{1}{3}sin(3x + \pi )\left| {_0^\pi } \right. = \frac{1}{3}(sin4\pi - sin\pi ) = 0\]
Đáp án cần chọn là: C
Câu 28:
Cho hai tích phân \[I = \mathop \smallint \limits_0^2 {x^3}dx,J = \int\limits_0^2 {xdx} \]. Tìm mối quan hệ giữa I và J
 Xem đáp án
Xem đáp án
\[I = \mathop \smallint \limits_0^2 {x^3}dx = \frac{{{x^4}}}{4}\left| {_0^2} \right.\]và\[J = \int\limits_0^2 {xdx} = \frac{{{x^2}}}{2}\left| {_0^2} \right. = 2\]
Suy ra\[I.J = 8\]
Đáp án cần chọn là: A
Câu 29:
Tích phân \[I = \mathop \smallint \nolimits_0^{\frac{\pi }{2}} \frac{{4{{\sin }^3}x}}{{1 + \cos x}}dx\] có giá trị bằng
 Xem đáp án
Xem đáp án
\[\frac{{4{{\sin }^3}x}}{{1 + \cos x}} = \frac{{4{{\sin }^3}x(1 - \cos x)}}{{{{\sin }^2}x}} = 4\sin x - 4\sin x\cos x = 4\sin x - 2\sin 2x\]
\[ \Rightarrow I = \mathop \smallint \nolimits_0^{\frac{\pi }{2}} (4\sin x - 2\sin 2x)dx = 2.\]
Đáp án cần chọn là: C
Câu 30:
Tích phân \[I = \mathop \smallint \limits_0^{2\pi } \sqrt {1 + \sin x} dx\] có giá trị bằng
 Xem đáp án
Xem đáp án
Phương pháp tự luận
\[\begin{array}{*{20}{c}}{I = \mathop \smallint \limits_0^{2\pi } \sqrt {{{\left( {\sin \frac{x}{2} + \cos \frac{x}{2}} \right)}^2}} dx = \mathop \smallint \limits_0^{2\pi } \left| {\sin \frac{x}{2} + \cos \frac{x}{2}} \right|dx = \sqrt 2 \mathop \smallint \limits_0^{2\pi } \left| {\sin \left( {\frac{x}{2} + \frac{\pi }{4}} \right)} \right|dx}\\{ = \sqrt 2 \left[ {\mathop \smallint \limits_0^{\frac{{3\pi }}{2}} \sin \left( {\frac{x}{2} + \frac{\pi }{4}} \right)dx - \mathop \smallint \limits_{\frac{{3\pi }}{2}}^{2\pi } \sin \left( {\frac{x}{2} + \frac{\pi }{4}} \right)dx} \right] = 4\sqrt 2 }\end{array}\]
Đáp án cần chọn là: A
Câu 31:
Tích phân \[\mathop \smallint \limits_{ - 1}^5 \left| {{x^2} - 2x - 3} \right|dx\] có giá trị bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 32:
Tích phân \[\mathop \smallint \limits_2^3 \frac{{{x^2} - x + 4}}{{x + 1}}dx\]bằng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 33:
Giá trị của tích phân \[I = \mathop \smallint \limits_0^{\frac{\pi }{2}} \left( {{{\sin }^4}x + {{\cos }^4}x} \right)\left( {{{\sin }^6}x + {{\cos }^6}x} \right)dx\] là:
 Xem đáp án
Xem đáp án
Ta có:
\[\left( {{{\sin }^4}x + {{\cos }^4}x} \right)\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\]
\[ = \left[ {{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right)}^2} - 2{{\sin }^2}x{{\cos }^2}x} \right]\]
\[\left[ {{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right)}^3} - 3{{\sin }^2}x{{\cos }^2}x\left( {{{\sin }^2}x + {{\cos }^2}x} \right)} \right]\]
\[ = \left( {1 - \frac{1}{2}{{\sin }^2}2x} \right)\left( {1 - \frac{3}{4}{{\sin }^2}2x} \right) = 1 - \frac{5}{4}{\sin ^2}2x + \frac{3}{8}{\left( {{{\sin }^2}2x} \right)^2}\]
\[ = 1 - \frac{5}{4}.\frac{{1 - \cos 4x}}{2} + \frac{3}{8}.{\left( {\frac{{1 - \cos 4x}}{2}} \right)^2}\]
\[ = \frac{3}{8} + \frac{5}{8}\cos 4x + \frac{3}{{32}}\left( {1 - 2\cos 4x + {{\cos }^2}4x} \right) = \frac{{15}}{{32}} + \frac{7}{{16}}\cos 4x + \frac{3}{{32}}{\cos ^2}4x\]
\[ = \frac{{15}}{{32}} + \frac{7}{{16}}\cos 4x + \frac{3}{{32}}.\frac{{1 + \cos 8x}}{2} = \frac{{33}}{{64}} + \frac{7}{{16}}\cos 4x + \frac{3}{{64}}\cos 8x\]
Do đó\[I = \mathop \smallint \limits_0^{\frac{\pi }{2}} \left( {\frac{{33}}{{64}} + \frac{7}{{16}}\cos 4x + \frac{3}{{64}}\cos 8x} \right)dx\]
\[ = \frac{{33}}{{64}}x\left| {_0^{\frac{\pi }{2}}} \right. + \frac{7}{{64}}sin4x\left| {_0^{\frac{\pi }{2}}} \right. + \frac{3}{{512}}sin8x\left| {_0^{\frac{\pi }{2}}} \right. = = \frac{{33}}{{128}}\pi \]
Đáp án cần chọn là: B
Câu 34:
Giá trị của a để đẳng thức \[\mathop \smallint \limits_1^2 \left[ {{a^2} + (4 - 4a)x + 4{x^3}} \right]dx = \mathop \smallint \limits_2^4 2xdx\] là đẳng thức đúng
 Xem đáp án
Xem đáp án
Ta có: \(\int\limits_2^4 {2xdx = {x^2}} \left| {_2^4} \right. = 12\)
\(\int\limits_1^2 {[{a^2} + (4 - 4a)x + 4{x^3}]dx} = [{a^2}x + (2 - 2a){x^2} + {x^4}]\left| {_1^2} \right. = {a^2} - 6a + 21\)
\[ \Rightarrow {a^2} - 6a + 21 = 12 \Leftrightarrow a = 3.\]
Đáp án cần chọn là: B
Câu 35:
Biết rằng \[\mathop \smallint \limits_0^{\frac{\pi }{4}} \frac{{\cos 2x}}{{{{\left( {\sin x - \cos x + 3} \right)}^2}}}dx = a + \ln b\] với a,b là các số hữu tỉ. Giá trị của 2a+3b bằng
 Xem đáp án
Xem đáp án
Ta có
\[I = \mathop \smallint \limits_0^{\frac{\pi }{4}} \frac{{\cos 2x}}{{{{\left( {\sin x - \cos x + 3} \right)}^2}}}dx = \mathop \smallint \limits_0^{\frac{\pi }{4}} \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\left( {\sin x - \cos x + 3} \right)}^2}}}dx = \mathop \smallint \limits_0^{\frac{\pi }{4}} \frac{{\left( {\cos x - \sin x} \right)\left( {\cos x + \sin x} \right)}}{{{{\left( {\sin x - \cos x + 3} \right)}^2}}}dx\]
Đặt\[sinx - cosx + 3 = t \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(cosx + sinx)dx = dt}\\{cosx - sinx = 3 - t}\end{array}} \right.\]
Đổi cận\[x = 0 \Rightarrow t = 2;\,x = \frac{\pi }{4} \Rightarrow t = 3\]
Suy ra
\(I = \int\limits_2^3 {\frac{{(3 - t)dt}}{{{t^2}}}} = \int\limits_2^3 {\left( {\frac{3}{{{t^2}}} - \frac{1}{t}} \right)} dt = \left( { - \frac{3}{t} - \ln \left| t \right|} \right)\left| {_2^3} \right. = \frac{1}{2} + ln2 - ln3 = \frac{1}{2} + ln\frac{2}{3}\)
Hay \[a = \frac{1}{2};b = \frac{2}{3} \Rightarrow 2a + 3b = 3.\]
Đáp án cần chọn là: A
Câu 36:
Cho hàm số f(x) có f(0)=0 và \[f\prime (x) = si{n^4}x\forall x \in \mathbb{R}\]. Tích phân \[\mathop \smallint \limits_0^{\frac{\pi }{2}} f\left( x \right)dx\] bằng:
 Xem đáp án
Xem đáp án
Ta có\[f\left( x \right) = \smallint f'\left( x \right)dx = \smallint {\sin ^4}xdx\]
\[\begin{array}{*{20}{l}}{ = \smallint {{\left( {\frac{{1 - \cos 2x}}{2}} \right)}^2}dx}\\{ = \frac{1}{4}\smallint \left( {1 - 2\cos 2x + {{\cos }^2}2x} \right)dx}\\{ = \frac{1}{4}\smallint \left( {1 - 2\cos 2x + \frac{{1 + \cos 4x}}{2}} \right)dx}\\{ = \frac{1}{4}\left( {x - \sin 2x + \frac{1}{2}x + \frac{1}{2}.\frac{{\sin 4x}}{4}} \right) + C}\\{ = \frac{{3x}}{8} - \frac{{\sin 2x}}{4} + \frac{{\sin 4x}}{{32}} + C}\end{array}\]
Theo bài ra ta có\[f\left( 0 \right) = 0 \Leftrightarrow C = 0 \Rightarrow f\left( x \right) = \frac{{3x}}{8} - \frac{{\sin 2x}}{4} + \frac{{\sin 4x}}{{32}}\]
Vậy\[\mathop \smallint \limits_0^{\frac{\pi }{2}} f\left( x \right)dx = \mathop \smallint \limits_0^{\frac{\pi }{2}} \left( {\frac{{3x}}{8} - \frac{{\sin 2x}}{4} + \frac{{\sin 4x}}{{32}}} \right)dx = \frac{{3{\pi ^2} - 16}}{{64}}\] (sử dụng MTCT).
Đáp án cần chọn là: C
Câu 37:
Một ô tô đang đứng và bắt đầu chuyển động theo một đường thẳng với gia tốc \[a\left( t \right) = 6 - 3t\,\,\left( {m/{s^2}} \right)\] trong đó t là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:
 Xem đáp án
Xem đáp án
Ta có\[v\left( t \right) = \smallint a\left( t \right)dt = \smallint \left( {6 - 3t} \right)dt = 6t - \frac{{3{t^2}}}{2} + C\]
Theo bài ra ta có: Ô tô đang đứng yên và bắt đầu chuyển động, do đó\[v\left( 0 \right) = 0\]
\[ \Rightarrow C = 0\]
Khi đó ta có\[v\left( t \right) = 6t - \frac{3}{2}{t^2}\] đây là một parabol có bề lõm hướng xuống, đạt giá trị lớn nhất tại\[t = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.\left( { - \frac{3}{2}} \right)}} = 2\]
Vậy quãng đường ô tô đi được từ khi chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:\[S = \mathop \smallint \limits_0^2 v\left( t \right)dt = \mathop \smallint \limits_0^2 \left( {6t - \frac{3}{2}{t^2}} \right)dt = 8\,\,\left( m \right).\]
Đáp án cần chọn là: D
Câu 38:
Giá trị của tích phân \[\mathop \smallint \limits_0^{2017\pi } \sqrt {1 - \cos 2x} dx\] là
 Xem đáp án
Xem đáp án
Do hàm số\[f(x) = \sqrt {1 - \cos 2x} = \sqrt 2 \left| {\sin x} \right|\] là hàm liên tục và tuần hoàn với chu kì\[T = \pi \] nên ta có
\[\int\limits_0^T {f(x)dx = } \int\limits_T^{2T} {f(x)dx = } \int\limits_{2T}^{3T} {f(x)dx = ... = \int\limits_{(n - 1)T}^{nT} {f(x)dx} } \]
\( \Rightarrow \int\limits_0^{nT} {f(x)dx = } \int\limits_0^T {f(x)dx + \int\limits_T^{2T} {f(x)dx + \int\limits_{2T}^{3T} {f(x)dx + ... + \int\limits_{(n - 1)T}^{nT} {f(x)dx} = } } } n\int\limits_0^T {f(x)dx} \)
\( \Rightarrow \int\limits_0^{2017\pi } {\sqrt {1 - cos2x} } dx\)
\( = 2017\int\limits_0^\pi {\sqrt {1 - cos2x} } dx\)
\( = 2017\sqrt 2 \int\limits_0^\pi {sinxdx = 4034\sqrt 2 } \)
Đáp án cần chọn là: D
Câu 39:
Tìm hai số thực A,B sao cho \[f(x) = Asin\pi x + B\], biết rằng \[f\prime \left( 1 \right) = 2\;\] và \[\mathop \smallint \limits_0^2 f(x)dx = 4\].
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{f(x) = A\sin \pi x + B \Rightarrow f'(x) = A\pi \cos \pi x}\\{f'(1) = 2 \Rightarrow A\pi \cos \pi = 2 \Rightarrow A = - \frac{2}{\pi }}\end{array}\]
\[\mathop \smallint \limits_0^2 f(x)dx = 4 \Rightarrow \mathop \smallint \limits_0^2 (A\sin \pi x + B)dx = 4\]
\[ \Rightarrow - \frac{A}{\pi }\cos 2\pi + 2B + \frac{A}{\pi }\cos 0 = 4 \Rightarrow B = 2\]
Đáp án cần chọn là: D
Câu 40:
Cho hàm số y=f(x) nhận giá trị không âm và liên tục trên đoạn \[\left[ {0;1} \right].\;\]Đặt \[g\left( x \right) = 1 + 2\mathop \smallint \limits_0^x f\left( t \right)dt\]. Biết \[g\left( x \right) \ge {\left[ {f\left( x \right)} \right]^3}\] với mọi \[x \in \left[ {0;1} \right].\] Tích phân \[\mathop \smallint \limits_0^1 \sqrt[3]{{{{\left[ {g\left( x \right)} \right]}^2}}}\,dx\]có giá trị lớn nhất bằng
 Xem đáp án
Xem đáp án
Ta có\[g\left( x \right) = 1 + 2\mathop \smallint \limits_0^x f\left( t \right)dt\]suy ra\(\left\{ {\begin{array}{*{20}{c}}{g(x) - 1 = 2\int\limits_0^2 {f(t)dt} }\\{g(0) = 1 + \int\limits_0^0 {f(t)dt} }\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{g\prime (x) = 2f(x) \Rightarrow f(x) = \frac{{g\prime (x)}}{2}}\\{g(0) = 1}\end{array}} \right.\)
Mà
\[g\left( x \right) \ge {\left[ {f\left( x \right)} \right]^3} \Leftrightarrow g\left( x \right) \ge {\left[ {\frac{{g'\left( x \right)}}{2}} \right]^3} \Leftrightarrow \sqrt[3]{{g\left( x \right)}} \ge \frac{{g'\left( x \right)}}{2} \Leftrightarrow \frac{{g'\left( x \right)}}{{\sqrt[3]{{g\left( x \right)}}}} \le 2\]
Với\[t \in \left[ {0;1} \right]\]Lấy tích phân hai vế ta được
\(\int\limits_0^t {\frac{{g\prime (x)}}{{\sqrt[3]{{g\left( x \right)}}}}} dx \le \int\limits_0^t {2dx} \)
\(\begin{array}{l} \Leftrightarrow \int\limits_0^t {{{[g(x)]}^{\frac{{ - 1}}{3}}}} d(g(x)) \le 2t\\ \Leftrightarrow 2t \ge 32{[g(x)]^{\frac{2}{3}}}\left| {_0^t} \right.\\ \Leftrightarrow \frac{4}{3}t \ge \sqrt[3]{{{g^2}(t)}} - \sqrt[3]{{{g^2}(0)}}\end{array}\)
Mà\[g\left( 0 \right) = 1\] nên\[\sqrt[3]{{{g^2}\left( t \right)}} \le \frac{4}{3}t + 1 \Rightarrow \sqrt[3]{{{g^2}\left( x \right)}} \le \frac{4}{3}x + 1\]
Từ đó ta có\[\mathop \smallint \limits_0^1 \sqrt[3]{{{g^2}\left( x \right)}}\,dx \le \mathop \smallint \limits_0^1 \left( {\frac{4}{3}x + 1} \right)dx\]
\( \Leftrightarrow \int\limits_0^1 {\sqrt[3]{{{g^2}(x)}}} dx \le \left( {\frac{2}{3}{x^2} + x} \right)\left| {_0^1} \right.\)
\( \Leftrightarrow \int\limits_0^1 {\sqrt[3]{{{g^2}(x)}}} dx \le \frac{5}{2}\)
Hay giá trị lớn nhất cần tìm là\[\frac{5}{3}.\]
Đáp án cần chọn là: B
