Trắc nghiệm Tam giác cân Hình học lớp 7 có đáp án (Vận dụng)
-
2798 lượt thi
-
18 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
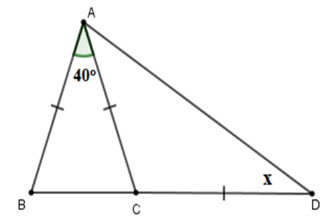
Câu 1: Tính số đo x trên hình vẽ sau:
 Xem đáp án
Xem đáp án
Tam giác ABC cân tại A (vì ) có nên
Mà là góc ngoài của tam giác ACD nên
Lại có: cân tại C (tính chất)
Nên
Vậy
Đáp án cần chọn là C
Câu 2:
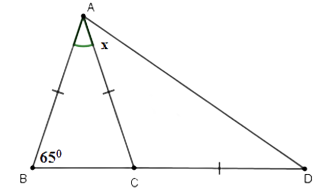
Câu 2: Tính số đo x trên hình vẽ sau:
 Xem đáp án
Xem đáp án
Tam giác ABC cân tại A (vì ) nên
(hai góc kề bù)
Tam giác ACD cân tại D (vì ) và nên
Vậy
Đáp án cần chọn là C
Câu 3:
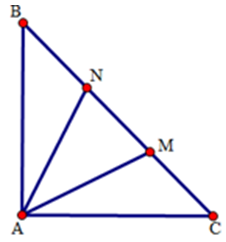
Câu 3.1: Cho tam giác ABC vuông cân ở A. Trên đấy BC lấy hai điểm M, N sao cho . Tam giác AMN là tam giác gì?
 Xem đáp án
Xem đáp án
Do tam giác ABC vuông cân tại A nên
Xét tam giác AMB có , nên tam giác AMB cân ở B
Do đó:
Chứng minh tương tự ta được tam giác ANC cân ở C và
Xét tam giác AMN có , do đó tam giác AMN cân ở A
Đáp án cần chọn là A
Câu 4:
Câu 3: Cho tam giác ABC vuông cân ở A. Trên đấy BC lấy hai điểm M, N sao cho . Tính số đo góc
 Xem đáp án
Xem đáp án
Xét tam giác AMN, ta có:
Vậy
Đáp án cần chọn là A
Câu 5:
Câu 4.1: Cho tam giác ABC vuông cân ở A, có . Trên đáy BC lấy hai điểm M,N sao cho . Tam giác AMN là tam giác gì?
 Xem đáp án
Xem đáp án
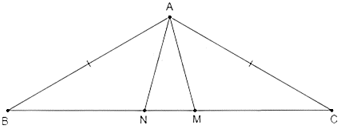
cân ở A nên
Xét có nên cân ở B
Do đó
Chứng minh tương tự ta được tam giác ANC cân ở C và
Xét tam giác AMN có , do đó tam giác AMN cân ở A
Đáp án cần chọn là A
Câu 6:
Câu 4.2: Cho tam giác ABC vuông cân ở A, có . Trên đáy BC lấy hai điểm M,N sao cho . Tính số đo góc
 Xem đáp án
Xem đáp án
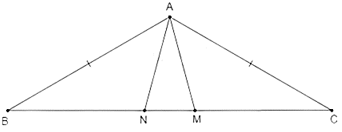
Xét tam giác AMN, ta có:
Vậy
Đáp án cần chọn là B
Câu 7:
Câu 5: Cho tam giác ABC cân tại đỉnh A với . Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho . Phát biểu nào sau đây sai?
 Xem đáp án
Xem đáp án
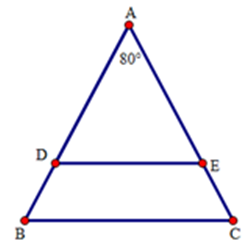
Do tam giác ABC cân nên
Ta thấy tam giác ADE cân do
Do mà hai góc này ở vị trí so le trong nên ED//BC
Vậy đáp án D sai
Đáp án cần chọn là D
Câu 8:
Câu 6: Cho tam giác ABC cân tại đỉnh A với . Kẻ tại D. Trên cạnh AB, lấy điểm E sao cho . Chọn câu sai.
 Xem đáp án
Xem đáp án
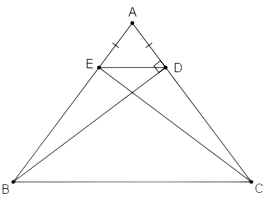
Do tam giác ABC cân nên (1)
Ta thấy có nên cân tại A
(2)
Từ (1) và (2) suy ra . Mà hai góc này ở vị trí đồng vị nên DE//BC
Vậy A đúng
Xét và có
chung
(vì cân tại A)
(hai góc tương ứng )
Do đó là tam giác vuông
Đáp án cần chọn là C
Câu 9:
Câu 7: Cho tam giác ABC có M là trung điểm của BC và . Tính số đo góc BAC là:
 Xem đáp án
Xem đáp án
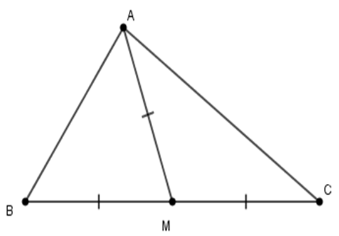
Từ giả thiết suy ra
Ta có: (định lí tổng ba góc trong tam giác ) (1)
Lại có cân tại M (do )
Nên (Tính chất ) (2)
Tương tự cân tại M (do )
Nên (tính chất ) (3)
Từ (1)(2)(3) ta có:
Đáp án cần chọn là C
Câu 10:
Câu 8: Cho tam giác ABC có M là trung điểm của BC và . Chon câu đúng.
 Xem đáp án
Xem đáp án
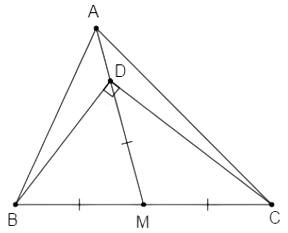
Trên tia MA lấy điểm D sao cho , khi đó D nằm giữa A và M.
Ta có: là góc ngoài đỉnh D của nên suy ra (1)
là góc ngoài đỉnh D của nên suy ra (2)
có (theo cách dựng) nên cân tại M, suy ra
có ( theo cách dựng) nên cân tại M, suy ra
Áp dụng định lí tổng ba góc của một tam giác, ta có:
Từ (1)(2)(3) ta có:
Đáp án cần chọn là C
Câu 11:
Câu 9: Tam giác ABC có . Trên tia đối của tia AC lấy điểm E sao cho . Tính số đo góc CBE.
 Xem đáp án
Xem đáp án
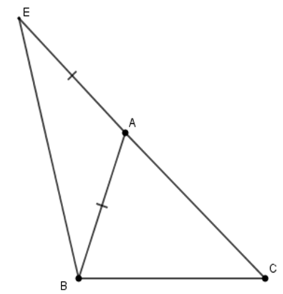
Xét tam giác ABC có (định lí tổng ba góc trong tam giác ) và
Suy ra nên
Xét tam giác AEB cân tại A (do (gt)) nên (tính chất) (1)
Lại có: là góc ngoài tam giác AEB
(2)
Từ (1) và (2) suy ra
Do đó
Đáp án cần chọn là B
Câu 12:
Câu 10: Tam giác ABC có . Trên tia đối của tia AC lấy điểm E sao cho . Tính số đo góc CBE.
 Xem đáp án
Xem đáp án
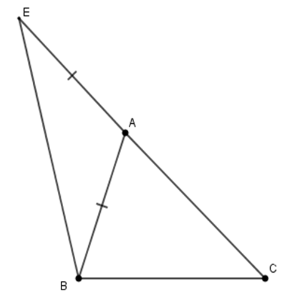
Xét tam giác ABC có (định lí tổng ba góc trong tam giác ) và (gt)
Suy ra nên
Xét tam giác AEB cân tại A (do (gt)) nên (tính chất) (1)
Lại có: là góc ngoài tam giác AEB
(2)
Từ (1) và (2) suy ra
Do đó
Đáp án cần chọn là B
Câu 13:
Câu 11: Cho tam giác ABC có . Trên tia phân giác của góc A lấy điểm D sao cho . Khi đó tam giác BCD là tam giác gì?
 Xem đáp án
Xem đáp án

Lấy sao cho mà nên
cân có nên là tam giác đều suy ra
Thấy (góc ngoài tại đỉnh E của tam giác ABE) nên
Suy ra (hai góc tương ứng bằng nhau) và (hai cạnh tương ứng)
Lại có: nên
cân tại B có nên nó là tam giác đều
Đáp án cần chọn là B
Câu 14:
Câu 12: Cho tam giác ABC có . Vẽ ra phía ngoài của của tam giác hai tam giác đều AMB và ANC
 Xem đáp án
Xem đáp án
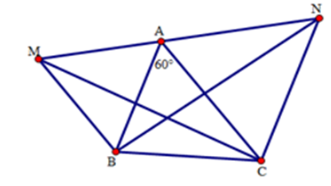
+ Các tam giác AMB và ANC là tam giác đều (gt) nên
Ta có:
Suy ra ba điểm M,A,N thẳng hàng
+ Ta có:
Do đó
Xét hai tam giác ABN và AMC có:
(do tam giác AMB đều)
(cmt)
(do tam giác ANC đều)
(hai cạnh tương ứng)
Vậy cả A,B đều đúng
Đáp án cần chọn là D
Câu 15:
Câu 13: Cho M thuộc đoạn thẳng AB. Trên cùng nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC, BMD. Gọi E,F theo thứ tự là trung điểm của AD,BC. Tam giác MEF là tam giác gì? Chọn câu trả lời đúng nhất.
 Xem đáp án
Xem đáp án
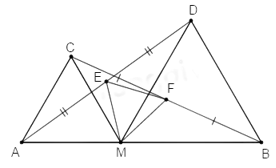
đều nên
đều nên
Từ (1) và (2) suy ra :
Xét và có:
(cmt)
(cmt)
(cmt)
(hai cạnh tương ứng)
(hai góc tương ứng)
Xét và có:
(cmt)
(cmt)
(hai cạnh tương ứng)
(hai góc tương ứng)
Xét tam giác MEF có: (cmt) ; (cmt) nên là tam giác đều
Tam giác đều vừa là tam giác cân vừa là tam giác nhọn(vì có ba góc nhọn) nên cả A,B,C đều đúng
Đáp án cần chọn là D
Câu 16:
Câu 14: Cho tam giác ABC vuông tại A có . Khi đó:
 Xem đáp án
Xem đáp án
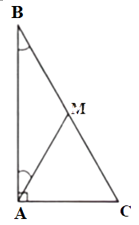
Lấy điểm M trên cạnh BC sao cho
có nên là tam giác cân, suy ra (1)
vuông tại A nên
Ta có:
có nên là tam giác đều, suy ra
Từ (1) và (2) ta có: hay
Đáp án cần chọn là A
Câu 17:
Câu 15: Cho tam giác ABC cân tại A có . Đường vuông góc với AB tại A cắt BC ở D. Độ dài BD bằng:
 Xem đáp án
Xem đáp án
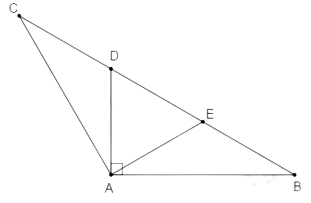
cân tại nên
Ta có:
có nên cân tại D, suy ra (1)
Ta có: là góc ngoài tại đỉnh D của nên
Trên cạnh BD lấy E sao cho thì E nằm giữa B và D
có: nên cân tại E suy ra (2)
Ta có:
có nên là tam giác đều, suy ra (3)
Từ (1),(2),(3) suy ra
Khi đó:
Đáp án cần chọn là C
Câu 18:
Câu 16: Cho tam giác ABC cân tại A có . Về phía ngoài tam giác ABC vẽ tam giác ABD cân tại D có . Tính chu vi tam giác ABD theo a và b.
 Xem đáp án
Xem đáp án
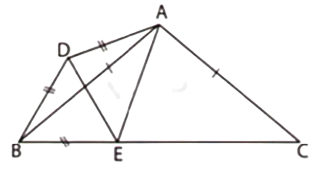
Trên BC lấy điểm E sao cho
cân tại A nên
cân tại D nên
Ta có:
Xét có: nên đều, suy ra
cân tại D (vì (cmt)) nên
có nên cân tại C, suy ra
Do đó :
Vậy chu vi tam giác ABD bằng:
Đáp án cần chọn là C
