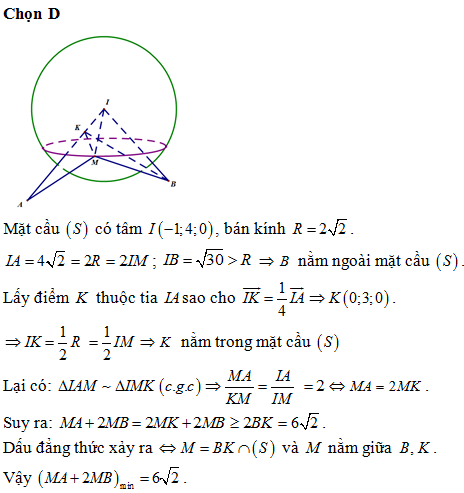
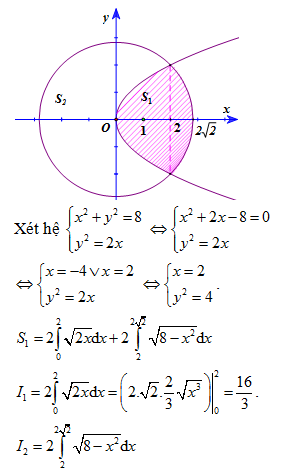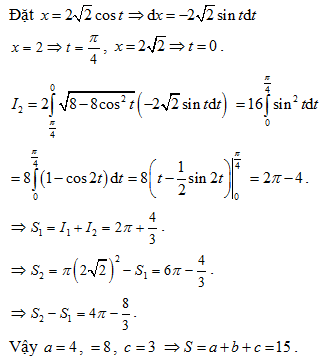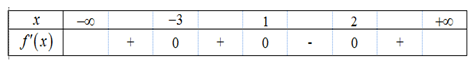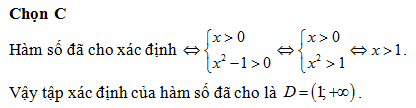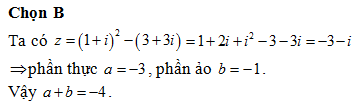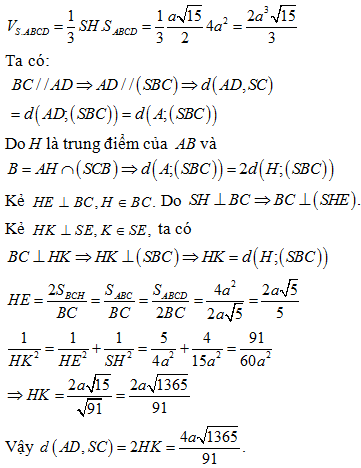Đề thi THPT Quốc gia môn Toán học năm 2022 chọn lọc, có lời giải (30 đề)
Đề thi THPT Quốc gia môn Toán học năm 2022 chọn lọc, có lời giải ( Đề 3)
-
37860 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
Cho dãy số có: . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn C
Sử dụng công thức số hạng tổng quát Ta có: .
Câu 3:
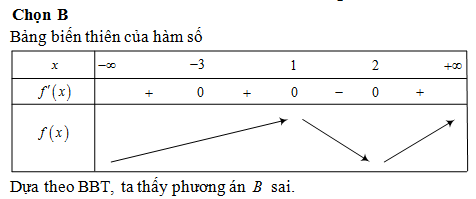
Cho hàm số y =f(x) có bảng biến thiên như sau:
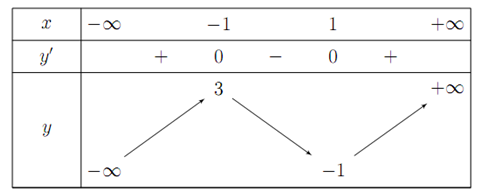
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
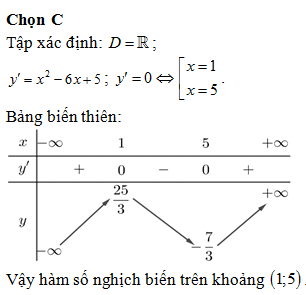
Chọn C
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng .
Câu 4:
Cho hàm số y =f(x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?.
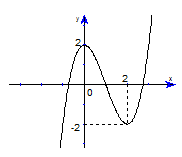
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào đồ thị ta có: Hàm số đạt cực đại tại x=0và đạt cực tiểu tại x=2.
Câu 6:
Cho hàm số . Đường tiệm cận đứng của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Chọn B
Ta có: ; .
Vậy x=1 là đường tiệm cận đứng của đồ thị hàm số.
Câu 7:
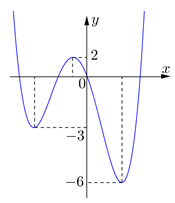
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
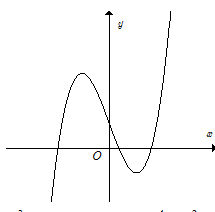
 Xem đáp án
Xem đáp án
Chọn D
Đặc trưng của đồ thị là hàm bậc ba. Loại đáp án A và C.
Khi thì nên chọn D.
Câu 16:
Cho hàm số có một nguyên hàm là F(x). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
Câu 18:
Cho số phức z=2-3i. Số phức liên hợp của số phức z là
 Xem đáp án
Xem đáp án
Chọn B
Số phức liên hợp của số phức là .
Câu 20:
Trong mặt phẳng toạ độ Oxy, tập hợp điểm biểu diễn số phức z có phần thực bằng là đường thẳng có phương trình
 Xem đáp án
Xem đáp án
Tập hợp điểm biểu diễn số phức z có phần thực bằng 3 là đường thẳng x =3.
Chọn D
Câu 21:
Cho hình lăng trụ đứng có diện tích đáy là . Độ dài cạnh bên là . Khi đó thể tích của khối lăng trụ là:
 Xem đáp án
Xem đáp án
Chọn A
Thể tích khối lăng trụ đó là
Câu 23:
Cho khối nón có bán kính và chiều cao h =3. Tính thể tích V của khối nón.
 Xem đáp án
Xem đáp án
Chọn D
Thể tích V của khối nón là : .
Câu 24:
Cho hình trụ có diện tích xung quanh bằng và bán kính đáy bằng a. Độ dài đường sinh của hình trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn C
Câu 28:
Trong không gianOxyz, cho đường thẳng . Vectơ nào dưới đây là một vectơ chỉ phương của d?
 Xem đáp án
Xem đáp án
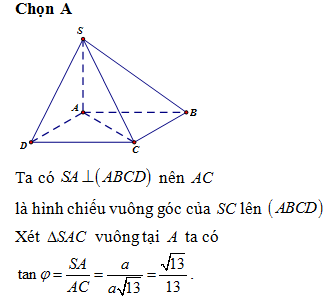
Chọn A
Câu 31:
Giá trị lớn nhất của hàm số trên đoạn [-1;2] có giá trị là một số thuộc khoảng nào dưới đây?
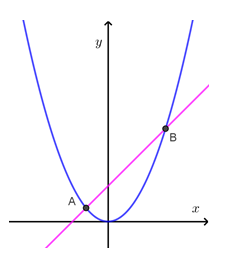
Câu 44:
Biết rằng parabol chia đường tròn thành hai phần lần lượt có diện tích là , (như hình vẽ). Khi đó với a,b,c nguyên dương và là phân số tối giản. Tính S = a+b+c.
 Xem đáp án
Xem đáp án
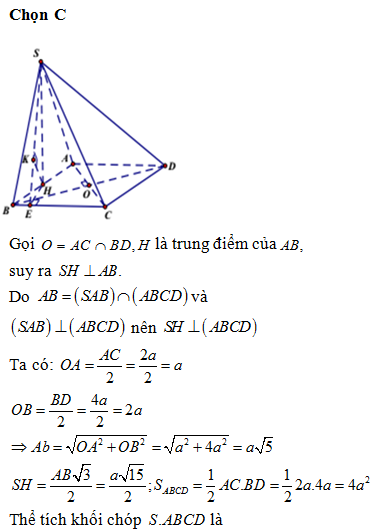
Chọn C