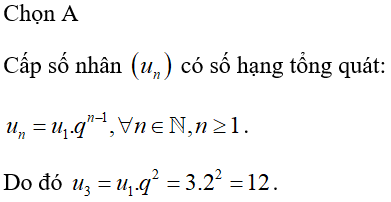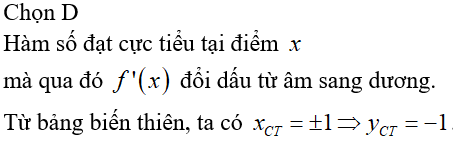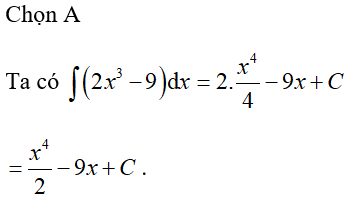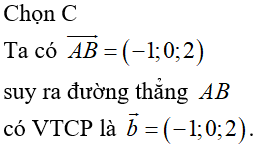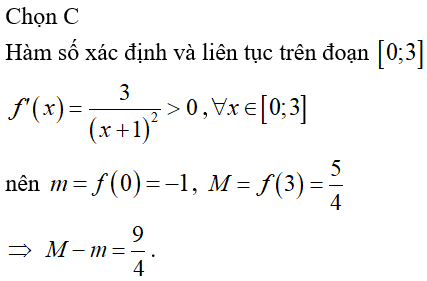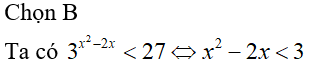50 câu hỏi trắc nghiệm thuộc Đề thi THPT Quốc gia môn Toán học năm 2022 chọn lọc, có lời giải ( Đề 10)

Câu 1:

Có bao nhiêu số có bốn chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5?

$A . A_{5}^{4}$

$B . P_{5}$

$C . C_{5}^{4}$

$D . P_{4}$

Xem đáp án

Chọn A

Số tự nhiên gồm bốn chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5 là một chỉnh hợp chập 4 của 5 phần tử

Vậy có $A_{5}^{4}$ số cần tìm

Câu 2:

Cho cấp số nhân $(u_{n})$ với $u_{1} = 3$ , công bội q=2. Số hạng $u_{3}$ của cấp số nhân đã cho bằng

A. 12

B. 7

C. 24

D. 48

Xem đáp án

Câu 3:

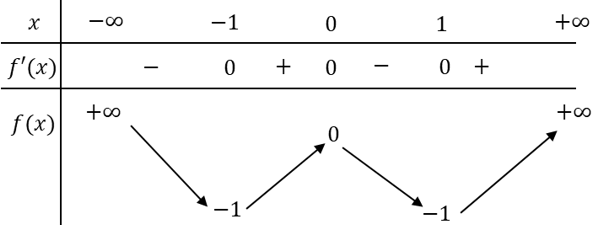
Cho hàm số y=f(x) có bảng biến thiên như sau:

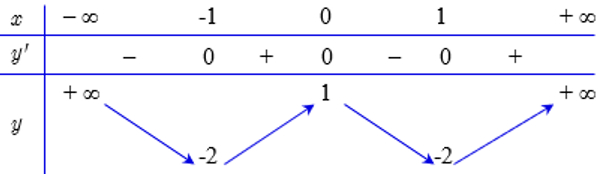
Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?

A. (0;1)

B. (-1;1)

C. (-1;0)

$D . (- \infty; - 1)$

Xem đáp án

Chọn C

Từ bảng biến thiên ta có hàm số đồng biến trên khoảng (-1;0)

Câu 4:

Cho hàm số f(x) có bảng biến thiên như sau:

Hàm số có cực tiểu là

A. x=-1

B. x=1

C. y=3

D. y=-1

Xem đáp án

Câu 5:

Cho hàm số f(x) có bảng biến thiên như sau:

Hỏi hàm số có bao nhiêu điểm cực trị?

A. 4

B. 3

C. 5

D. 2

Xem đáp án

Câu 6:

Đồ thị hàm số $y = \frac{\sqrt{2}}{x + 1}$ có đường tiệm cận đứng là

A. x=1

B. y=-1

C. x=-1

$D . x = \sqrt{2}$

Xem đáp án

Câu 7:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

$A . y = - x^{3} + 2 x^{2} - 1$

$B . y = x^{4} - 3 x^{2} + 1$

$C . y = - x^{4} + 3 x^{2} - 1$

$D . y = \frac{x + 1}{2 x - 1}$

Xem đáp án

Câu 8:

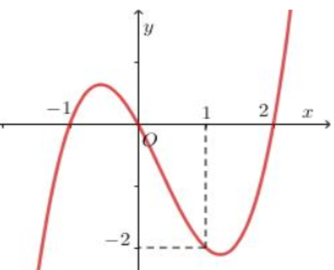
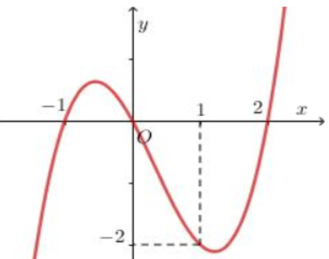
Đồ thị $y = x^{4} - 3 x^{2} + 2$ cắt trục tung tại điểm có tung độ bằng

$A . \sqrt{2}$

B. -1

C. 1

D. 2

Xem đáp án

Chọn A

Cắt trục tung suy ra x=0 do đó đồ thị cắt trục tung tại điểm y=2

Câu 9:

Với a là số thực dương tùy ý, $\log_{2} a^{2}$ bằng:

$A . 2 + \log_{2} a$

$B . \frac{1}{2} + \log_{2} a$

$C . 2 \log_{2} a$

$D . \frac{1}{2} \log_{2} a$

Xem đáp án

Câu 10:

Với a là số thực dương tùy ý, $P = \sqrt[3]{a . \sqrt[4]{a}}$ bằng

$A . P = a^{\frac{5}{4}}$

$B . P = a^{\frac{5}{12}}$

$C . P = a^{\frac{1}{7}}$

$D . P = a^{\frac{1}{12}}$

Xem đáp án

Câu 11:

Đạo hàm của hàm số $y = 3^{x}$ là

$A . y' = 3^{x} \ln 3$

$B . y' = 3^{x}$

$C . y' = \frac{3^{x}}{\ln 3}$

$D . y' = x 3^{x - 1}$

Xem đáp án

Câu 12:

Số nghiệm của phương trình $2^{2 x^{2} - 5 x + 3}$ =1 là:

A. 3

B. 2

C. 0

D. 1

Xem đáp án

Câu 13:

Tìm các nghiệm của phương trình $\log_{3} (2 x - 3) = 2$

$A . x = \frac{11}{2}$

$B . x = \frac{9}{2}$

C. x=6

D. x=5

Xem đáp án

Câu 14:

Cho hàm của hàm số $f (x) = 2 x^{3} - 9$ . Trong các khẳng định sau, khẳng định nào đúng?

$A . \int f (x) d x = \frac{1}{2} x^{4} - 9 x + C$

$B . \int f (x) d x = 4 x^{4} - 9 x + C$

$C . \int f (x) d x = \frac{1}{4} x^{4} + C$

$D . \int f (x) d x = 4 x^{3} - 9 x + C$

Xem đáp án

Câu 15:

Cho hàm của hàm số f(x)=sin2x. Trong các khẳng định sau, khẳng định nào đúng?

$A . \int f (x) d x = \frac{1}{2} \cos 2 x + C$

$B . \int f (x) d x = - \frac{1}{2} \cos 2 x$

$C . \int f (x) d x = - c os 2 x + C$

$D . \int f (x) d x = - \frac{1}{2} \cos 2 x + C$

Xem đáp án

Câu 16:

Nếu $\int_{0}^{9} f (x) d x = 37$ và $\int_{9}^{0} g (x) d x = 16$ . thì $I = \int [2 f (x) + 3 g (x)] d x$ bằng

A. I=26

B. I=58

C. I=143

D. I=122

Xem đáp án

Câu 17:

Tích phân $\int_{0}^{2} \frac{2}{2 x + 1} d x$ bằng

A. 2ln5

$B . \frac{1}{2} \ln 5$

C. ln5

D. 4ln5

Xem đáp án

Câu 18:

Tính môđun của số phức z=3+4i.

A. 3

B. 5

C. 7

$D . \sqrt{7}$

Xem đáp án

Câu 19:

Cho hai số phức $z_{1} = 1 - 2 i$ , $z_{2} = - 2 + i$ . Tìm số phức $z = z_{1} z_{2}$

A. z=5i

B. z=-5i

C. z=4-5i

D. z=-4+5i

Xem đáp án

Câu 20:

Cho số phức z=2-3i. Điểm biểu diễn số phức liên hợp của z là

A. (2;3)

B. (-2;-3)

C. (2;-3)

D. (-2;3)

Xem đáp án

Câu 21:

Một khối chóp có diện tích đáy bằng $a^{2}$ và chiều cao bằng $a$ $\sqrt{3}$ . Thể tích của khối chóp đó bằng

$A . \frac{a^{3} \sqrt{3}}{6}$

$B . \frac{a^{3} \sqrt{3}}{3}$

$C . \frac{a^{3}}{4}$

$D . a^{3} \sqrt{3}$

Xem đáp án

Câu 22:

Thể tích khối hộp chữ nhật có ba kích thước lần lượt a; 2a; 3a

$A . V = 6 a^{2}$

$B . V = 2 a^{3}$

$C . V = 6 a^{3}$

$D . V = 3 a^{3}$

Xem đáp án

Câu 23:

Cho hình trụ có bán kính đáy R=8 và độ dài đường sinh l=3. Diện tích xung quanh của hình trụ đã cho bằng:

$A . 24 π$

$B . 192 π$

$C . 48 π$

$D . 64 π$

Xem đáp án

Câu 24:

Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh $S_{x q}$ của hình nón là:

$A . S_{x q} = \frac{1}{3} {πr}^{2} h$

$B . S_{x q} = πr l$

$C . S_{x q} = πrh$

$D . S_{x q} = 2 πr l$

Xem đáp án

Câu 25:

Trong không gian Oxyz, cho điểm A(3;-1;1). Hình chiếu vuông góc của điểm trên mặt phẳng Oyz là điểm

A. M(3;0;0)

B. N(0;-1;1)

C. P(0;-1;0)

D. Q(0;0;1)

Xem đáp án

Chọn B

Khi chiếu vuông góc một điểm trong không gian lên mặt phẳng (Oyz), ta giữ lại các thành phần tung độ và cao độ nên hình chiếu của A(3;-1;1) lên (Oxy) là điểm N(0;-1;1).

Câu 26:

Trong không gian Oxyz, cho mặt cầu (S): ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{3} = 16$ . Tâm của (S) có tọa độ là

A. (-1;-2;-3)

B. (1;2;3)

C. (-1;2;-3)

D. (1;-2;3)

Xem đáp án

Câu 27:

Trong không gian Oxyz, mặt phẳng $(α) : x - 2 y + z - 4 = 0$ đi qua điểm nào sau đây

A. Q(1;-1;1)

B. N(0;2;0)

C. P(0;0;-4)

D. M(1;0;0)

Xem đáp án

Câu 28:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;1;0) và B(0;1;2). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng AB.

$A . \vec{d} = (- 1; 1; 2)$

$B . \vec{a} = (- 1; 0; - 2)$

$C . \vec{b} = (- 1; 0; 2)$

$D . \vec{c} = (1; 2; 2)$

Xem đáp án

Câu 29:

Cho tập A= $\{1; 2; 4; 5; 6\}$ , gọi S là tập các số tự nhiên có 3 chữ số đôi một khác nhau tạo thành từ A lấy ngẫu nhiên một phần tử của S.Tính xác suất số đó là lẻ.

$A . \frac{1}{3}$

$B . \frac{2}{3}$

$C . \frac{3}{5}$

$D . \frac{2}{5}$

Xem đáp án

Câu 30:

Hàm số nào dưới đây đồng biến trên khoảng $(- \infty; + \infty)$

A. y=-2x+1

$B . y = x^{3} + x - 2$

$C . y = - x^{4} + 2 x^{2} + 1$

$D . y = \frac{x - 1}{x + 1}$

Xem đáp án

Câu 31:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = \frac{2 x - 1}{x + 1}$ trên đoạn [0;3]. Tính hiệu M-m.

$A . M - m = - \frac{9}{4}$

B. M-m=3

$C . M - m = \frac{9}{4}$

$D . M - m = \frac{1}{4}$

Xem đáp án

Câu 32:

Giải bất phương trình $3^{x^{2} - 2 x} < 27$

$A . (3; + \infty)$

B. (-1;3)

$C . (- \infty; 1) \cup (3; + \infty)$

$D . (- \infty; 1)$

Xem đáp án

Câu 33:

Cho $\int_{1}^{2} [4 f (x) - 2 x] d x = 1$ . Khi đó $\int_{1}^{2} f (x) d x$ bằng:

A. 1

B. -3

C. 3

D. -1

Xem đáp án

Câu 34:

Cho số phức z=2-i, số phức $(2 - 3 i) \bar{z}$ bằng

A. -1+8i

B. -7+4i

C. 7-4i

D. 1+8i

Xem đáp án

Câu 35:

Cho hình hộp chữ nhật ABCD.A'B'C'D', biết đáy ABCD là hình vuông. Tính góc giữa A'C và BD

$A . 90^{°}$

$B . 30^{°}$

$C . 60^{°}$

$D . 45^{°}$

Xem đáp án

Câu 36:

Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (BCD)

$A . \frac{a \sqrt{6}}{2}$

$B . \frac{a \sqrt{6}}{3}$

$C . \frac{3 a}{2}$

D. 2a

Xem đáp án

Câu 37:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0;0;-3) và đi qua điểm M(4;0;0). Phương trình của (S) là

$A . x^{2} + y^{2} + {(z + 3)}^{2} = 25$

$B . x^{2} + y^{2} + {(z + 3)}^{2} = 5$

$C . x^{2} + y^{2} + {(z - 3)}^{2} = 25$

$D . x^{2} + y^{2} + {(z - 3)}^{2} = 5$

Xem đáp án

Câu 38:

Trong không gian Oxyz, cho hai điểm M(1;0;1) và N(3;2;-1). Đường thẳng MN có phương trình tham số là

$A . \{\begin{cases} x = 1 + 2 t \\ y = 2 t \\ z = 1 + t \end{cases}$

$B . \{\begin{cases} x = 1 + t \\ y = t \\ z = 1 + t \end{cases}$

$C . \{\begin{cases} x = 1 - t \\ y = t \\ z = 1 + t \end{cases}$

$D . \{\begin{cases} x = 1 + t \\ y = t \\ z = 1 - t \end{cases}$

Xem đáp án

Câu 39:

Cho hàm số y=f(x) liên tục trên R, hàm số f'(x) có đồ thị như hình vẽ bên dưới.

Hàm số $g (x) = 3 f (x^{2} - 2) - \frac{3}{2} x^{4} - 3 x^{2} + 2$ đạt giá trị lớn nhất trên [-2;2] bằng

A. g(1)

B. g(-2)

C. g(0)

D. g(2)

Xem đáp án

Câu 40:

Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện: $3^{|x^{2} - 2 x - 3| - \log_{3} 5} = 5^{- (y + 4)}$ và $4 |y| - |y - 1| + {(y + 3)}^{2} \leq 8$

A. 3

B. 2

C. 1

D. 4

Xem đáp án

Chọn B

*) $5^{- (y + 4)} = 3^{|x^{2} - 2 x - 3| - \log_{3} 5} \geq 3^{- \log_{3} 5} \Rightarrow 5^{- (y + 4)} \geq 5^{- 1} \Rightarrow - (y + 4) \geq - 1 \Rightarrow y \leq - 3$ dấu bằng khi $|x^{2} - 2 x - 3| = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 3 \end{array}$ .

*) Khi đó $4 |y| - |y - 1| + {(y + 3)}^{2} \leq 8 \Leftrightarrow - 4 y - (1 - y) + y^{2} + 6 y + 9 \leq 8 \Leftrightarrow y^{2} + 3 y \leq 0 \Leftrightarrow - 3 \leq y \leq 0$ .

Kết hợp với điều kiện trên $y \leq 0 \Rightarrow y = - 3$ . Với y=-3. Ta có $[\begin{array}{l} x = - 1 \\ x = 3 \end{array}$ .

Vậy có hai cặp số thỏa mãn $\{\begin{cases} x = - 1 \\ y = - 3 \end{cases}; \{\begin{cases} x = 3 \\ y = - 3 \end{cases}$ .

Câu 41:

Có bao nhiêu số phức z thỏa mãn $|(1 + 3 i) z - 16 - 28 i| = 20$ và $(z - 4 - 2 i) (\bar{z} + 2)$ là số thuần ảo?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Chọn B.

 $|(1 + 3 i) z - 16 - 28 i| = 20 \Leftrightarrow \frac{|(1 + 3 i) z - 16 - 28 i|}{|(1 + 3 i)|} = \frac{20}{|(1 + 3 i)|} \Leftrightarrow |z - 10 + 2 i| = 2 \sqrt{10}$

$\Rightarrow$ Số phức z thuộc đường tròn tâm I(10;-2), bán kính $R = 2 \sqrt{10}$

 Gọi z=a+bi.

$(z - 4 - 2 i) (\bar{z} + 2)$ là số thuần ảo $\Leftrightarrow a^{2} + b^{2} - 2 a - 2 b - 8 = 0$

$\Rightarrow$ Số phức z thuộc đường tròn tâm $I_{1} (1; 1)$ , bán kính $R_{1} = \sqrt{10}$

 Ta có $I I_{1} = 3 \sqrt{10} = R + R_{1} \Rightarrow$ đường tròn tâm $I_{1}$ và đường tròn tâm I tiếp xúc ngoài.

Nên có 1 số phức z thỏa mãn thỏa mãn yêu cầu bài toán.

Câu 42:

Cho hình chóp đều S.ABCD có cạnh bên bằng $a \sqrt{3}$ , mặt bên tạo với đáy một góc $45^{°}$

Thể tích khối chóp S.ABC bằng

$A . V = \frac{3 \sqrt{6} a^{3}}{4}$

$B . V = \frac{3 \sqrt{6} a^{3}}{2}$

$C . \frac{2 a^{3}}{3}$

$D . \frac{4 a^{3}}{3}$

Xem đáp án

Câu 43:

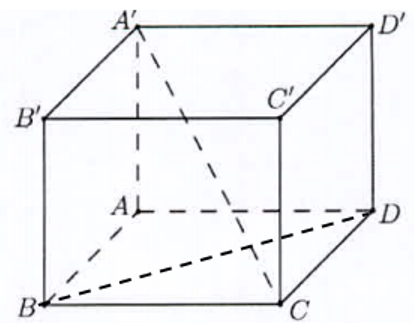
Từ một khối gỗ hình trụ có chiều cao bằng 60cm người ta đẽo được một khối lăng trụ đứng ABC.A'B'C' có hai đáy là hai tam giác nội tiếp hai đáy hình trụ và $A B = 6 c m; A C = 18 c m, \hat{B A C} = 120^{0}$ . Tính thể tích lượng gỗ bỏ đi khi đẽo khúc gỗ thành khối lăng trụ đó (làm tròn đến hàng phần trăm).

$A . 26 599, 38 c m^{3}$

$B . 25 699, 38 c m^{3}$

$C . 28469, 99 c m^{3}$

$D . 28470, 00 c m^{3}$

Xem đáp án

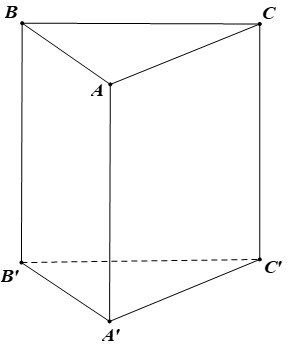
Chọn A

Áp dụng định lý cosin cho tam giác ABC ta có:

$B C = \sqrt{A B^{2} + A C^{2} - 2. A B . A C . \cos \hat{B A C}} = \sqrt{6^{2} + 18^{2} - 2.6.18. \cos 120^{0}} = 6 \sqrt{13}$ .

Áp dụng định lý sin cho tam giác ABC ta có: $\frac{B C}{\sin \hat{B A C}} = 2 R \Rightarrow R = \frac{B C}{2 \sin \hat{B A C}} = \frac{6 \sqrt{13}}{2 \sin 120^{0}} = 2 \sqrt{39}$ .

Thể tích của khối trụ có 2 đáy ngoại tiếp hai đáy khối lăng trụ là: $V_{1} = π R^{2} h = π . {(2 \sqrt{39})}^{2} .60 = 9360 π$ .

Thể tích của khối lăng trụ là:

$V_{2} = S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin 120^{0} . = \frac{1}{2} .6.18.60. \sin 120^{0} = 1620 \sqrt{3}$ .

Tính thể tích lượng gỗ bỏ đi là: $V = V_{1} - V_{2} = 9360 π - 1620 \sqrt{3} = 2659, 38493 \approx 2659, 38 c m^{3}$ .

Câu 44:

Trong không gian Oxyz cho hai đường thẳng chéo nhau $d_{1} : \frac{x - 2}{1} = \frac{y + 3}{2} = \frac{z - 3}{- 1}$ , $d_{2} : \frac{x - 1}{2} = \frac{y - 1}{1} = \frac{z - 4}{1}$ . Đường vuông góc chung của hai đường thẳng $d_{1}, d_{2}$ có phương trình là

$A . \frac{x - 3}{1} = \frac{y + 1}{- 1} = \frac{z - 2}{- 1}$

$B . \frac{x - 3}{1} = \frac{y - 1}{1} = \frac{z - 2}{- 1}$

$C . \frac{x - 1}{1} = \frac{y - 1}{1} = \frac{z - 4}{- 1}$

$D . \frac{x + 1}{1} = \frac{y + 1}{- 1} = \frac{z + 4}{- 1}$

Xem đáp án

Chọn A

Gọi $Δ$ là đường vuông góc chung của hai đường thẳng $d_{1}, d_{2}$ và A,B lần lượt là giao điểm của $Δ$ và $d_{1}, d_{2}$

Khi đó ta có $A (2 + t; - 3 + 2 t; 3 - t); B (1 + t^{'}; 1 + t^{'}; 4 + t^{'}) \Rightarrow \vec{A B} (- 1 + t^{'} - t; 4 + t^{'} - 2 t; 1 + t^{'} + t)$

Gọi $\vec{u_{1}} (1; 2; - 1), \vec{u_{2}} (2; 1; 1)$ lần lượt là VTCP của $d_{1}, d_{2}$

Ta có $\{\begin{cases} Δ ⊥ d_{1} \\ Δ ⊥ d_{2} \end{cases} \Rightarrow \{\begin{cases} \vec{A B} . \vec{u_{1}} = 0 \\ \vec{A B} . \vec{u_{2}} = 0 \end{cases} \Leftrightarrow \{\begin{cases} - 1 + t^{'} - t + 8 + 2 t^{'} - 4 t - 1 - t^{'} - t = 0 \\ - 2 + 2 t^{'} - 2 t + 4 + t^{'} - 2 t + 1 + t^{'} + t = 0 \end{cases} \Leftrightarrow \{\begin{cases} t = 1 \\ t^{'} = 0 \end{cases}$

$\Rightarrow A (3; - 1; 2); \vec{A B} (- 2; 2; 2)$

Vậy đường thẳng $Δ$ đi qua A và có VTCP $\vec{u} = - \frac{1}{2} \vec{A B}$ có phương trình chính tắc là: $\frac{x - 3}{1} = \frac{y + 1}{- 1} = \frac{z - 2}{- 1}$ .

Câu 45:

Cho hàm số $f (x) = \{\begin{cases} x^{2} + 1, x \geq 1 \\ 2 x, x < 1 \end{cases}$ . Tích phân $\int_{0}^{\frac{π}{2}} \sin x . \sin 2 x . f (2 \sin^{3} x) d x$ bằng

$A . \frac{13}{9}$

$B . \frac{5}{3}$

C. 3

$D . \frac{13}{3}$

Xem đáp án

Chọn A

Đặt $t = 2 \sin^{3} x$

$\begin{array}{l} \Rightarrow d t = 2.3 \sin^{2} x . \cos x d x \\ \Leftrightarrow d t = 3 \sin 2 x . s i n x d x \end{array}$

$\begin{array}{l} \int_{0}^{\frac{π}{2}} \sin x . \sin 2 x . f (2 \sin^{3} x) d x = \frac{1}{3} \int_{0}^{2} f (t) d t = \frac{1}{3} \int_{0}^{2} f (x) d x \\ = \frac{1}{3} [\int_{0}^{1} f (x) d x + \int_{1}^{2} f (x) d x] = \frac{1}{3} [\int_{0}^{1} (2 x) d x + \int_{1}^{2} (x^{2} + 1) d x] = \frac{13}{9} \end{array}$ .

Câu 46:

Cho hàm số y=f(x) có đạo hàm liên tục trên $ℝ$ . Biết rằng hàm số $y = f (x^{2} - 3 x)$ có đồ thị của đạo hàm như hình vẽ dưới đây

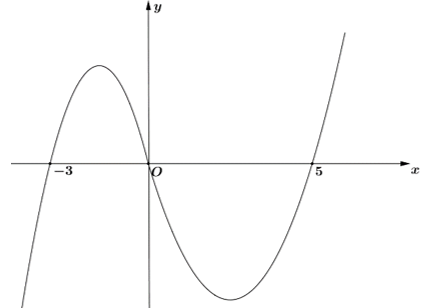
Hàm số $y = f (x^{4} - 8 {|x|}^{3} + 13 x^{2} + 12 |x|)$ có bao nhiêu điểm cực trị

A. 7

B. 13

C. 9

D. 11

Xem đáp án

Chọn D

$y = f (x^{2} - 3 x) \Rightarrow y^{'} = (2 x - 3) f^{'} (x^{2} - 3 x)$ ; $(2 x - 3) f^{'} (x^{2} - 3 x) = 0 \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = 0 \\ x = 5 \end{array}$ .

Đặt $g (x) = f (x^{4} - 8 x^{3} + 13 x^{2} + 12 x) \Rightarrow g (|x|) = f (x^{4} - 8 {|x|}^{3} + 13 x^{2} + 12 |x|)$

$g (x) = f ({(x^{2} - 4 x)}^{2} - 3 (x^{2} - 4 x)) = f (x^{2} - 4 x)$

$g^{'} (x) = (2 x - 4) f^{'} (x^{2} - 4 x)$ ; $g^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x^{2} - 4 x = - 3 \\ x^{2} - 4 x = 0 \\ x^{2} - 4 x = 5 \end{array} \Leftrightarrow x \in \{2; 1; 3; 0; 4; - 1; 5\}$ .

Các nghiệm của g'(x) đều là các nghiệm đơn nên hàm số g(x) có 7 điểm cực trị trong đó có 5 điểm cực trị dương.

Do đó, hàm số $g (|x|)$ có 11 điểm cực trị.

Câu 47:

Gọi S là tập hợp tất cả các số nguyên dương y sao cho tồn tại duy nhất một giá trị của x thỏa mãn $\log_{3} \frac{y \sqrt{x^{2} + 4} + 1}{3 x + 2} + 3 (y \sqrt{x^{2} + 4} - 3 x) = 3$ . Số phần tử của (S) là

A. 0

B. 2

C. 3

D. vô số

Xem đáp án

Chọn B

Điều kiện: $x > - \frac{3}{2}$

$\log_{3} \frac{y \sqrt{x^{2} + 4} + 1}{3 x + 2} + 3 (y \sqrt{x^{2} + 4} - 3 x) = 3$

$\Leftrightarrow \log_{3} (y \sqrt{x^{2} + 4} + 1) - \log_{3} (3 x + 2) + 3 (y \sqrt{x^{2} + 4} - 3 x) = 3$

$\Leftrightarrow \log_{3} (y \sqrt{x^{2} + 4} + 1) + 3 (y \sqrt{x^{2} + 4} + 1) = \log_{3} (3 x + 2) + 3 (3 x + 2)$ (1)

Xét hàm số $f (t) = \log_{3} t + 3 t$ trên $(0; + \infty)$

$f^{'} (t) = \frac{1}{3 \ln t} + 3 > 0, \forall x > 0$ . Suy ra hàm số $f (t) = \log_{3} t + 3 t$ đồng biến trên khoảng $(0; + \infty)$ .

(1) có dạng $f (y \sqrt{x^{2} + 4}) = f (3 x + 2) \Leftrightarrow y \sqrt{x^{2} + 4} = 3 x + 2 \Leftrightarrow y = \frac{3 x + 2}{\sqrt{x^{2} + 4}}$ (1)

Xét hàm số $g (x) = \frac{3 x + 2}{\sqrt{x^{2} + 4}}$ , $g^{'} (x) = \frac{12 - 2 x}{{(\sqrt{4 + x^{2}})}^{3}}$ ; $g^{'} (x) = 0 \Leftrightarrow x = 6$ .

Bảng biến thiên

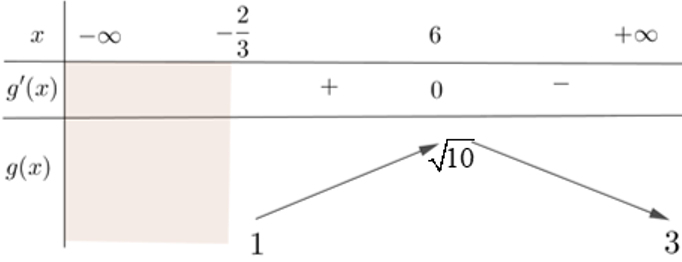
Tồn tại đúng 1 giá trị của x khi phương trình (1) có đúng 1 nghiệm $\Leftrightarrow [\begin{array}{l} 1 < y \leq 3 \\ y = \sqrt{10} \end{array}$ .

Vậy có đúng 2 giá trị nguyên của y thỏa mãn yêu cầu bài toán.

Câu 48:

Cho hàm số $y = x^{4} - 3 x^{2} + m$ có đồ thị $(C_{m})$ , với m là tham số thực. Giả sử $(C_{m})$ cắt trục Ox tại bốn điểm phân biệt như hình vẽ

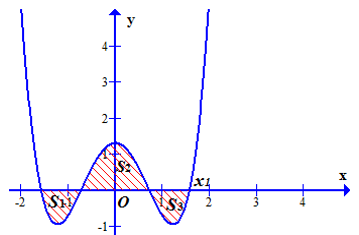
Gọi $S_{1}$ , $S_{2}$ , $S_{3}$ là diện tích các miền gạch chéo được cho trên hình vẽ. Giả sử $m = \frac{a}{b}$ ( $\frac{a}{b}$ là phân số tối giản, a>0) để $S_{1} + S_{3} = S_{2}$ . Giá trị của biểu thức T=3a+2b là

A. 4

B. 22

C. 3

D. 23

Xem đáp án

Chọn B

Gọi $x_{1}$ là nghiệm dương lớn nhất của phương trình $x^{4} - 3 x^{2} + m = 0$ , ta có $m = - x_{1}^{4} + 3 x_{1}^{2} (1)$ .

Vì $S_{1} + S_{3} = S_{2}$ và $S_{1} = S_{3}$ nên $S_{2} = 2 S_{3}$ hay $\int_{0}^{x_{1}} f (x) d x = 0$ .

Mà $\int_{0}^{x_{1}} f (x) d x = \int_{0}^{x_{1}} (x^{4} - 3 x^{2} + m) d x = {(\frac{x^{5}}{5} - x^{3} + m x)|}_{0}^{x_{1}} = \frac{x_{1}^{5}}{5} - x_{1}^{3} + m x_{1} = x_{1} (\frac{x_{1}^{4}}{5} - x_{1}^{2} + m)$ .

Do đó, $x_{1} (\frac{x_{1}^{4}}{5} - x_{1}^{2} + m) = 0 \Leftrightarrow \frac{x_{1}^{4}}{5} - x_{1}^{2} + m = 0$ (2).

Từ (1) và (2), ta có phương trình $\frac{x_{1}^{4}}{5} - x_{1}^{2} - x_{1}^{4} + 3 x_{1}^{2} = 0 \Leftrightarrow - 4 x_{1}^{4} + 10 x_{1}^{2} = 0 \Leftrightarrow x_{1}^{2} = \frac{5}{2}$ .

Vậy $m = - x_{1}^{4} + 3 x_{1}^{2} = \frac{5}{4}$ .

Câu 49:

Cho $z_{1}, z_{2}$ là các số phức thỏa mãn $|{\bar{z}}_{1} - 3 + 2 i| = |{\bar{z}}_{2} - 3 + 2 i| = 2$ và $|z_{1} - z_{2}| = 2 \sqrt{3}$ . Gọi m,n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z_{1} + z_{2} - 3 - 5 i|$ . Giá trị của biểu thức T=m+2n bằng

$A . T = 3 \sqrt{10} - 2$

$B . T = 6 - \sqrt{10}$

$C . 6 - \sqrt{34}$

$D . 3 \sqrt{34} - 2$

Xem đáp án

Chọn A

$\{\begin{cases} |{\bar{z}}_{1} - 3 + 2 i| = 2 \\ |{\bar{z}}_{2} - 3 + 2 i| = 2 \\ |z_{1} - z_{2}| = 2 \sqrt{3} \end{cases} \Leftrightarrow \{\begin{cases} |z_{1} - 3 - 2 i| = 2 \\ |z_{2} - 3 - 2 i| = 2 \\ |z_{1} - z_{2}| = 2 \sqrt{3} \end{cases}$

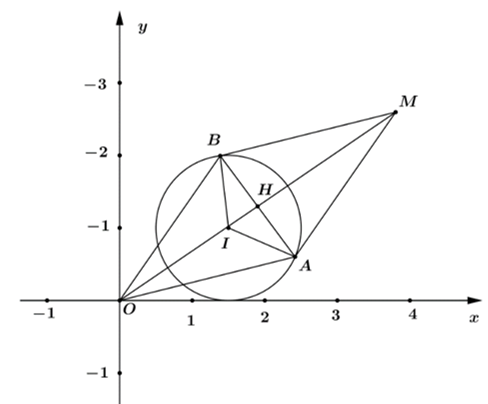
Gọi A,B,I lần lượt là các điểm biểu diễn cho số phức $z_{1}, z_{2}, z = 3 + 2 i$

Ta có $\{\begin{cases} I A = 2 \\ I B = 2 \\ A B = 2 \sqrt{3} \end{cases} \Rightarrow A, B$ thuộc đường tròn tâm I, bán kính bằng 2 và $\hat{A I B} = 120^{0}$ .

Gọi H là trung điểm của AB, ta có $I H ⊥ A B \Rightarrow I H = I A . \sin 30^{0} = 1$

$\Rightarrow H$ thuộc đường tròn tâm I, bán kính bằng 1.

Gọi M là điểm biểu diễn cho $z_{1} + z_{2}$ . Ta có $\vec{O M} = 2 \vec{O H} \Rightarrow V_{O}^{2} (H) = M$

Mà H thuộc đường tròn (C) tâm I, bán kính bằng 1 nên là ảnh của $M \in (C^{'})$ qua phép vị tự tâm O, tỉ số 2.

Suy ra $(C^{'})$ có tâm J(6;2) và bán kính $R^{'} = 2$ . $\Rightarrow |z_{1} + z_{2} - 6 - 4 i| = 2$ .

$P = |z_{1} + z_{2} - 3 - 5 i| = |(z_{1} + z_{2} - 6 - 4 i) + (3 - i)|$

$||z_{1} + z_{2} - 6 - 4 i| - |3 - i|| \leq P \leq |z_{1} + z_{2} - 6 - 4 i| + |3 - i| \Leftrightarrow \sqrt{10} - 2 \leq P \leq \sqrt{10} + 2$

$P = \sqrt{10} - 2 \Leftrightarrow \{\begin{cases} z_{1} + z_{2} - 6 - 4 i = k (3 + i) \\ |z_{1} + z_{2} - 6 - 4 i| = 2 \end{cases}$ …..

Vậy $m = \sqrt{10} + 2; n = \sqrt{10} - 2$ . Suy ra $2 n + m = 3 \sqrt{10} - 2$

Câu 50:

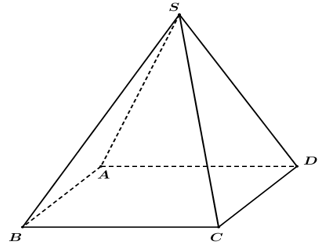
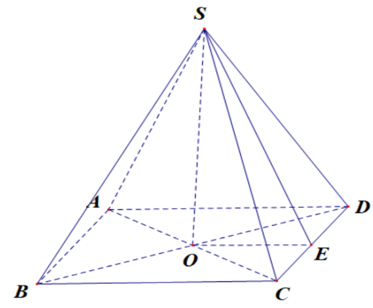
Trong không gian (Oxyz), cho A(1;-3;-2). B(5;1;0). Gọi (S) là mặt cầu đường kính AB. Trong các hình chóp đều có đỉnh A nội tiếp trong mặt cầu (S), gọi A.MNPQ là hình chóp có thể tích lớn nhất. Phương trình mặt cầu tâm B và tiếp xúc với mặt phẳng (MNPQ) là

$A . {(x - 5)}^{2} + {(y - 1)}^{2} + z^{2} = 4$

$B . {(x - 5)}^{2} + {(y - 1)}^{2} + z^{2} = 16$

$C . {(x - 5)}^{2} + {(y - 1)}^{2} + z^{2} = 2$

$D . {(x - 5)}^{2} + {(y - 1)}^{2} + z^{2} = 8$

Xem đáp án

Chọn A

Mặt cầu (S) có tâm I(3;-1;-1), bán kính R=3.

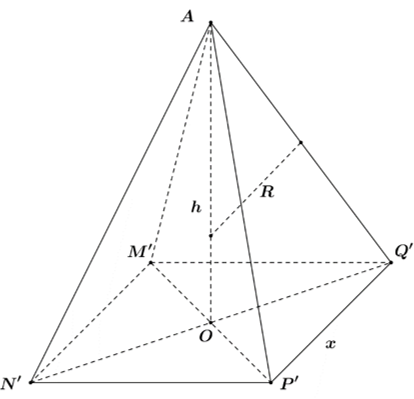
Gọi hình chóp đều nội tiếp trong mặt cầu (S) có cạnh đáy là x và đường cao là h.

Bán kính mặt cầu ngoại tiếp hình chóp đều là $R = \frac{\frac{x^{2}}{2} + h^{2}}{2 h}$

$R = 3 \Leftrightarrow \frac{\frac{x^{2}}{2} + h^{2}}{2 h} = 3 \Leftrightarrow x^{2} + 2 h^{2} = 12 h \Leftrightarrow x^{2} = 12 h - 2 h^{2}$

Thể tích khối chóp đều nội tiếp trong mặt cầu là

$V = \frac{1}{3} x^{2} h = \frac{1}{3} (12 h - 2 h^{2}) h = \frac{1}{3} h . h . (12 - 2 h) \leq \frac{1}{3} {(\frac{h + h + 12 - 2 h}{3})}^{3} = \frac{64}{3}$ .

Dấu bằng xảy ra khi $12 h - 2 h = h \Leftrightarrow h = 4 \Rightarrow x = 4$ .

Vậy thể tích khối chóp đều nội tiếp trong khối cầu có thể tích lớn nhất khi đường cao bằng cạnh đáy và bằng 4. Khi đó gọi I là tâm hình vuông MNPQ, ta có

$\vec{A I} = \frac{A I}{A B} . \vec{A B} \Leftrightarrow \vec{A I} = \frac{2}{3} . \vec{A B} \Rightarrow \{\begin{cases} x - 1 = \frac{8}{3} \\ y + 3 = \frac{8}{3} \\ z + 2 = \frac{4}{3} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{11}{3} \\ y = - \frac{1}{3} \\ z = - \frac{2}{3} \end{cases} \Rightarrow I (\frac{11}{3}; - \frac{1}{3}; - \frac{2}{3})$

Mặt phẳng $(α)$ qua I và có véc tơ pháp tuyến $\vec{A B}$

Phương trình mp $(α)$ là:

Hay $(α) : 2 x + 2 y + z - 6 = 0$

Ta thấy $H, K \in (α), O \notin (α)$ . Vậy có hai điểm thuộc mp $(α)$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi THPT Quốc gia môn Toán học năm 2022 chọn lọc, có lời giải (30 đề)

Đề thi THPT Quốc gia môn Toán học năm 2022 chọn lọc, có lời giải ( Đề 10)

Danh sách câu hỏi

Bài thi liên quan