Trắc nghiệm Tổng ba góc của một tam giác có đáp án (Nhận biết)
-
1945 lượt thi
-
29 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Câu 1: Tổng ba góc trong một tam giác bằng?
 Xem đáp án
Xem đáp án
Tổng ba góc trong một tam giác bằng
Đáp án cần chọn là B
Câu 2:
Câu 2: Cho tam giác MNP, khi đó bằng
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔMNP, ta có:
= =
Đáp án cần chọn là: B
Câu 3:
Câu 3: Cho tam giác DEF. Trên tia đối của tia EF lấy điểm M, phát biểu nào dưới đây là sai:
 Xem đáp án
Xem đáp án
Xét tam giác DEF có là góc ngoài của tam giác DEF
( tính chất góc ngoài của tam giác)
Và (hai góc kề bù).
Đáp án cần chọn B
Câu 4:
Câu 4: Góc ngoài của tam giác là:
 Xem đáp án
Xem đáp án
Góc ngoài của tam giác là góc kề bù với một góc của tam giác và bằng tổng của hai góc trong không kề với nó.
Đáp án A
Câu 5:
Câu 5: Ta có hình vẽ sau:
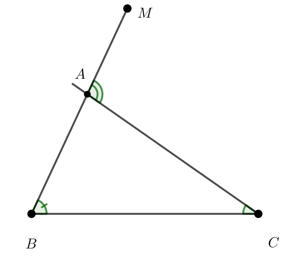
Phát biểu nào dưới đây sai?
 Xem đáp án
Xem đáp án
Xét , ta có: là góc ngoài của tam giác
(tính chất góc ngoài của tam giác). Do đó A đúng
. Do đó B đúng
Và . Do đó C đúng
Đáp án cần chọn là D.
Câu 6:
Câu 6: Cho vuông tại A. Khi đó:
 Xem đáp án
Xem đáp án
Vì tam giác ABC vuông tại A nên
Đáp án cần chọn là: A
Câu 7:
Câu 7: Cho có . Khi đó tam giác ABC là:
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Vậy ΔABC là tam giác vuông.
Đáp án cần chọn là: B
Câu 8:
Câu 8: Cho có . Số đo góc B:
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Đáp án cần chọn là A
Câu 9:
Câu 9: Cho có . Số đo góc A :
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Đáp án cần chọn là A
Câu 10:
Câu 10: Cho hình vẽ sau. Tính số đo x
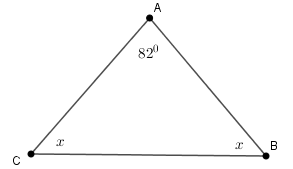
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Hay
Đáp án cần chọn là C
Câu 11:
Câu 11: Cho hình vẽ sau. Tính số đo x
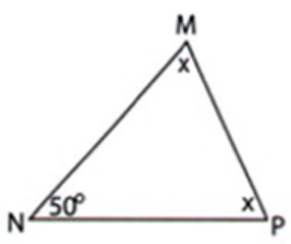
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔMNP , ta có:
Đáp án cần chọn là C
Câu 12:
Câu 12: Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc
 Xem đáp án
Xem đáp án
Giả sử tam giác ABC có ba góc bằng nhau
Lại có:
Vậy
Đáp án cần chọn là D
Câu 13:
Câu 13: Cho tam giác ABC có . Tính số đo góc B
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Mà (gt) nên
Đáp án cần chọn là D
Câu 14:
Câu 14: Cho hình vẽ sau. Tính số đo x
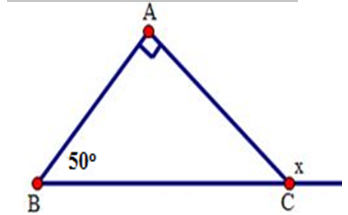
 Xem đáp án
Xem đáp án
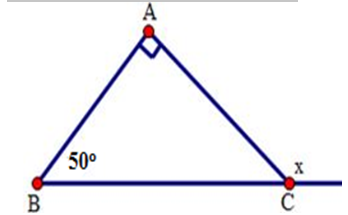
Ta có x là số đo ngoài tại đỉnh C của tam giác ABC nên
Đáp án cần chọn là D
Câu 15:
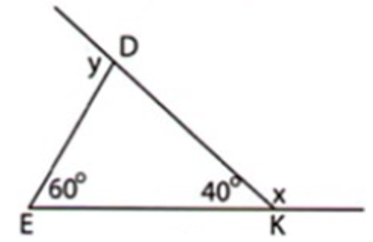
Câu 15: Cho hình sau. Tính x và y
 Xem đáp án
Xem đáp án
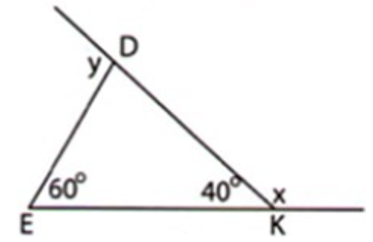
Ta có: là góc ngoài tại đỉnh D nên
Ta có: và là hai góc kề bù nên
Đáp án cần chọn là D
Câu 16:
Câu 16: Cho tam giác ABC biết rằng số đo các góc tỉ lệ với 2; 3; 4. Tính
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Theo đề bài ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Vậy các góc của tam giác ABC là:
Đáp án cần chọn là A
Câu 17:
Câu 17: Cho tam giác ABC biết rằng số đo các góc tỉ lệ với 3; 4; 5. Tính
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC , ta có:
Theo đề bài ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Vậy các góc của tam giác ABC là:
Đáp án cần chọn là A
Câu 18:
Câu 18: Tam giác ABC có . Số đo góc B và góc C lần lượt là:
 Xem đáp án
Xem đáp án
Xét tam giác ABC có:
Theo đề bài ta có:
Từ (1) ta có:
Thế vào (2) ta được:
Đáp án cần chọn là A
Câu 19:
Tam giác ABC có . Số đo góc B và góc C lần lượt là:
 Xem đáp án
Xem đáp án
Xét tam giác ABC có:
Theo đề bài ta có:
Thay (2) vào (1) ta được:
Đáp án cần chọn là B
Câu 20:
Câu 20: Cho tam giác ABC có . Tia phân giác của góc C cắt cạnh AB tại M. Tính
 Xem đáp án
Xem đáp án
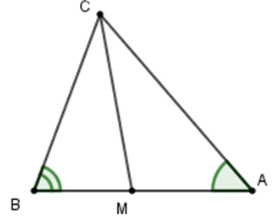
Xét tam giác ABC có (định lí tổng ba góc trong tam giác) mà . Suy ra:
Vì CM là tia phân giác của góc BCA nên
Ta có là góc ngoài tại đỉnh M của tam giác BCM nên ta có:
Lại có: (hai góc kề bù) suy ra
Vậy
Đáp án cần chọn là D
Câu 21:
Câu 21: Cho tam giác ABC có . Tia phân giác của góc A cắt cạnh BC tại D. Tính
 Xem đáp án
Xem đáp án
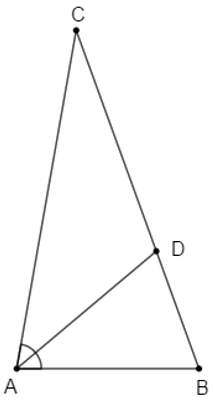
Áp dụng định lí tổng ba góc trong một tam giác vào ta có:
Vì AD là tia phân giác góc nên
Ta có : là góc ngoài đỉnh D của tam giác ABD nên ta có:
Vậy
Đáp án cần chọn là D
Câu 22:
Câu 22: Cho tam giác ABC có . Tính và ?
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc trong một tam giác vào ta có:
Vì AD là tia phân giác góc nên
Ta có : là góc ngoài đỉnh D của tam giác ABD nên ta có:
Vậy
Đáp án cần chọn là D
Câu 23:
Câu 23: Cho tam giác ABC có . Tính và ?
 Xem đáp án
Xem đáp án
Theo định lí về tổng ba góc trong tam giác ta có:
Lại có: (2)
Thay (2) vào (1) ta có:
Suy ra
Đáp án cần chọn là C
Câu 24:
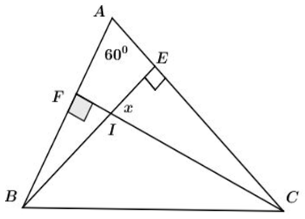
Câu 24: Cho hình vẽ sau. Tính số đo góc x?
 Xem đáp án
Xem đáp án
Xét tam giác ACF có:
Xét ta có:
Đáp án cần chọn là C
Câu 25:
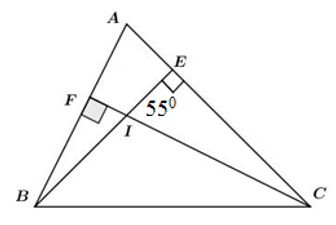
Câu 25: Cho hình vẽ sau. Biết , tính số đo góc A
 Xem đáp án
Xem đáp án
Áp dụng định lí tổng ba góc của một tam giác vào , ta có:
Hay
Áp dụng định lí tổng ba góc của một tam giác vào , ta có:
Vậy
Đáp án cần chọn là B
Câu 26:
Câu 26: Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC tại E. Chọn câu sai:
 Xem đáp án
Xem đáp án
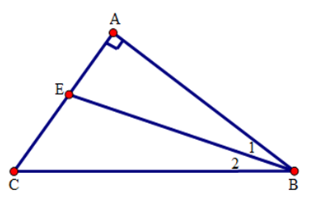
Góc BEC là góc ngoài của đỉnh E của ta giác AEC nên
Vậy góc BEC là góc tù nên và
Vậy A,C,D đúng, B sai
Đáp án cần chọn là B
Câu 27:
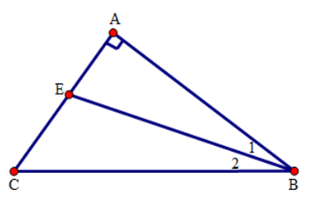
Câu 27: Cho hình vẽ có . Tính và
 Xem đáp án
Xem đáp án
Theo giả thiết
Mặt khác do tam giác ABC vuông tại A nên
Từ đó ta có
Do BE là tia phân giác của góc ABC nên
Sử dụng tính chất góc ngoài của tam giác ta tìm được:
Và
Vậy
Đáp án cần chọn là C
Câu 28:
Câu 28: Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo biết
 Xem đáp án
Xem đáp án
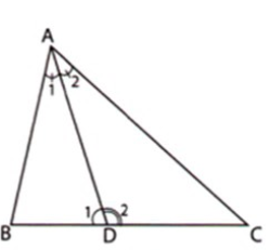
Ta có: là góc ngoài tại đỉnh D của tam giác ABD nên
Ta có: là góc ngoài tại đỉnh D của tam giác ADC nên
Từ (1) và (2) ta có:
Vì AD là tia phân giác nên và (gt) suy ra
Mặt khác và là hai góc kề bù nên
Từ (3) và (4) suy ra :
Vậy
Đáp án cần chọn là C
Câu 29:
Câu 29: Cho tam giác ABC có : và . Tia phân giác của góc C cắt AB tại D. Tính và
 Xem đáp án
Xem đáp án
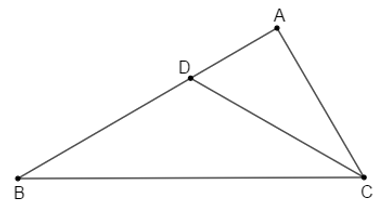
Áp dụng định lí tổng ba góc của một tam giác vào , ta có:
(vì )
Mặt khác (gt) nên
Vì CD là phân giác của nên
là góc ngoài tại đỉnh D của nên ta có:
và là hai góc kề bù nên
Đáp án cần chọn là D
