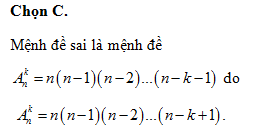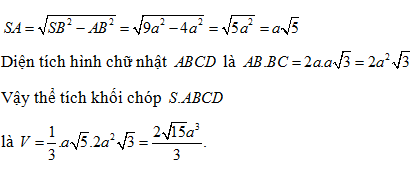50 câu hỏi trắc nghiệm thuộc Bộ đề thi Toán THPT Quốc gia năm 2022 có lời giải (Đề số 19)

Câu 1:

Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?

A. $y = 2 x^{4} - x^{2} + 1$

B. $y = - x^{4} + x^{2} + 1$

C. $y = - x^{4} + 2 x^{2} + 1$

D. $y = x^{4} - 2 x^{2} + 1$

Xem đáp án

Câu 2:

Số nghiệm $\frac{\sin 2 x}{\cos x + 1} = 0$ của phương trình trên đoạn $[0; 2020 π]$ là

A. 3030

B. 2020

C. 3031

D. 4040

Xem đáp án

Câu 3:

Số nghiệm của phương trình $\log_{4} (3 x^{2} + x) = \frac{1}{2}$ là

A. 1

B. 5

C. 0

D. 2

Xem đáp án

Câu 4:

Với a là số thực dương khác 1 tùy ý, $\log_{a^{5}} a^{4}$ bằng

A. $\frac{1}{5}$

B. $\frac{4}{5}$

C. 20

D. $\frac{5}{4}$

Xem đáp án

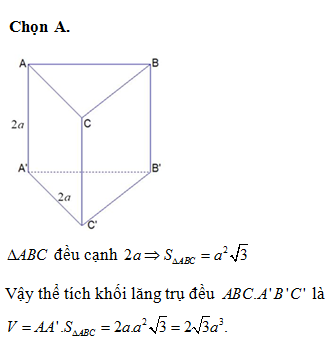
Chọn B.

Ta có $\log_{a^{5}} a^{4} = \frac{4}{5} \log_{a} a = \frac{4}{5} .$

Câu 5:

Khối chóp có một nửa diện tích đáy là S, chiều cao là 2h thì có thể tích là:

A. $V = \frac{1}{2} S . h$

B. $V = \frac{1}{3} S . h$

C. $V = S . h$

D. $V = \frac{4}{3} S . h$

Xem đáp án

Chọn D.

Áp dụng công thức thể tích khối chóp ta có: $V = \frac{1}{3} .2 S .2 h = \frac{4}{3} S . h$

Câu 6:

Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích toàn phần của hình trụ (T) là:

A. $S_{t p} = π R h + 2 π R^{2}$

B. $S_{t p} = π R h + π R^{2}$

C. $S_{t p} = 2 π R l + 2 π R^{2}$

D. $S_{t p} = π R l + π R^{2}$

Xem đáp án

Chọn C.

Ta có: $S_{t p} = 2 π R l + 2 π R^{2} = 2 π R h + 2 π R^{2}$ nên chọn đáp án C.

Câu 7:

Nghiệm của phương trình 2cosx +1 = 0 là

A. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ .$

B. $[\begin{array}{l} x = \frac{π}{3} + k 2 π \\ x = \frac{2 π}{3} + k 2 π \end{array}, k \in ℤ .$

C. $x = \pm \frac{2 π}{3} + k π, k \in ℤ .$

D. $x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ .$

Xem đáp án

Chọn D.

Ta có $2 \cos x + 1 = 0 \Leftrightarrow \cos x = - \frac{1}{2} = \cos (\frac{2 π}{3}) \Leftrightarrow x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ .$

Câu 8:

Gọi S là tập các giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{x - 3}{x^{2} - 2 m x + 2 m^{2} - 9}$ có đúng đường tiệm cận. Số phần tử của S là

A. 6

B. 7

C. 4

D. 5

Xem đáp án

Câu 9:

Nhà bạn Minh cần khoan một cái giếng nước. Biết rằng giá tiền của mét khoan đầu tiên là 200.000đ và kể từ mét khoan thứ hai, giá tiền của mỗi mét sau tăng thêm 7% so với giá tiền của mét khoan ngay trước nó. Hỏi nếu nhà bạn An khoan cái giếng sâu 30m thì hết bao nhiêu tiền (làm tròn đến hàng nghìn)?

A. $18895000 đ$

B. $142285 đ$

C. $18892000 đ$

D. $1889220 đ$

Xem đáp án

Câu 10:

Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn $(C) : x^{2} + y^{2} - 2 x - 4 y - 11 = 0$ . Tìm bán kính của đường tròn (C’) là ảnh của đường tròn (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2020 và phép tịnh tiến theo véctơ $\vec{v} = (2019; 2020)$ là:

A. 16

B. 8080

C. 32320

D. 4

Xem đáp án

Câu 11:

Tính đạo hàm của hàm số $f (x) = \sin^{2} x - \cos 2 x$

A. $f^{'} (x) = 3 \sin 2 x$

B. $f^{'} (x) = 2 \sin x + \sin 2 x$

C. $f^{'} (x) = - \sin 2 x$

D. $f^{'} (x) = 2 \sin x + 2 \sin 2 x$

Xem đáp án

Chọn A.

Ta có $f (x) = \sin^{2} x - \cos 2 x .$

$\Rightarrow f' (x) = 2 \sin x . \cos x + \sin 2 x .2 = \sin 2 x + 2 \sin 2 x = 3 \sin 2 x .$

Câu 12:

Biết giới hạn $\lim \frac{3 - 2 n}{5 n + 1} = \frac{a}{b}$ trong đó $a, b \in Z$ và $\frac{a}{b}$ tối giản. Tính ab.

A. 6

B. 3

C. - 10

D.15

Xem đáp án

Chọn C.

Ta có $\lim \frac{3 - 2 n}{5 n + 1} = \lim \frac{\frac{3}{n} - 2}{5 + \frac{1}{n}} = - \frac{2}{5} .$

Vậy $a b = - 10.$

Câu 13:

Cho a là số thực dương thỏa mãn $a \neq 10$ , mệnh đề nào dưới đây sai?

A. $\log (\frac{100}{a}) = 2 - \log a$

B. $\log (a^{10}) = a$

C. $\log (10^{a}) = a$

D. $\log (1000. a) = 3 + \log a$

Xem đáp án

Chọn B.

Ta có $\log a^{10} = 10 \log a \neq a .$

Câu 14:

Cho mặt cầu (S) có tâmO, bán kính .Biết khoảng cách từ tâm O đến mặt phẳng bằng $(α)$ . Mặt phẳng $(α)$ cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính bằng

A. $r = 10$

B. $r = 2 \sqrt{5}$

C. $r = \sqrt{52}$

D. r = 2

Xem đáp án

Câu 15:

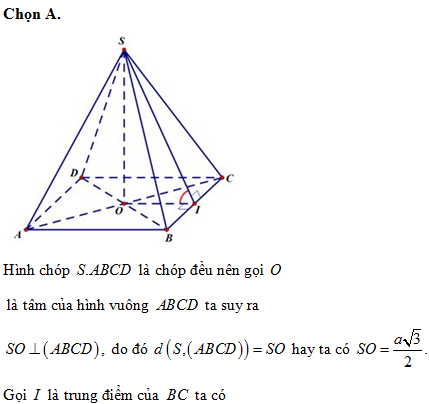
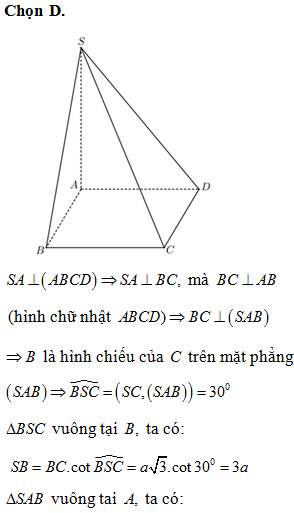
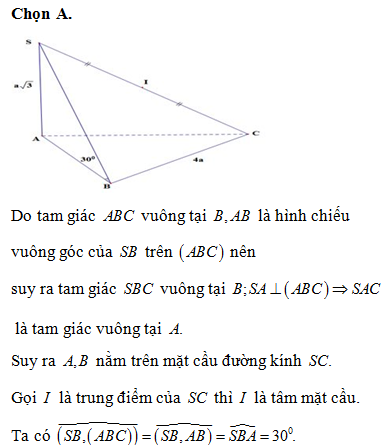
Cho hình chóp đều S. ABCD cạnh đáy bằng a, $d (S, (A B C D)) = \frac{a \sqrt{3}}{2}$ Góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) bằng

A. $60^{0}$

B. $90^{0}$

C. $45^{0}$

D. $30^{0}$

Xem đáp án

Câu 16:

Tiệm cận ngang của đồ thị hàm số $y = \frac{x - 1}{1 - 2 x}$ là:

A. $y = - 1$

B. $x = \frac{1}{2}$

C. $y = \frac{1}{2}$

D. $y = - \frac{1}{2}$

Xem đáp án

Câu 17:

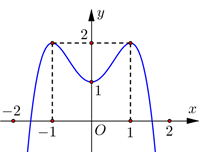
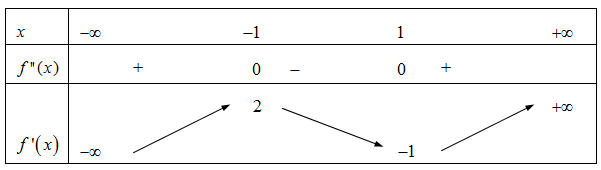
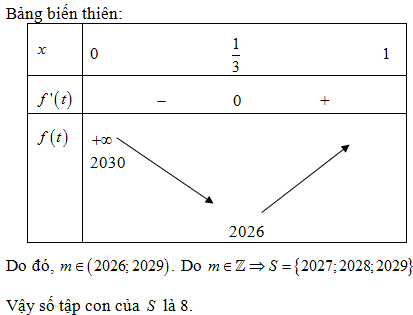
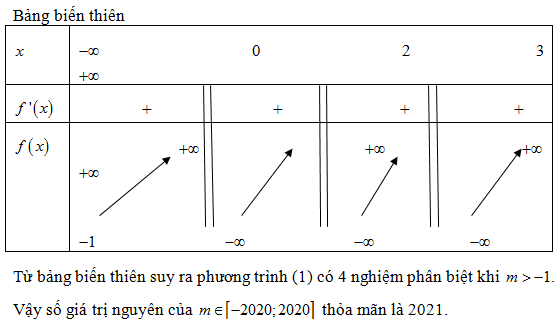
Cho hàm số y =f(x) có bảng biến thiên như sau:

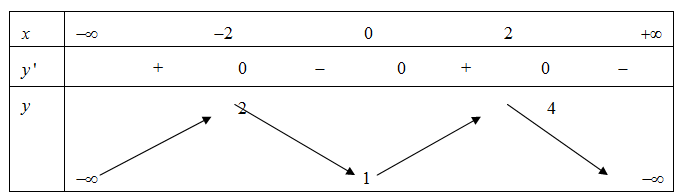
Giá trị cực tiểu của hàm số đã cho bằng

A. 1

B. 4

C. 2

D. 0

Xem đáp án

Chọn A.

Dựa vào bảng biến thiên ta thấy giá trị cực tiểu của hàm số đã cho bằng 1.

Câu 18:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi , SA = a, $A C = 2 a; B D = 3 a$ vuông góc với mặt đáy. Thể tích của khối chóp S.ABCD là

A. $2 a^{3}$

B. $a^{3}$

B. $\frac{2}{3} a^{3}$

D. $4 a^{3}$

Xem đáp án

Câu 19:

Tập nghiệm của bất phương trình ${(\frac{1}{3})}^{x + 2} \geq 9$

A. $(- \infty; - 4]$

B. $[- 4; + \infty)$

C. $(- \infty; 4]$

D. $[0; + \infty)$

Xem đáp án

Câu 20:

Cho hàm số $y = \frac{x + a}{b x - 2}$ $(a b \neq - 2)$ . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(-1;2) song song với đường thẳng $d : 3 x - y - 7 = 0$ . Khi đó giá trị của a-3b bằng

A. $- 13$

B. 4

C. 32

D. 7

Xem đáp án

Câu 21:

Cho tập hợp A gồm có 2021 phần tử. Số tập con của A có số phần tử $\geq 1011$ bằng

A. $2^{2020}$

B. $2^{2021}$

C. $2020$

D. $2^{2019}$

Xem đáp án

Câu 22:

Chọn mệnh đề sai trong các mệnh đề sau:

A. $C_{n}^{k} = C_{n}^{n - k}$

B. $C_{n}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k}$

C. $A_{n}^{k} = n (n - 1) (n - 2) ... (n - k - 1)$

D. $C_{n}^{k} = \frac{A_{n}^{k}}{k!}$

Xem đáp án

Câu 23:

Cho hàm số $y = x (1 - x) (x^{2} - 3 x + 2)$ có đồ thị (C). Mệnh đề nào dưới đây đúng?

A. (C) cắt trục hoành tại điểm.

B. (C) cắt trục hoành tại điểm phân biệt.

C. (C) cắt trục hoành tại điểm phân biệt.

D. (C) cắt trục hoành tại điểm phân biệt.

Xem đáp án

Câu 24:

Cho hình lăng trụ ABC.A’B’C’. Gọi I, J, Klần lượt là trọng tâm của các tam giác ABC, AA’C,A’B’C’. Mặt phẳng nào sau đây song song với mặt phẳng (IJK)?

A. $(A^{'} B C^{'})$

B. $(A A' B)$

C. $(B B' C)$

D. $(A A^{'} C)$

Xem đáp án

Câu 25:

Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật , $A B = a; A D = 4 a; S A = a \sqrt{15}$ , $S A ⊥ (A B C D)$ M là trung điểm của AD , N thuộc cạnh BC sao cho BC = 4BN . Khoảng cách gữa MN và SD là

A. $\frac{2 \sqrt{33} a}{11}$

B. $\frac{2 \sqrt{690} a}{23}$

C. $\frac{a \sqrt{33}}{11}$

D. $\frac{\sqrt{690} a}{23}$

Xem đáp án

Câu 26:

Tính thể tích khối lăng trụ tam giác đều ABC.A’B’C’ biết tất cả các cạnh của lăng trụ đều bằng 2a.

A. $2 \sqrt{3} a^{3}$

B. $\frac{\sqrt{3} a^{3}}{2}$

C. $\frac{\sqrt{3} a^{3}}{6}$

D. $\frac{2 \sqrt{3} a^{3}}{3}$

Xem đáp án

Câu 27:

Cho 40 thẻ được đánh số từ 1 đến 40, chọn ngẫu nhiên 3 thẻ. Xác suất để tổng các số ghi trên 3 thẻ được chọn là một số chia hết cho 3 bằng

A. $\frac{9}{95}$

B. $\frac{127}{380}$

C. $\frac{11}{380}$

D. $\frac{11}{190}$

Xem đáp án

Câu 28:

Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên. Tìm số nghiệm của phương trình 2f(x)-3=0.

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Câu 29:

Gọi S là tập giá trị nguyên $m \in [- 2020; 2020]$ để phương trình $2 \sin^{2} x + m \sin 2 x = 2 m$ vô nghiệm.Tính tổng các phần tử của S

A. $S = 2020$

B. $S = 0$

C. $S = - 1$

D. $S = 1$

Xem đáp án

Câu 30:

Cho hàm số f(x) liên tục trên R và hàm số f’(x) có bảng biến thiên như sau. Tìm mệnh đề đúng?

A. Hàm số y = f(x) có 2 điểm cực tiểu và 1 điểm cực đại .

B. Hàm số y = f(x) có 1 điểm cực tiểuvà 1 điểm cực đại

C. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.

D. Hàm số y = f(x) có 1 điểm cực tiểu và 2 điểm cực đại .

Xem đáp án

Câu 31:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật vớIab = 2a, $B C = a \sqrt{3}$ . Cạnh bên SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc . Tính thể tích của khối chóp S.ABCD theo a.

A. $V = \frac{\sqrt{15} a^{3}}{3}$

B. $V = \frac{\sqrt{3} a^{3}}{3}$

C. $V = 2 \sqrt{3} a^{3}$

D. $V = \frac{2 \sqrt{15} a^{3}}{3}$

Xem đáp án

Câu 32:

Cho hàm số f(x) có đạo hàm $f^{'} (x) = {(x - 2)}^{2019} {(x^{2} - x - 2)}^{2020} {(x + 3)}^{3}$ . Số điểm cực trị của hàm số f(|x|) là

A. 5

B. 1

C. 2

D. 3

Xem đáp án

Câu 33:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của tham số m để phương trình $|f (\cos x)| = - 2 m + 3$ có $[0; 2 π]$ nghiệm thuộc khoảng là

A. $\{1\}$

B. $[1; \frac{3}{2}]$

C. $[1; \frac{3}{2})$

D. $(0; 1)$

Xem đáp án

Câu 34:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng 3a. Gọi M thuộc cạnh B’C’ sao cho $M C' = 2 M B'$ , N thuộc cạnh AC sao cho AC = 4NC Mặt phẳng (A’MN) cắt cạnh BC tại Q. Tính thể tích V khối đa diện $C N Q . C' A' M$ .

A. $V = \frac{189 \sqrt{3} a^{3}}{64}$

B. $V = \frac{63 \sqrt{3} a^{3}}{32} .$

C. $V = \frac{26 \sqrt{3} a^{3}}{16} .$

D. $V = \frac{31 \sqrt{3} a^{3}}{16} .$

Xem đáp án

Câu 35:

Cho lăng trụ tam giác đều ABC.A’B’C’ có AA’=a. Khoảng cách giữa AB’ và CC’ bằng $a \sqrt{3}$ . Thể tích khối lăng trụ ABC.A’B’C’

A. $\frac{2 a^{3} \sqrt{3}}{3} .$

B. $a^{3} \sqrt{3} .$

C. $\frac{a^{3} \sqrt{3}}{2}$

D. $\frac{a^{3} \sqrt{3}}{3}$

Xem đáp án

Câu 36:

Giá trị m để hàm số $y = \frac{2^{- x} - 2}{2^{- x} - m}$ nghịch biến trên (-1;0) là

A. $m > 2$

B. $m < 2$

C. $m \leq 0$

D. $m \leq 1$

Xem đáp án

Câu 37:

Gọi S là tập các giá trị m nguyên m để phương trình $9. {(\sqrt{10} + 3)}^{x} + {(\sqrt{10} - 3)}^{x} - m + 2020 = 0$ có đúng hai nghiệm âm phân biệt. Số tập con của S là

A. 7

B.3

C. 6

D. 8

Xem đáp án

Câu 38:

Giá trị lớn nhất của hàm số $f (x) = x^{3} - 15 x$ trên đoạn [-4;1] bằng

A. 22

B. $- 14$

C. $- 10 \sqrt{5}$

D. $10 \sqrt{5}$

Xem đáp án

Câu 39:

Cho mặt cầu có diện tích bằng $\frac{8 π a^{2}}{3}$ , khi đó bán kính mặt cầu là

A. $R = \frac{a \sqrt{6}}{2}$

B. $R = \frac{a \sqrt{3}}{3}$

C. $R = \frac{a \sqrt{2}}{3}$

D. $R = \frac{a \sqrt{6}}{3}$

Xem đáp án

Câu 40:

Một khối nón có đường sinh bằng 2a và diện tích xung quanh của mặt nón bằng $π a^{2}$ . Tính thể tích của khối nón đã cho?

A. $V = \frac{π a^{3} \sqrt{15}}{12}$

B. $V = \frac{π a^{3} \sqrt{15}}{24}$

C. $V = \frac{π a^{3} \sqrt{7}}{24}$

D. $V = \frac{π a^{3} \sqrt{15}}{8}$

Xem đáp án

Câu 41:

Cho hàm số y =f(x) có bảng biến thiên như sau:

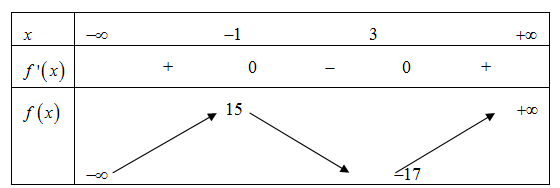
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(- 17; 15)$

B. $(- \infty; - 3)$

C. $(3; + \infty)$

D. $(- 1; 3)$

Xem đáp án

Chọn D.

Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng (-1;3)

Câu 42:

Cho tứ diện SABC có đáy ABC là tam giác vuông tại B với $B C = 4 a, S A = a \sqrt{3}$ , $S A ⊥ (A B C)$ và cạnh bên SB tạo với mặt đáy góc $30 °$ Tính thể tích khối cầu ngoại tiếp SABC.

A. $V = \frac{28 \sqrt{7} π a^{3}}{3}$

B. $V = 28 \sqrt{7} π a^{3}$

C. $V = 28 π a^{3}$

D. $V = \frac{20 \sqrt{5} π a^{3}}{6}$

Xem đáp án

Câu 43:

Biết đồ thị hàm số $y = x^{3} + 3 x^{2} - 1$ có hai điểm cực trị A,B. Khi đó phương trình đường trung trực của đoạn AB là

A. $x - 2 y - 2 = 0$

B. $2 x + y - 1 = 0$

C. $2 x + y + 1 = 0.$

D. $x - 2 y + 3 = 0.$

Xem đáp án

Câu 44:

Cho 2 hàm số $y = \log_{2} (x + 2) (C_{1})$ và $y = \log_{2} x + 1 (C_{2})$ . Goị A,B lần lượt là giao điểm của $(C_{1}); (C_{2})$ với trục hoành, C là giao điểm của $(C_{1})$ và $(C_{2})$ . Diện tích tam giác ABC bằng

A. 3 (đvdt)

B. $\frac{3}{4}$ (đvdt)

C. $\frac{3}{2}$ (đvdt)

D. $\frac{1}{2}$ (đvdt)

Xem đáp án

Câu 45:

Cho hai hàm số $y = x (x - 2) (x - 3) (m - | x |); y = x^{4} - 6 x^{3} + 5 x^{2} + 11 x - 6$ có đồ thị lần lượt là $(C_{1}), (C_{2})$ . Có bao nhiêu giá trị nguyên m thuộc đoạn [-2020;2020] để $(C_{1})$ cắt $(C_{2})$ tại 4 điểm phân biệt?

A. 2021

B. 2019

C. 4041

D. 2020

Xem đáp án

Câu 46:

Số nghiệm của phương trình $e^{\frac{x^{2}}{2} + x - 2020} = \ln (x^{2} - 2) + \frac{x^{2}}{2} - x + 2018$ là

A. 4

B. 2

C. 0

D. 3

Xem đáp án

Câu 47:

Tập xác định của hàm số $y = {(9 - x^{2})}^{\frac{1}{2020}}$ là:

A. $[- 3; 3]$

B. $(- 3; 3)$

C. $(- \infty; - 3) \cup (3; + \infty)$

D. $(- \infty; - 3)$

Xem đáp án

Câu 48:

Cho cấp số nhân $(u_{n})$ biết $u_{4} = 7; u_{10} = 56$ . Tìm công bội q

A. $q = \pm 2$

B. $q = \pm \sqrt{2}$

C. $q = \sqrt{2}$

D. q = 2

Xem đáp án

Câu 49:

Cho một hình nón đỉnh S có độ dài đường sinh bằng 10cm , bán kính đáy bằng 6cm. Cắt hình nón đã cho bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón (N) đỉnh S có chiều cao bằng $\frac{16}{5}$ . Tính diện tích xung quay của khối nón (N) .

A. $S = \frac{48}{10} π {cm}^{2}$

B. $S = \frac{48}{5} π {cm}^{2}$

C. $S = \frac{48}{5} {cm}^{2}$

D. $S = \frac{96}{5} π {cm}^{2}$

Xem đáp án