50 câu hỏi trắc nghiệm thuộc Bộ đề thi Toán THPT Quốc gia năm 2022 có lời giải (Đề số 20)

Câu 1:

Cho giới hạn $\lim_{x \to - 4} \frac{x^{2} + 3 x - 4}{x^{2} + 4 x} = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Tính giá trị biểu thức $a^{2} - b^{2} .$

A. $- 9$

B. 41

C. 9

D. 14

Xem đáp án

Câu 2:

Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng (ABC) biết $A B = A C = a, B C = a \sqrt{3} .$ Tính góc giữa hai mặt phẳng (SAB) và (SAC)

A. $45^{0} .$

B. $30 °$

C. $60 °$

D. $90 °$

Xem đáp án

Câu 3:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào

A. $y = (x - 1) {(x - 2)}^{2} .$

B. $y = (x - 1) {(x + 2)}^{2} .$

C. $y = {(x - 1)}^{2} (x + 2) .$

D. $y = {(x + 1)}^{2} (x + 2) .$

Xem đáp án

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a, S D = \frac{3 a}{2},$ hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB Tính theo a thể tích khối chóp S.ABCD

A. $\frac{a^{3}}{4} .$

B. $\frac{2 a^{3}}{3} .$

C. $\frac{a^{3}}{3} .$

D. $\frac{a^{3}}{2} .$

Xem đáp án

Câu 5:

Gọi $M (x_{0}; y_{0})$ là điểm thuộc đồ thị hàm số $y = \log_{3} x .$ Tìm điều kiện của $x_{0}$ để điểm M nằm phía trên đường thẳng y = 2

A. $x_{0} > 9.$

B. $x_{0} > 0.$

C. $x_{0} < 2.$

D. $x_{0} > 2.$

Xem đáp án

Câu 6:

Cho hình chóp S.ABCD đáy là hình vuông tâm cạnh a,SO vuông góc với mặt phẳng (ABCD) và SO = a Khoảng cách giữa SC và AB bằng:

A. $\frac{a \sqrt{3}}{15} .$

B. $\frac{2 a \sqrt{3}}{15} .$

C. $\frac{2 a \sqrt{5}}{5} .$

D. $\frac{a \sqrt{5}}{5} .$

Xem đáp án

Câu 7:

Cho dãy số $(u_{n})$ là cấp số nhân có số hạng đầu $u_{1} = 1,$ công bội q=2 Tổng ba số hạng đầu của cấp số nhân là

A. 3

B. 7

C. 9

D. 5

Xem đáp án

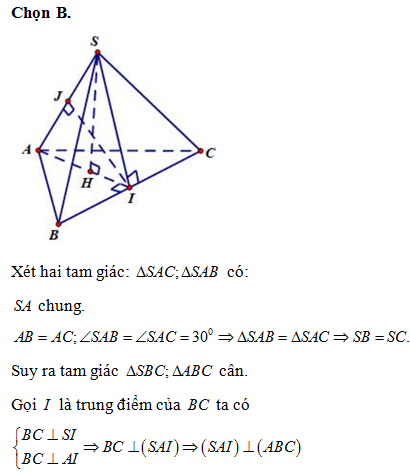
Chọn B.

Ta có $S_{3} = u_{1} \frac{q^{3} - 1}{q - 1} = 1. \frac{2^{3} - 1}{2 - 1} = 7.$

Câu 8:

Cho mặt cầu S(O;r), mặt phẳng (P) cách tâm O một khoảng bằng $\frac{r}{2}$ cắt mặt cầu (S) theo giao tuyến là một đường tròn. Hãy tính theo r chu vi của đường tròn là giao tuyến của mặt phẳng (P) và mặt cầu (S)

A. $π r \sqrt{3} .$

B. $πr$

C. $\frac{π r \sqrt{3}}{4}$

D. $\frac{π r \sqrt{3}}{2}$

Xem đáp án

Câu 9:

Đạo hàm của hàm số $y = \frac{\ln (x^{2} + 1)}{x}$ tại điểm $x = 1$ là $y' (1) = a \ln 2 + b, (a, b \in ℤ) .$ Tính a - b

A. 2

B. -1

C. 1

D. -2

Xem đáp án

Câu 10:

Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58% / tháng (không kỳ hạn). Hỏi bạn An phải gửi ít nhất bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng?

A. 46

B. 45

C. 42

D.40

Xem đáp án

Câu 11:

Thể tích của khối nón có chiều dài đường sinh bằng 3 và bán kính đáy bằng 2 là

A. $\frac{2 π \sqrt{5}}{3} .$

B. $\frac{4 π \sqrt{5}}{3} .$

C. $\frac{π \sqrt{5}}{3} .$

D. $\frac{4 π}{3} .$

Xem đáp án

Câu 12:

Trên giá sách có 6 quyển sách toán khác nhau, 7 quyển sách văn khác nhau và 8 quyển sách Tiếng anh khác. Hỏi có bao nhiêu cách lấy 2 quyển thuộc 2 môn khác nhau?

A. 146

B. 336

C. 420

D. 210

Xem đáp án

Chọn A.

Số cách lấy 2 quyển thuộc 2 môn khác nhau là: $C_{6}^{1} . C_{7}^{1} + C_{6}^{1} . C_{8}^{1} + C_{7}^{1} . C_{8}^{1} = 146.$

Câu 13:

Cho x,y là hai số thực không âm thỏa mãn x+y=1 Giá trị lớn nhất của x,y là:

A. $\frac{1}{4} .$

B. $\frac{1}{2} .$

C. 1

D. 0

Xem đáp án

Câu 14:

Tính tổng tất cả các nghiệm của phương trình $5^{\sin^{2} x} + 5^{\cos^{2} x} = 2 \sqrt{5}$ trên đoạn $[0; 2 π] .$

A. $T = \frac{3 π}{4} .$

B. $T = π .$

C. $T = 4 π .$

D. $T = 2 π .$

Xem đáp án

Câu 15:

Một hộp có 8 quả cầu đỏ khác nhau, 9 quả cầu trắng khác nhau, 10 quả cầu đen khác nhau. Số cách lấy ngẫu nhiên 1 quả cầu trong hộp là?

A. 816

B. 720

C. 4896

D. 27

Xem đáp án

Câu 16:

Cho dãy số $(u_{n})$ với $u_{n} = n^{2} + n + 1$ với $n \in ℕ *$ . Số 21 là số hạng thứ bao nhiêu của dãy số đã cho?

A. 3

B. 5

C. 6

D. 4

Xem đáp án

Câu 17:

Nếu dãy số $(U_{n})$ là cấp số cộng có công sai d thì ta có công thức là

A. $U_{n + 1} = U_{n} - n d, \forall n \in ℕ *$

B. $U_{n + 1} = U_{n} + d^{n}, \forall n \in ℕ *$

C. $U_{n + 1} = U_{n} + n d, \forall n \in ℕ *$

D. $U_{n + 1} = U_{n} + d, \forall n \in ℕ *$

Xem đáp án

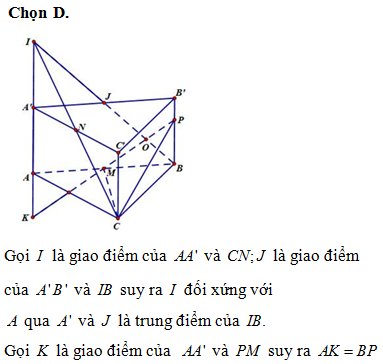
Chọn D.

Theo định nghĩa cấp số cộng ta có: $U_{n + 1} = U_{n} + d, \forall n \in ℕ * .$

Câu 18:

Giới hạn $\lim (2 n^{2} - 1)$ bằng

A. 2

B. $- \infty$

C. $0$

D. $+ \infty$

Xem đáp án

Câu 19:

Cho số tự nhiên n thỏa mãn $C_{n}^{0} + C_{n}^{1} + C_{n}^{2} = 11.$ Số hạng chứa $x^{7}$ trong khai triển ${(x^{3} - \frac{1}{x^{2}})}^{n}$ bằng

A. $- 4.$

B. $- 12 x^{7} .$

C. $9 x^{7} .$

D. $- 4 x^{7} .$

Xem đáp án

Câu 20:

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = \frac{2 x - 4}{x - m}$ có tiệm cận đứng

A. $m < 2$

B. m = 2

C. $m \neq 2$

D. m >2

Xem đáp án

Câu 21:

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số $y = \frac{1}{3} x^{3} - 3 x^{2} + 5 x - 1$

A. có hệ số góc bằng-1

B. song song với trục hoành.

C. song song với đường thẳng x=1

D. có hệ số góc dương

Xem đáp án

Câu 22:

Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y = \frac{1}{\sqrt{\log_{3} (x^{2} - 2 x + 3 m)}}$ có tập xác định là R

A. $[\frac{2}{3}; 10] .$

B. $[\frac{2}{3}; + \infty) .$

C. $(- \infty; \frac{2}{3}) .$

D. $(\frac{2}{3}; + \infty) .$

Xem đáp án

Câu 23:

Thể tích khối cầu có bán kính r là:

A. $\frac{4}{3} π r^{3} .$

B. $4 π r^{3} .$

C. $\frac{1}{3} π r^{3} .$

D. $\frac{4}{3} π r^{2} .$

Xem đáp án

Chọn A.

Công thức tính thể tích khối cầu bán kính r là $V = \frac{4}{3} π r^{3} .$ Chọn đáp án A.

Câu 24:

Hàm số $y = \frac{2 x - 5}{x + 2}$ đồng biến trên:

A. $ℝ \ \{- 2\} .$

B. $(2; + \infty)$

C. R

D. $(- \infty; 2) .$

Xem đáp án

Câu 25:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại $B; A B = 2 a, B C = a, A A' = 2 a \sqrt{3} .$ Thể tích khối lăng trụ ABC.A’B’C’ là

A. $\frac{4 a^{3} \sqrt{3}}{3} .$

B. $2 a^{3} \sqrt{3} .$

C. $4 a^{3} \sqrt{3} .$

D. $\frac{2 a^{3} \sqrt{3}}{3} .$

Xem đáp án

Câu 26:

Tìm tập nghiệm S của phương trình ${(\frac{2020}{2021})}^{4 x} = {(\frac{2021}{2020})}^{2 x - 6}$ là

A. $S = \{- 3\} .$

B. $S = \{1\} .$

C. $S = \{3\} .$

D. $S = \{- 1\} .$

Xem đáp án

Câu 27:

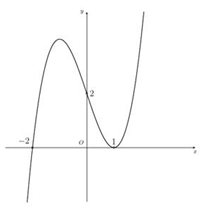
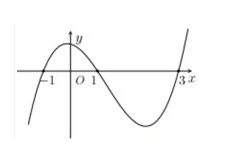
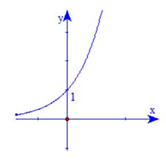
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?

A. $y = 3^{x} .$

B. $y = \log_{\frac{1}{3}} x .$

C. $y = {(\frac{1}{3})}^{x} .$

D. $y = \log_{3} x .$

Xem đáp án

Chọn A.

- Đồ thị hàm số đi qua điểm (0;1) loại B, D.

- Đây là đồ thị của hàm số đồng biến nên loại C.

Câu 28:

Số nghiệm của phương trình $\log_{2020} x + \log_{2021} x = 0$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Câu 29:

Cho hàm số y = f(x) có đạo hàm trên R Mệnh đề nào dưới đây là đúng?

A. Nếu hàm số đạt cực trị tại $x_{0}$ thì đạo hàm đổi dấu khi x qua $x_{0}$

B. Nếu thì hàm số $f' (x_{0}) = 0$ đạt cực trị tại $x_{0}$

C. Nếu $f' (x_{0}) = f " (x_{0}) = 0$ thì hàm số không đạt cực trị tại $x_{0}$

D. Nếu đạo hàm đổi dấu khi $x$ qua $x_{0}$ thì hàm số đạt cực tiểu tại $x_{0}$

Xem đáp án

Chọn A.

Câu 30:

Có bao nhiêu cách sắp xếp 8 học sinh thành một hàng dọc?

A. $8^{8} .$

B. 8

C. 8!

D. 7!

Xem đáp án

Chọn C.

Số cách sắp xếp 8 học sinh thành một àng dọc là: 8!.

Câu 31:

Cho bất phương trình $\log_{\frac{1}{3}} (x^{2} - 2 x + 6) \leq - 2.$ Mệnh đề nào sau đây đúng?

A. Tập nghiệm của bất phương trình là hợp của hai đoạn.

B. Tập nghiệm của bất phương trình là một đoạn.

C. Tập nghiệm của bất phương trình là nửa khoảng.

D. Tập nghiệm của bất phương trình là hợp của hai nửa khoảng.

Xem đáp án

Câu 32:

Cho hàm số y= f(x) có bảng biến thiên như sau:

Hàm số nghịch biến trong khoảng nào?

A. $(4; + \infty)$

B. $(0; 1)$

C. $(- \infty; 2)$

D. $(- 1; 1) .$

Xem đáp án

Câu 33:

Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a góc giữa cạnh bên và mặt đáy bằng $60^{0} .$ Tính thể tích của khối nón có đỉnh là S và đáy là đường tròn ngoại tiếp $Δ A B C .$

A. $\frac{π a^{3} \sqrt{3}}{3} .$

B. $\frac{π a^{3} \sqrt{3}}{6} .$

C. $\frac{2 π a^{3} \sqrt{3}}{3} .$

D. $\frac{4 π a^{3}}{9} .$

Xem đáp án

Câu 34:

Cho hình trụ có bán kính đáy bằng a và chiều cao gấp 2 lần đường kính đáy của hình trụ. Tính diện tích xung quanh của hình trụ.

A. $8 π a .$

B. $4 π a^{2} .$

C. $4 a^{2} .$

D. $8 π a^{2}$

Xem đáp án

Câu 35:

Giới hạn $\lim_{x \to + \infty} \frac{2 x - 1}{2 - 3 x}$ bằng

A. $\frac{2}{3} .$

B. $- 1$

C. $- \frac{2}{3} .$

D. 1

Xem đáp án

Chọn C.

$\lim_{x \to - \infty} \frac{2 x - 1}{2 - 3 x} = \lim_{x \to - \infty} \frac{2 - \frac{1}{x}}{\frac{2}{x} - 3} = - \frac{2}{3} .$

Câu 36:

Có bao nhiêu cách chọn một bạn lớp trưởng và một bạn lớp phó từ một lớp học gồm 35 học sinh, biết rằng em nào cũng có khả năng làm lớp trưởng và lớp phó?

A. $C_{35}^{2} .$

B. $35^{2} .$

C. $2^{35} .$

D. $A_{35}^{2} .$

Xem đáp án

Câu 37:

Cho tứ diện đều ABCD, M là trung điểm của BC Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng $\frac{\sqrt{3}}{6} ?$

A. $(A M, D M) .$

B. $(A D, D M) .$

C. $(A B, D M) .$

D. $(A B, A M) .$

Xem đáp án

Câu 38:

Có bao nhiêu giá trị nguyên của tham số m trong [-2020;2020] để phương trình $\log (m x) = 2 \log (x + 1)$ có nghiệm duy nhất?

A. 2020

B. 4040

C. 2021

D. 4041

Xem đáp án

Câu 39:

Cho hàm số y = f(x) có đạo hàm liên tục trên R Biết hàm số y = f’(x) có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên để hàm số $g (x) = f (x + m)$ nghịch biến trên khoảng (1;2) Hỏi S có bao nhiêu phần tử?

A. 2020

B. 2021

D. 2022

D. 2019

Xem đáp án

Câu 40:

Ông X muốn xây một bình chứa hình trụ có thể tích $72 m^{3} .$ Đáy làm bằng bê tông giá 100 nghìn đồng/m², thành làm bằng tôn giá 90 nghìn đồng/m², nắp bằng nhôm giá 140 nghìn đồng/m². Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

A. $\frac{\sqrt{3}}{\sqrt[3]{π}} (m) .$

B. $\frac{3}{\sqrt[3]{π}} (m) .$

C. $\frac{2}{\sqrt[3]{π}} (m) .$

D. $\frac{3 \sqrt[3]{3}}{2 \sqrt[3]{π}} (m) .$

Xem đáp án

Câu 41:

Cho hàm số $y = x^{4} - 2 m x^{2} + m,$ có đồ thị (C) với là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến $∆$ với đồ thị (C) tại A cắt đường tròn $(γ) {(x - 1)}^{2} + {(y - 1)}^{2} = 4$ tạo thành một dây cung có độ dài nhỏ nhất.

A. $- \frac{15}{16} .$

B. $\frac{15}{16} .$

C. $- \frac{17}{16} .$

D. $\frac{17}{16} .$

Xem đáp án

Câu 42:

Gọi (S) là tập hợp các giá trị nguyên m để đồ thị hàm số $y = |3 x^{4} - 8 x^{3} - 6 x^{2} + 24 x - m|$ có 7 điểm cực trị. Tính tổng các phần tử của S

A. 42

B. 30

C. 50

D. 63

Xem đáp án

Câu 43:

Cho hàm số y =f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số $g (x) = f (4 x - x^{2}) + \frac{1}{3} x^{3} - 3 x^{2} + 8 x - \frac{5}{3}$ trên đoạn [1;3]

A. 10

B. 9

C. - 10

D. $- \frac{5}{3} .$

Xem đáp án

Câu 44:

Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng 1m và 1,2m Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng tổng thế tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây?

A.1,75m

B.1,56m

C.1,65m

D. 2,12m

Xem đáp án

Câu 45:

Cho hình chóp S.BCD có đáy ABCD hình vuông cạnh a Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp hình chóp là:

A. $\frac{a \sqrt{7}}{3} .$

B. $\frac{a \sqrt{11}}{4} .$

C. $\frac{a \sqrt{21}}{6} .$

D. $\frac{2 a}{3} .$

Xem đáp án

Câu 46:

Cho hình lập phương ABCD.A’B’C’D’ có tâm O Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho MO=2MI Khi đó côsin góc tạo bởi hai mặt phẳng (MC'D’) và (MAB) bằng

A. $\frac{17 \sqrt{13}}{65} .$

B. $\frac{6 \sqrt{85}}{85} .$

C. $\frac{6 \sqrt{13}}{65} .$

D. $\frac{7 \sqrt{85}}{85} .$

Xem đáp án

Câu 47:

Cho đa giác lồi $A_{1} A_{2} ... A_{20} .$ Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho bằng

A. $\frac{24}{57} .$

B. $\frac{40}{57} .$

C. $\frac{27}{57} .$

D. $\frac{28}{57} .$

Xem đáp án

Chọn B.

Mỗi cách chọn ngẫu nhiên 3 đỉnh từ các đỉnh của đa giác sẽ tạo ra một tam giác và số tam giác là $n (Ω) = C_{20}^{3} .$

Gọi là biến cố 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.

Ta có mỗi tam giác thuộc $Ω$ thì có một trong 4 trường hợp sau:

TH1: Cả 3 cạnh của tam giác là các cạnh của đa giác, trường hợp này không có tam giác nào.

TH2: Chỉ có 2 cạnh của tam giác là cạnh của đa giác, khi đó đỉnh chung của 2 cạnh này sẽ là đỉnh của đa giác ban đầu, trường hợp này có 20 tam giác.

TH3: Chỉ có 1 cạnh của tam giác là cạnh của đa giác khi đó ứng với mỗi cạnh bất ký của đa giác thì sẽ có 16 tam giác thỏa mãn, vậy trường hợp này sẽ có 20x16 = 320 tam giác.

TH4: Không có cạnh nào của tam giác là cạnh của đa giác, khi đó tất cả các cạnh của tam giác đều là các đường chéo của đa giác.

Từ đây ta có $n (A) = n (Ω) - 20 - 320 = 800$ tam giác.

Vậy xác suất để chọn được 3 đỉnh tạo thành tam giác không có cạnh nào của đa giác đã cho là $P (A) = \frac{n (A)}{n (Ω)} = \frac{40}{57} .$

Câu 48:

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt A,B,C (B nằm giữa A và C) sao cho AB=2BC Tính tổng các phần tử thuộc

A. -4

B. $\frac{7 - \sqrt{7}}{7} .$

C. -2

D. 0

Xem đáp án

Câu 49:

Cho hình chóp S.ABC có $A B = A C = 4, B C = 2, S A = 4 \sqrt{3}; ∠ S A B = ∠ S A C = 30^{0} .$ Gọi $G_{1}, G_{2}, G_{3}$ lần lượt là trọng tâm của các tam giác $Δ S B C; Δ S C A; Δ S A B$ và T đối xứng S qua mặt phẳng (ABC) Thể tích của khối chóp $T . G_{1} G_{2} G_{3}$ bằng $\frac{a}{b}$ với và $\frac{a}{b}$ tối giản. Tính giá trị P = 2a-b

A. 3

B. 5

C. -9

D. 1

Xem đáp án

Câu 50:

Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V Gọi M,N lần lượt là trung điểm của các cạnh $A B, A' C' . P$ là điểm trên các cạnh BB’ sao cho $P B = 2 P B' .$ Thể tích khối tứ diện CMNP bằng:

A. $\frac{1}{3} V .$

B. $\frac{7}{12} V .$

C. $\frac{5}{12} V .$

D. $\frac{2}{9} V .$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ đề thi Toán THPT Quốc gia năm 2022 có lời giải (30 đề)

Bộ đề thi Toán THPT Quốc gia năm 2022 có lời giải (Đề số 20)

Danh sách câu hỏi

Bài thi liên quan