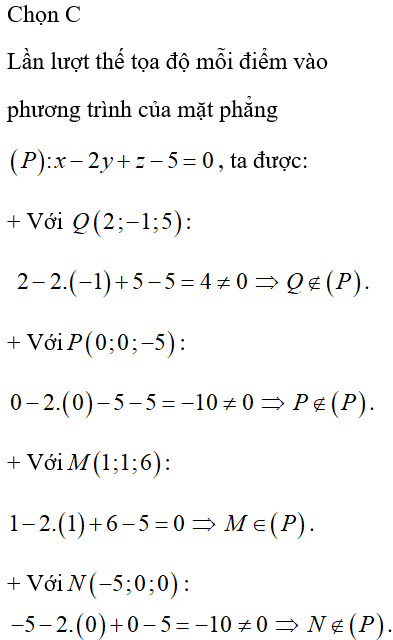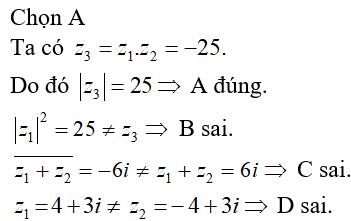[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có lời giải (30 đề)
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có lời giải (Đề số 10)
-
49486 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Khối trụ có bán kính đáy bằng a và chiều cao bằng 2a có thể tích là
 Xem đáp án
Xem đáp án
Chọn B
Thể tích của khối trụ cần tìm là: .
Câu 3:
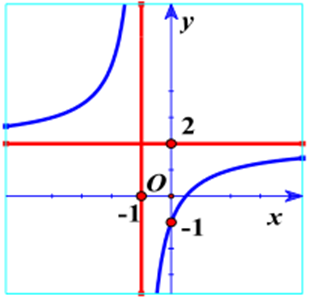
Đường cong trong hình bên là của đồ thị hàm số nào?
 Xem đáp án
Xem đáp án
Chọn C
Vì đồ thị có tiệm cận ngang y=2, tiệm cận đứng x=-1, cắt trục Oy tại (0;-1).
Đáp án A sai vì đồ thị cắt Oy tại (0;1).
Đáp án B sai vì đồ thị có tiệm cận ngang y=1.
Đáp án C sai vì đồ thị có tiệm cận đứng x=1
Câu 5:
Cho véc tơ , tìm véc tơ cùng phương với véc tơ
 Xem đáp án
Xem đáp án
Chọn A
Ta có: , nên . Vậy cùng phương với
Câu 6:
Đường tiệm cận ngang của đồ thị hàm số là đường thẳng
 Xem đáp án
Xem đáp án
Chọn A
Ta có nên đồ thị hàm số có đường tiệm cận ngang là y=2.
Câu 9:
Trong không gian Oxyz, cho mặt phẳng . Véctơ nào sau đây là một véctơ pháp tuyến của (P)
 Xem đáp án
Xem đáp án
Chọn B
. Véctơ là một véctơ pháp tuyến của (P).
Câu 10:
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây
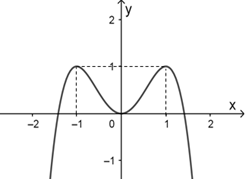
Mệnh đề nào sau đây đúng về hàm số đó?
 Xem đáp án
Xem đáp án
Chọn C
Dựa vào đồ thị ta thấy chỉ có phương án C là đúng
Câu 13:
Trong không gian Oxyz, mặt cầu có tâm và bán kính lần lượt là
 Xem đáp án
Xem đáp án
Chọn D
Mặt cầu có tâm I(-1;3;2) và bán kính R=3.
Câu 14:
Cho n và k là hai số nguyên dương tùy ý thỏa mãn , mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn B
Ta có nên khẳng định A sai.
nên khẳng định D sai.
Với n=4 và k=2, ta có , khẳng định C sai.
. Vậy khẳng định B đúng.
Câu 15:
Một khối nón có bán kính đáy bằng 3cm và đường sinh độ dài 5cm. Thể tích của khối nón đã cho bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta có : r=3, l=5. Vậy chiều cao của khối nón là:
Suy ra thể tích khối nón là:
Câu 16:
Cho hàm số y=f(x) có bảng biến thiên như sau
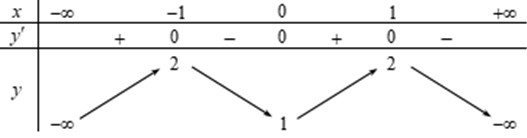
Hàm số đạt cực tiểu tại điểm
 Xem đáp án
Xem đáp án
Chọn D
Từ bảng biến thiên ta thấy hàm số đạt cực tiểu tại x=0
Câu 20:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết cạnh bên SA=2a và vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABCD.
 Xem đáp án
Xem đáp án
Chọn D
Ta có .
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, , tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD.
 Xem đáp án
Xem đáp án
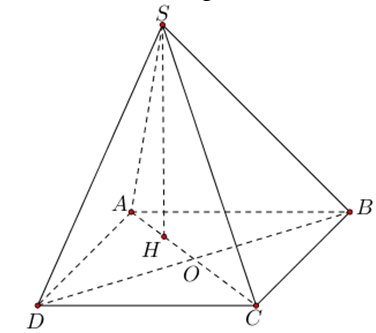
Chọn B
Gọi H là hình chiếu vuông góc của S lên AC.
Ta có suy ra là tam giác đều.
.
Vậy .
Câu 22:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng
 Xem đáp án
Xem đáp án
Chọn B
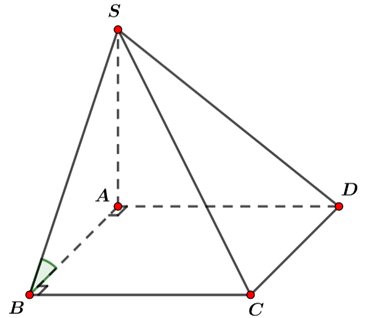
Ta có ,mà
Tam giác SAB vuông tại A nên góc nhọn nên .
Trong tam giác vuông SAB:
Câu 23:
Ba số theo thứ tự lập thành một cấp số nhân. Công bội của cấp số nhân này bằng
 Xem đáp án
Xem đáp án
Chọn B
Ba số theo thứ tự lập thành một cấp số nhân nên .
Ba số đó lần lượt là ; ; . Công bội của cấp số nhân này bằng .
Câu 24:
Tìm tập nghiệm S của bất phương trình
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
Vậy bất phương trình có tập nghiệm là
Câu 25:
Gọi lượt là hoành độ giao điểm của hai đồ thị hàm số và . Tính
 Xem đáp án
Xem đáp án
Chọn D
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:
+ Ta có:
+
Câu 26:
Một bình đựng 5 viên bi xanh và 4 viên bi đỏ. Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được 2 viên bi cùng màu
 Xem đáp án
Xem đáp án
Chọn A
Gọi A là biến cố “Chọn được 2 viên bi cùng màu”, B là biến cố “Chọn được 2 viên bi màu xanh”, C là biến cố “Chọn được 2 viên bi màu đỏ”, khi đó và hai biến cố và xung khắc.
Ta có: .
Câu 27:
Hàm số f(x) có đạo hàm Số điểm cực trị của hàm số f(x) là
 Xem đáp án
Xem đáp án
Chọn A
Dấu của f'(x)

Từ kết quả xét dấu f'(x) suy ra hàm số chỉ có 2 điểm cực trị là x=0;x=1.
Câu 28:
Cho hàm số có một nguyên hàm là F(x). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn D
Ta có .
F(2)=F(0)=4.
Câu 29:
Cho hàm số y=f(x) có . Hàm số y=f(x) đồng biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
.
.
Bảng biến thiên
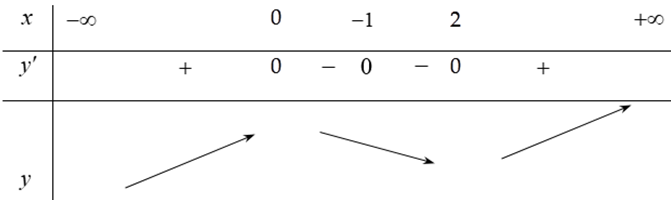
Từ bảng biến thiên ta chọn đáp án D.
Câu 31:
Trong không gian Oxyz, cho các điểm I(1;0;-1), A(2;2;-3). Mặt cầu (S) tâm I và đi qua điểm A có phương trình là:
 Xem đáp án
Xem đáp án
Chọn A
Mặt cầu (S) tâm I và đi qua điểm A có bán kính .
Phương trình mặt cầu (S): .
Câu 32:
Tìm giá trị nhỏ nhất m của hàm số trên đoạn [-2;3]
 Xem đáp án
Xem đáp án
Chọn A
Hàm số xác định và liên tục trên đoạn [-2;3].
; .
f(-3)=25; f(0)=13; ; ; f(3)=85.
Vậy giá trị nhỏ nhất .
Câu 34:
Cho số phức với . Tìm a để điểm biểu diễn của số phức nằm trên đường phân giác của góc phần tư thứ hai và thứ tư.
 Xem đáp án
Xem đáp án
Chọn D
Đường phân giác của góc phần tư thứ hai và thứ tư là đường thẳng y=-x.
Do đó a-5=-a. Suy ra .
Câu 37:
Trong không gian Oxyz cho điểm A(1;-2;3) và hai đường thẳng . Viết phương trình đường thẳng đi qua A, vuông góc với cả và
 Xem đáp án
Xem đáp án
Chọn A
Đường thẳng có véctơ chỉ phương ; có véctơ chỉ phương .
Ta có: .
Vì đường thẳng đi qua A, vuông góc với cả và nên nhận làm véctơ chỉ phương, do đó có phương trình là
Câu 38:
Cho hình chóp S.ABC có tam giác ABC là tam giác vuông tại A, , . Góc giữa SC và mặt phẳng (ABC) bằng . Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến (SBC) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn C
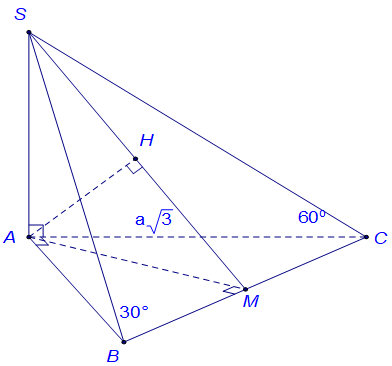
Dựng ;
Ta có: và
Tam giác SAC vuông tại A =
Tam giác ABC vuông tại A
Tam giác SAM vuông tại A
Câu 39:
Thể tích V của khối hộp chữ nhật ABCD.A'B'C'D' biết là
 Xem đáp án
Xem đáp án
Chọn C
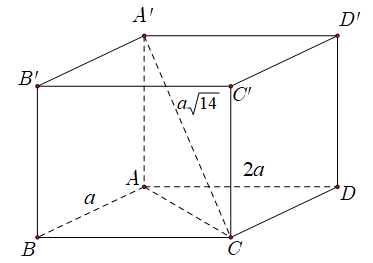
Xét hình chữ nhật ABCD, ta có
Xét tam giác vuông AA'C ta có
Ta có
Câu 40:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và hai đường thẳng , . Phương trình đường thẳng đi qua A, vuông góc với và cắt là
 Xem đáp án
Xem đáp án
Chọn D
Đường thẳng có VTCP .
Giả sử (P) là mặt phẳng qua A và vuông góc với
Gọi B là giao điểm của (P) và . Tọa độ B là nghiệm của hệ phương trình:
.
Đường thẳng cần tìm là đường thẳng
Ta có hay VTCP của đường thẳng cần tìm là
Đường thẳng cần tìm đi qua B(1;2;0) và có VTCP là
Suy ra phương trình đường thẳng cần tìm: .
Cách 2: (AD: Nguyễn Văn Thịnh)
Gọi là đường thẳng cần tìm. cắt tại B.
Ta có .
Đường thẳng có vectơ chỉ phương là , có vectơ chỉ phương là .
Ta có . Suy ra .
Đường thẳng cần tìm đi qua B(1;2;0) và có VTCP là
Suy ra phương trình đường thẳng cần tìm: .
Câu 41:
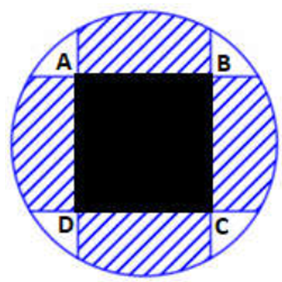
Bồn hoa của một trường X có dạng hình tròn bán kính bằng 8m. Người ta chia bồn hoa thành các phần như hình vẽ dưới đây và có ý định trồng hoa như sau: Phần diện tích bên trong hình vuông để trồng hoa. Phần diện tích kéo dài từ 4 cạnh của hình vuông đến đường tròn dùng để trồng cỏ. Ở 4 góc còn lại mỗi góc trồng một cây cọ. Biết AB=4m, giá trồng hoa là 200.000 đ/m2, giá trồng cỏ là 100.000 đ/m2, mỗi cây cọ giá 150.000 đ. hỏi cần bao nhiêu tiền để thực hiện việc trang trí bồn hoa đó
 Xem đáp án
Xem đáp án
Chọn A
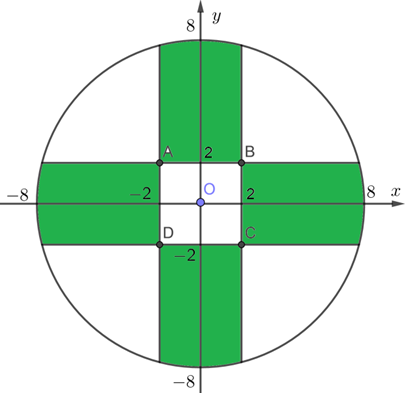
Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với tâm hình tròn, suy ra phương trình
đường tròn là: .
+ Diện tích hình vuông ABCD là: .
Số tiền để trồng hoa là: .
+ Diện tích trồng cỏ là: .
Số tiền trồng cỏ là: .
+ Số tiền trồng 4 cây cọ là: .
Vậy tổng số tiền để thực hiện việc trang trí bồn hoa là:
.
Câu 42:
Giả sử hàm số f(x) có đạo hàm cấp 2 trên thỏa mãn và với mọi . Tính tích phân
 Xem đáp án
Xem đáp án
Chọn A
Đặt .
Suy ra .
Do .
Vậy .
Đặt t=1-x suy ra .
Đặt
Suy ra .
Câu 43:
Cho hàm số f(x) có đồ thị f'(x) như hình vẽ dưới. Hàm số có bao nhiêu điểm cực trị?
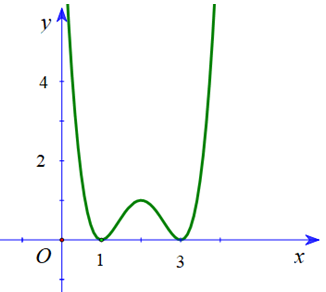
 Xem đáp án
Xem đáp án
Chọn C
Có
Ta có đồ thị hàm số và đồ thị hàm y=f'(x) như hình vẽ dưới
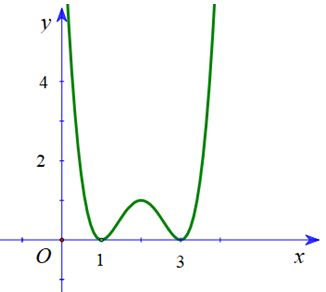
Quan sát hình vẽ ta thấy có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn
Vậy hàm số g(x) có 2 điểm cực trị.
Câu 44:
Cho hàm số y=f(x) liên tục trên đoạn . Biết và . Tính tích phân .
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
Lấy nguyên hàm hai vế ta được: theo đề bài ta có
suy ra .
Câu 45:
Bất phương trình nghiệm đúng với mọi . Tập tất cả cá giá trị của m là
 Xem đáp án
Xem đáp án
Chọn C
Bất phương trình .
Đặt bất phương trình trở thành .
Bất phương trình (1) nghiệm đúng với mọi khi và chỉ khi bất phương trình (2) nghiệm đúng với mọi .
(do ).
Đặt với .
.
Bảng biến thiên
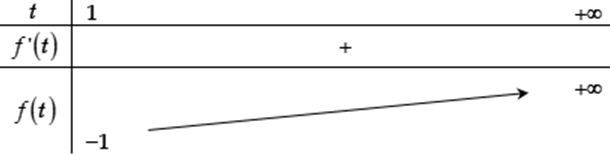
Từ bảng biến thiên ta có .
Câu 46:
Cho hàm số y=f(x) có đạo hàm liên tục trên . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích hình phẳng (K),(H) lần lượt là và . Biết . Tính f(2)
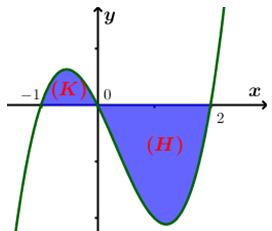
 Xem đáp án
Xem đáp án
Chọn C
Từ hình vẽ ta có: , suy ra
Ta cũng có: , suy ra .
Câu 47:
Cho số phức z thỏa mãn . Giá trị lớn nhất của biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn C
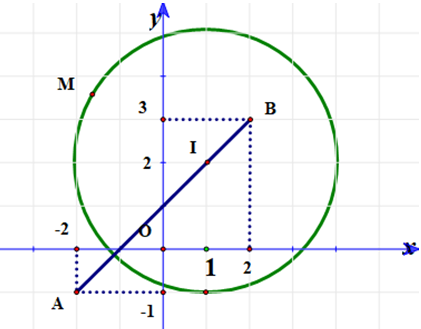
.
Gọi , là vec-tơ biểu diễn cho các số phức , .
Từ (1) có .
Suy ra M thuộc đường tròn (C) tâm I(1;2) bán kính R=3,
Gọi , lần lượt là vec-tơ biểu diễn cho số phức , .
Có , . Suy ra .
Lúc đó .
Có .
Có , , , nên .
Suy ra .
Có .
Vậy giá trị lớn nhất của P là .
Câu 48:
Trong không gian Oxyz, cho ba điểm A(2;-2;4), B(-3;3;-1), C(-1;-1;-1) và mặt phẳng . Xét điểm M thay đổi thuộc (P), tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Chọn C
Gọi I là điểm thỏa mãn:
.
Khi đó, với mọi điểm , ta luôn có:
.
Ta tính được .
Do đó, T đạt GTNN đạt GTNN .
Lúc này, .
Vậy .
Câu 49:
Gọi S là tập hợp tất cả các giá trị của tham số và phương trình có nghiệm duy nhất. Tìm số phần tử của S.
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện
Giải phương trình
Khi Suy ra phương trình (1) vô nghiệm
Khi không có x thỏa điều kiện.
Khi khi đó
TH1. Phương trình (1) có nghiệm duy nhất x=2 khi đó
TH2. Phương trình có nghiệm duy nhất khi đó
Vậy các giá trị m thỏa mãn điều kiện đề bài là
Vậy .
Câu 50:
Cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ sau
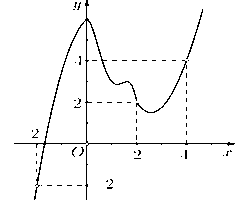
Đồ thị hàm số có tối đa bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn A
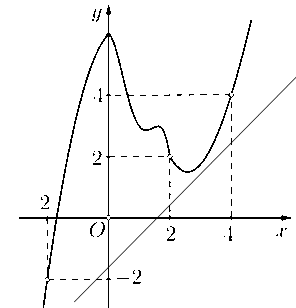
Xét hàm số
Từ đồ thị ta thấy
Bảng biến thiên
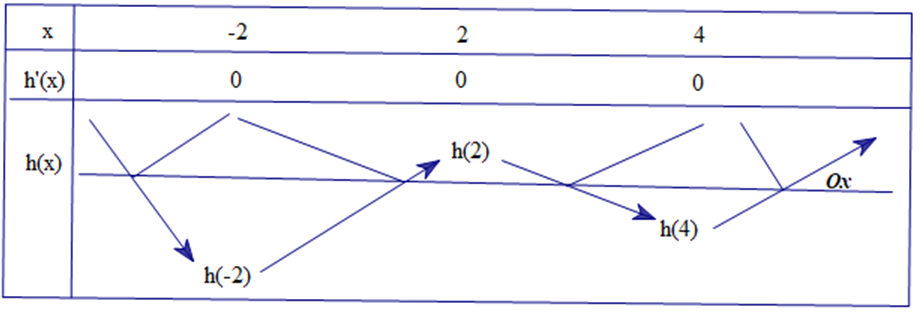
Vậy có tối đa 7 cực trị.