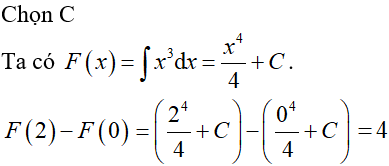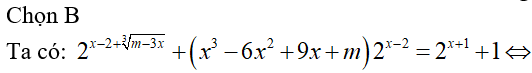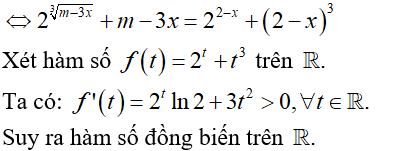[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có lời giải (30 đề)
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có lời giải (Đề số 11)
-
49479 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
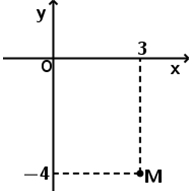
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn C
Điểm nên M là điểm biểu diễn của số phức 3-4i
Câu 5:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và thể tích của khối chóp đó bằng . Tính cạnh bên SA.
 Xem đáp án
Xem đáp án
Chọn D
.
Câu 6:
Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Diên tích xung quanh của hình trụ bằng
 Xem đáp án
Xem đáp án
Chọn A
Diện tích xung quanh của hình trụ là
Câu 7:
Cho tập hợp A có 20 phần tử, số tập con có hai phần tử của A là
 Xem đáp án
Xem đáp án
Chọn C
Mỗi tập con có hai phần tử của A tương ứng với một tổ hợp chập 2 của 20 phần tử
Vậy số tập con có hai phần tử của A là
Câu 8:
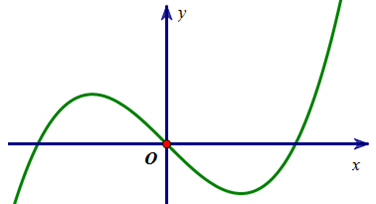
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
 Xem đáp án
Xem đáp án
Chọn C
+ Đồ thị hàm số có hệ số a>0 nên loại đáp án B và C
+ Đồ thị hàm số đi qua gốc tọa độ nên loại đáp án A.
Câu 9:
Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a. Diện tích xung quanh của hình nón đó bằng
 Xem đáp án
Xem đáp án
Chọn B
Diện tích xung quanh của hình nón: .
Câu 10:
Cho . Tìm số phức nghịch đảo của số phức z
 Xem đáp án
Xem đáp án
Chọn B
Ta có: .
Vậy số phức nghịch đảo của số phức là .
Câu 13:
Cho hàm số f(x) có bảng biến thiên như sau
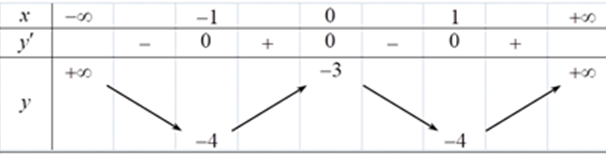
Hàm số đạt cực đại tại bằng
 Xem đáp án
Xem đáp án
Chọn A
Từ bảng biến thiên Hàm số đạt cực đại tại
Câu 15:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: . Mặt cầu (S) có tâm I bán kính R là
 Xem đáp án
Xem đáp án
Chọn B
Ta có
Mặt cầu có tâm (S) và bán kính
Câu 16:
Trong không gian Oxyz, điểm nào dưới đây thuộc trục Oz?
 Xem đáp án
Xem đáp án
Chọn C
Điểm thuộc trục Oz là: .
Câu 17:
Trong không gian Oxyz, điểm nào dưới đây thuộc trục Oz?
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào bảng biến thiên của hàm số y=f(x) ta thấy hàm số nghịch biến trên các khoảng và (0;1).
Câu 18:
Tìm tọa độ giao điểm của đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số .
 Xem đáp án
Xem đáp án
Chọn D
Tiệm cận đứng: x=-2
Tiệm cận ngang: y=1
Vậy giao điểm là I(-2;1)
Câu 20:
Trong không gian với hệ tọa độ Oxyz, đường thẳng nào sau đây nhận là một vectơ chỉ phương?
 Xem đáp án
Xem đáp án
Chọn A
Xét đường thẳng được cho ở câu C, có một vectơ chỉ phương là (thỏa đề bài).
Câu 23:
Cho hàm số f(x) xác định, liên tục trên f'(x) có bảng xét dấu như sau:
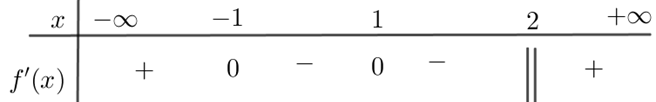
Hàm số f(x) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào BBT và áp dụng định lí 1 của SGK, hàm số đạt cực đại tại x=-1, đạt cực tiêu tại x=2. Suy ra hàm số có 2 điểm cực trị.
Câu 25:
Trong không gian Oxyz, cho hai điểm A(-2;1;0), B(2;-1;2). Phương trình của mặt cầu có đường kính AB là
 Xem đáp án
Xem đáp án
Chọn D
Gọi I là trung điểm của AB khi đó .
.
Mặt cầu đường kính AB nhận điểm làm tâm I(0;0;1) và bán kính có phương trình là: .
Câu 26:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và đường thẳng . Phương trình tham số của đường thẳng đi qua , vuông góc với d và nằm trong (P) là:
 Xem đáp án
Xem đáp án
Chọn B
. Do đó một vectơ chỉ phương của đường thẳng là
Câu 29:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có AB=a, . Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a thể tích của khối chóp S.ABC.
 Xem đáp án
Xem đáp án
Chọn C
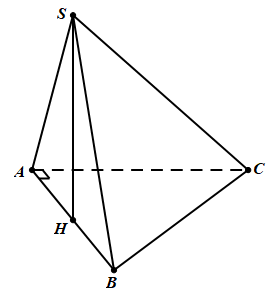
Xét tam giác ABC vuông tại A, ta có: AC=.
Diện tích tam giác ABC là: .
Gọi H là trung điểm đoạn AB thì . Vì và nên . Suy ra SH là chiều cao của khối chóp S.ABC.
Tam giác SAH vuông tại H nên SH.
Thể tích khối chóp S.ABC là:V .
Câu 31:
Biết rằng đồ thị hàm số chỉ cắt đường thẳng y=-3x+4 tại một điểm duy nhất M=a+b. Tổng a+b bằng
 Xem đáp án
Xem đáp án
Chọn B
Xét phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng y=-3x+4 là:
Thay vào y=-3x+4 ta được
Nên đồ thị hàm số cắt đường thẳng y=-3x+4 tại điểm .
Tổng a+b=3.
Câu 33:
Tìm khoảng đồng biến của hàm số .
 Xem đáp án
Xem đáp án
Chọn A
Tập xác định: .
Ta có: .
Bảng biến thiên
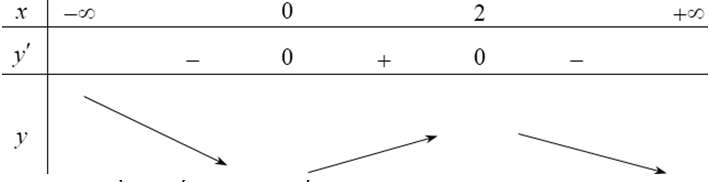
Từ bảng trên ta có khoảng đồng biến của hàm số đã cho là (0;2).
Câu 34:
Cho số thực x thỏa mãn là các số thực dương). Hãy biểu diễn x theo ?
 Xem đáp án
Xem đáp án
Chọn C
Với a,b,c là các số thực dương, ta có
.
Do đó, .
Câu 35:
Tìm giá trị nhỏ nhất của hàm số
 Xem đáp án
Xem đáp án
Chọn B
TXĐ: D=R.
Đặt sinx=t,
Ta có liên tục trên đoạn [-1;1]
f(-1)=-1; ; .
Suy ra , .
Câu 37:
Cho hình chóp S.ABC có và , gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
 Xem đáp án
Xem đáp án
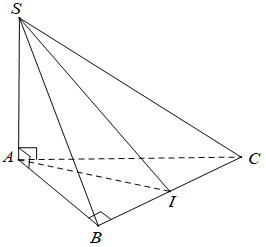
Chọn D
Ta có:
.
Câu 38:
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và . Khoảng cách từ S đến mặt phẳng (ABC) bằng
 Xem đáp án
Xem đáp án
Chọn C
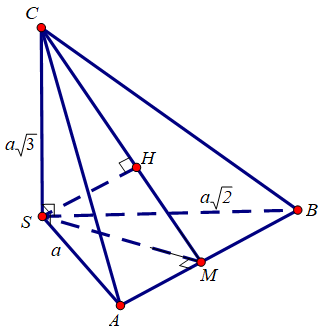
Trong mặt phẳng (SAB), kẻ , suy ra
Trong mặt phẳng (SCM) kẻ (1), . Từ trên ta có (2)
Từ (1) và (2) suy ra .
Tam giác SAB vuông tại S suy ra .
Tam giác SAB vuông tại S suy ra .
Câu 39:
Cho hàm số y=f(x) với f(0)=f(1)=1 Biết rằng: Giá trị biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Lại có
Thế (2) vào (1) ta được . Suy ra nên a+b=0.
Câu 40:
Trong không gian với hệ trục Oxyz, đường vuông góc chung của hai đường thẳng chéo nhau và có phương trình
 Xem đáp án
Xem đáp án
Chọn D
Gọi là đường thẳng cần tìm.
Gọi
Ta có: .
Gọi lần lượt là véc tơ chỉ phương của ta có:
.Chọn .
Vì đều là véc tơ chỉ phương của nên ta có:
.
.
Câu 41:
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
.(*)
Đặt . Bất phương trình (*) trở thành: .
Xét hàm số .
Ta có: (nhận)
Bảng biến thiên
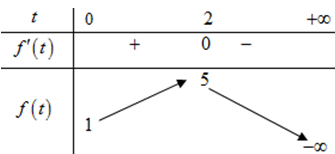
Bất phương trình có nghiệm có nghiệm .
Mà m nguyên dương .
Câu 42:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A, , biết góc giữa B'C và mặt phẳng bằng thỏa mãn . Cho khoảng cách giữa hai đường thẳng A'B và CC' bằng . Tính thể tích V của khối lăng trụ .
 Xem đáp án
Xem đáp án
Chọn B
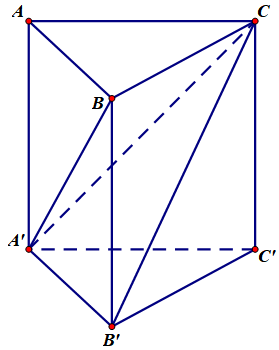
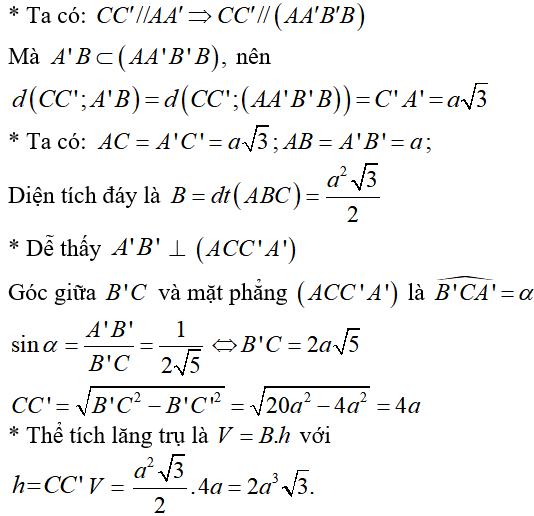
Câu 43:
Cho hàm số f(x) có đạo hàm liên tục trên . Biết f(5)=1 và , khi đó bằng
 Xem đáp án
Xem đáp án
Chọn D
+) .
.
.
+) Ta có: .
Đặt 5x=t.
Vậy .
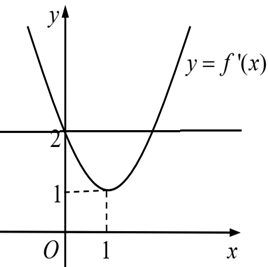
Câu 45:
Cho hàm số y=f(x) có đạo hàm liên tục trên và đồ thị hàm số y=f'(x) là parabol như hình bên dưới.
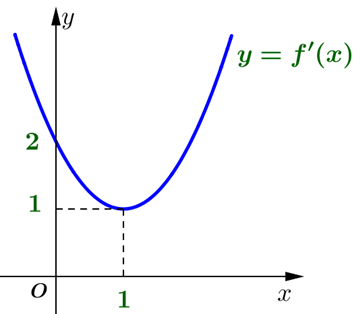
Hàm số có bao nhiêu cực trị?
 Xem đáp án
Xem đáp án
Chọn D
Ta có .
.
Dựa vào đồ thị y=f'(x) và đường thẳng y=2, ta có bảng biến thiên sau
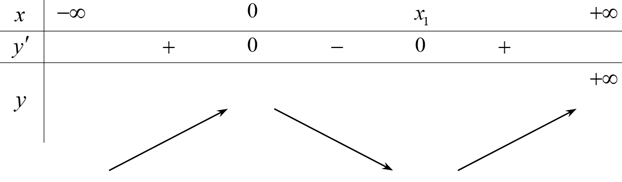
Vậy hàm số có hai điểm cực trị.
Câu 46:
Cho (H) là hình phẳng giới hạn bởi parabol , tiếp tuyến với (P) tại điểm M(2;4) và trục hoành. Tính diện tích của hình phẳng (H)?
 Xem đáp án
Xem đáp án
Chọn A
Ta có .
Tiếp tuyến d với (P) tại điểm M(2;4) có phương trình là:
Giao điểm của d và Ox là A(0;1)
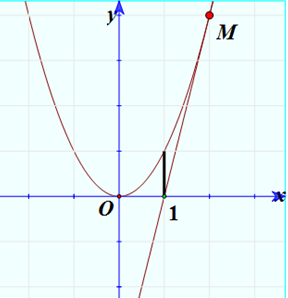
Trên đoạn [0;1] hình phẳng được giới hạn bởi đồ thị hàm số và trục hoành.
Trên đoạn [1;2] hình phẳng được giới hạn bởi đồ thị hàm số và tiếp tuyến d.
Vậy diện tích của hình phẳng được xác định là:
Câu 47:
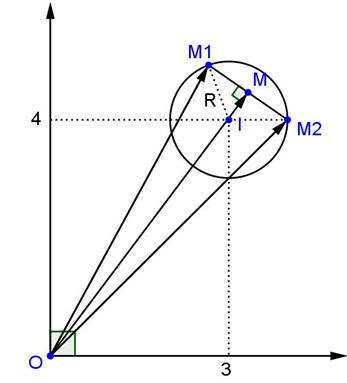
Cho là nghiệm phương trình và thỏa mãn . Giá trị lớn nhất của bằng
 Xem đáp án
Xem đáp án
Chọn B
Gọi , với .
Do
Gọi , .
Mà là nghiệm phương trình
đường tròn .
Tương tự .
Đường tròn (C) có tâm I(3;4), bán kính R=1.
Goị là trung điểm M, , và .
Mà , dấu bằng xảy ra khi O,I,M thẳng hàng. Khi đó , và .
đạt giá trị lớn nhất bằng 2(OI+IM), bằng .
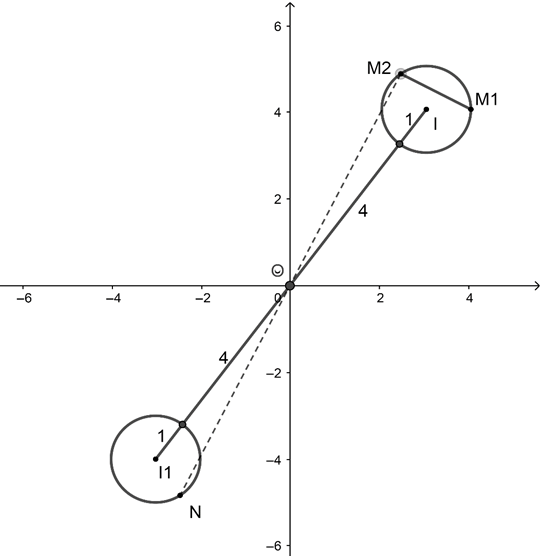
Hoặc đánh giá chọn đáp án như sau:
Gọi
Và N đối xứng với qua gốc tọa độ O, đường tròn .
có tâm , bán kính , đối xứng với (C) qua gốc tọa độ O.
Có .
Nhận xét: với mọi điểm , thì . Loại các đáp án B,C,D
đạt giá trị lớn nhất bằng .
Câu 48:
Cho hàm số . Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có đúng điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
TH1: m=1
hoành độ của đỉnh là 1 số dương nên có điểm cực trị
Vậy thỏa mãn nhận m=1.
TH2:
Để hàm số có điểm cực trị thì có 2 nghiệm phân biệt và thỏa hoặc .
_ .
_ .
Kết hợp 2 trường hợp ta được có 4 giá trị nguyên của tham số m.
Câu 49:
Trong không gian Oxyz, cho các điểm A(0;0;2) và B(3;4;1). Gọi (P) là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu với . M, N là hai điểm thuộc (P) sao cho MN=1. Giá trị nhỏ nhất của AM+BN là
 Xem đáp án
Xem đáp án
Chọn C
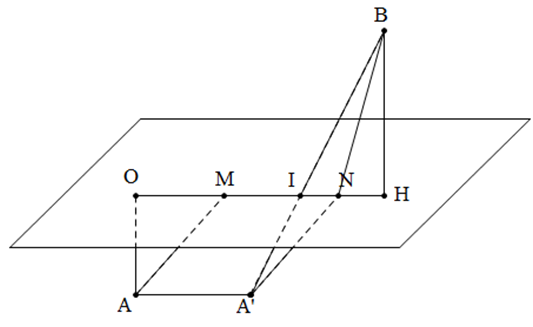
Từ
Lấy (1) trừ (2), ta được 6z=0 hay
tức là
Dễ thấy A, B nằm khác phía đối với (P), hình chiếu của A trên (P) là O, hình chiếu của B trên (P) là
Lấy A' sao cho
Khi đó và cực trị chỉ xảy ra khi cùng phương
Lấy
Khi đó vì nên Do đó