Trắc nghiệm bài tập theo tuần Toán 7-Tuần 15 có đáp án
-
6322 lượt thi
-
11 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 3:
|
x |
|
|
|
0 |
|
|
|
y |
|
|
|
|
|
3 |
 Xem đáp án
Xem đáp án
Điền các giá trị tương ứng của hàm số vào bảng :
|
x |
|
-1 |
|
0 |
2,7 |
|
|
y |
|
|
|
0 |
|
3 |
Câu 5:
Hàm số được cho bởi công thức
Tìm x biết
 Xem đáp án
Xem đáp án
TH1:
TH2:
(vô lí)
Không tồn tại x sao cho
Câu 6:
Hàm số được cho bởi công thức
Hãy điền các giá trị tương ứng của hàm số vào bảng sau:
|
x |
-2 |
-1 |
|
0 |
|
2 |
|
|
|
0 |
|
3 |
|
 Xem đáp án
Xem đáp án
|
x |
-2 |
-1 |
|
0 |
1 |
2 |
|
|
-3 |
-1 |
0 |
1 |
3 |
5 |
Câu 7:
Hàm số được cho bởi công thức
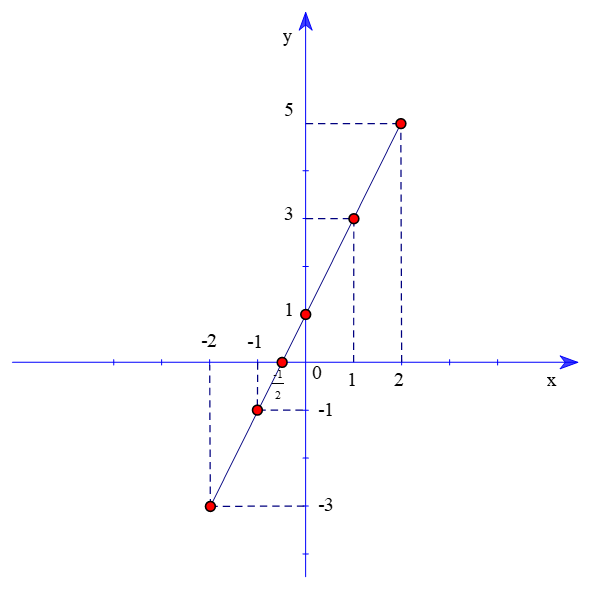
Vẽ hệ trục tọa độ Oxy và đánh dấu tất cả các điểm (x;y) ở bảng trên. Em có nhận xét gì về vị trí của 6 điểm đó.
 Xem đáp án
Xem đáp án
Nhận xét : 6 điểm trên cùng nằm trên một đường thẳng.
Câu 8:
Cho tam giác ABC. Trên nửa mặt phẳng chứa điểm A bờ là đường thẳng BC vẽ tia . Lấy điểm sao cho Đường thẳng qua vuông góc với BC và đường thẳng qua C vuông góc với BD cắt nhau tại P. Chứng minh
 Xem đáp án
Xem đáp án
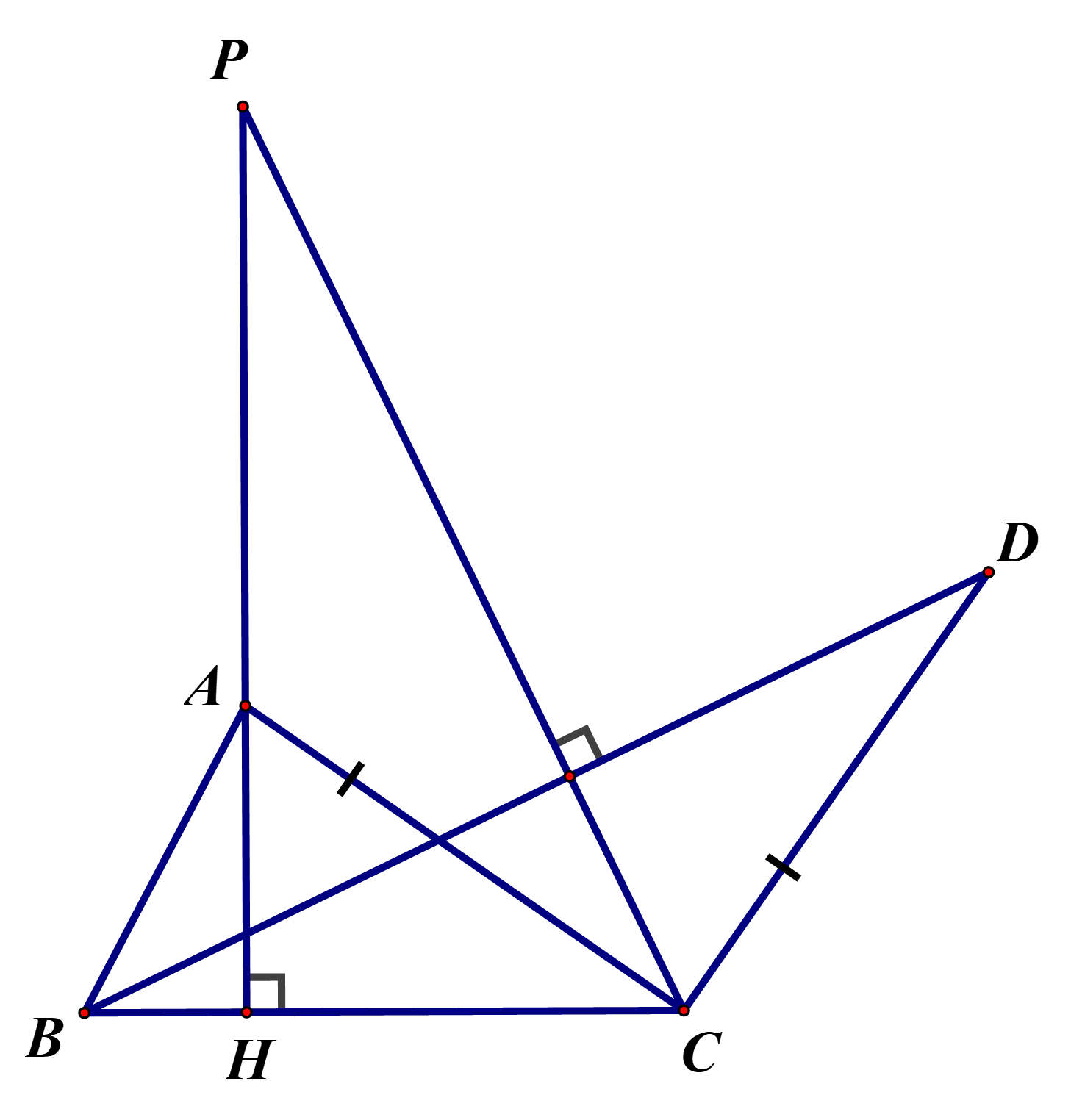
Ta có:
(hai góc phụ nhau)
Vì (hai góc phụ nhau)
Mà
hay
Mà (2 góc kề bù)
Xét và có:
(2 cạnh tương ứng)
Câu 9:
Cho góc Oxy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot kẻ đường vuông góc với Ot nó cắt Ox và Oy theo thứ tự A và B
Chứng minh OA=OB
 Xem đáp án
Xem đáp án
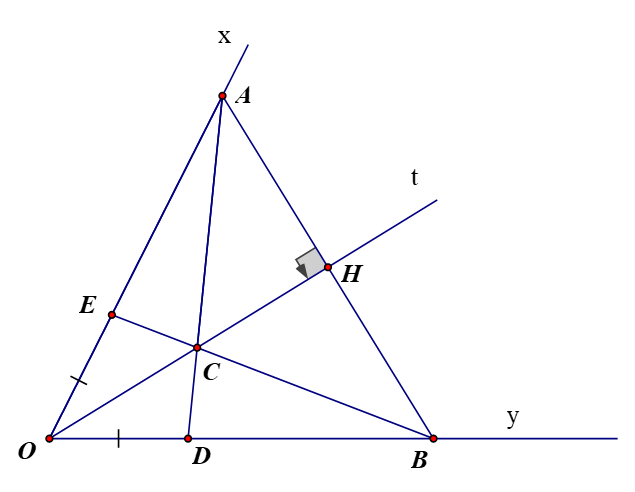
Xét và có
OH là cạnh chung
(OH là tia phân giác)
(2 cạnh tương ứng)
Câu 10:
Cho góc Oxy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot kẻ đường vuông góc với Ot nó cắt Ox và Oy theo thứ tự A và B
 Xem đáp án
Xem đáp án
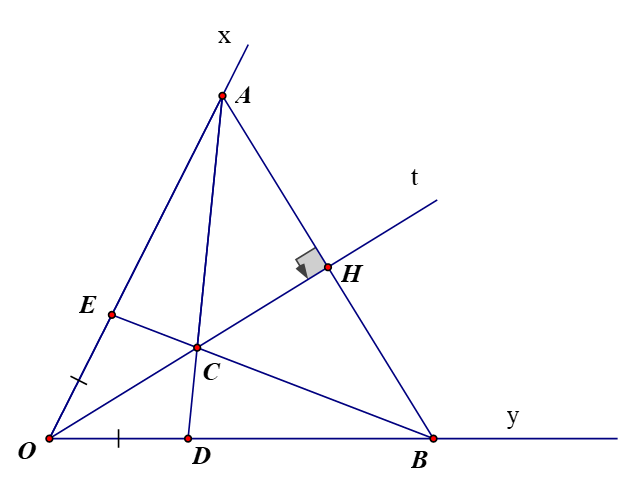
Ta có (cmt)
(2 cạnh tương ứng)
Xét và có:
(2 cạnh tương ứng)
Câu 11:
AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE=OD. Chứng minh thẳng hàng.
 Xem đáp án
Xem đáp án
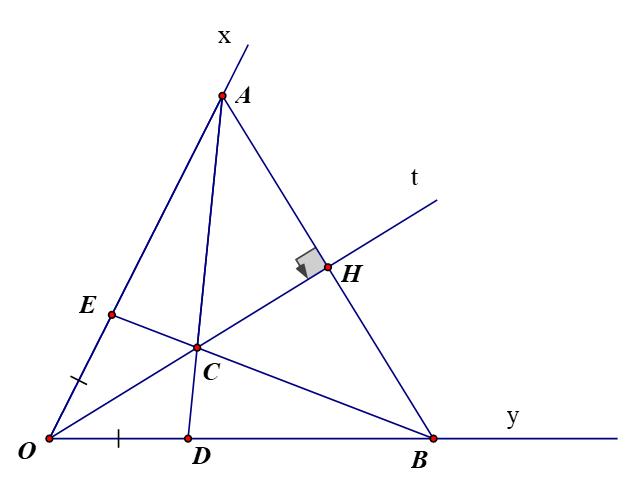
Ta có
Mà
Xét và có:
(gt)
(OH là tia phân giác)
OC chung
(2 cạnh tương ứng)
Xét và có:
( 2 góc tương ứng)
Mặt khác (AC cắt Oy tại D)
thẳng hàng (đpcm)
