Trắc nghiệm bài tập theo tuần Toán 7-Tuần 16 có đáp án
-
6335 lượt thi
-
11 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Vẽ đồ thị hàm số
 Xem đáp án
Xem đáp án
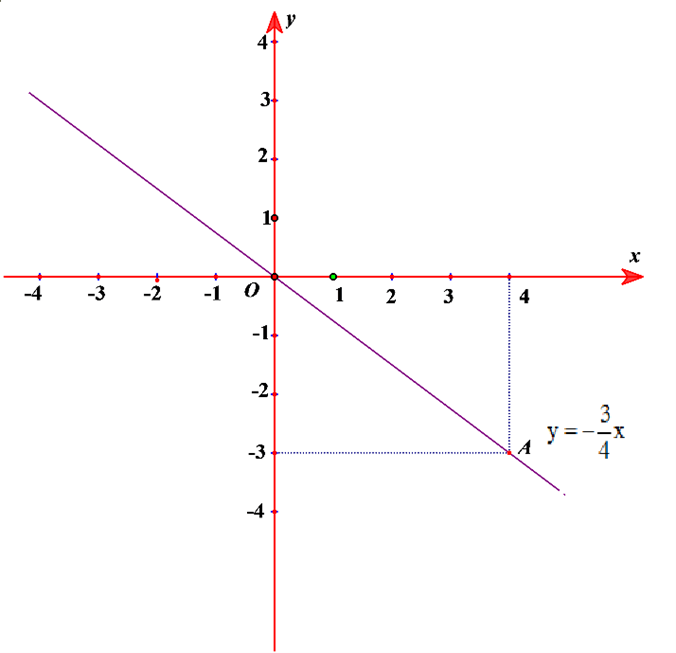
Vẽ hệ trục tọa độ Oxy.
Bảng giá trị:
|
x |
0 |
4 |
|
|
0 |
|
Điểm thuộc đồ thị hàm số . Vậy đường thẳng là đồ thị của hàm số đã cho.
Câu 2:
Bằng phép tính hãy xác định xem điểm nào thuộc đồ thị hàm số và biễu diễn điểm đó trên mặt phẳng tọa độ.
 Xem đáp án
Xem đáp án
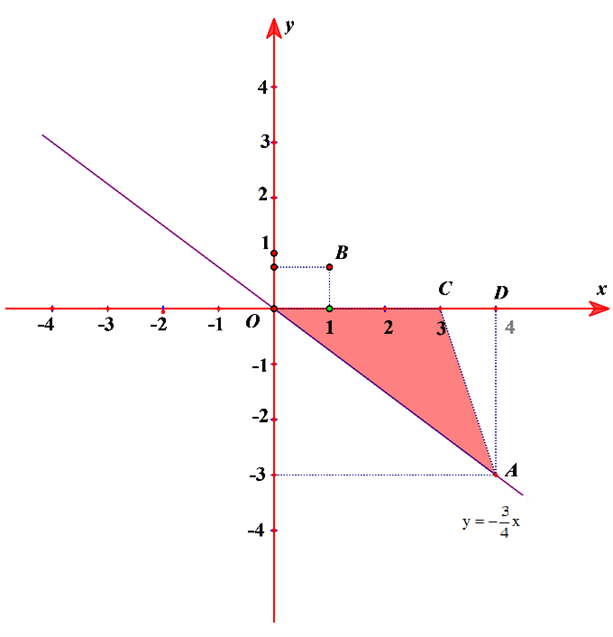
+) Thế vào hàm số , ta được bằng tung độ điểm A
Vậy thuộc đồ thị hàm số
+) Thế vào hàm số , ta được: khác tung độ điểm B.
Vậy không thuộc đồ thị hàm số
+) Thế vào hàm số , ta được:
khác tung độ điểm C.
Vậy không thuộc đồ thị hàm số .
Câu 4:
Xác định hệ số a biết đồ thị hàm số đi qua điểm và vẽ đồ thị của hàm số trên.a
 Xem đáp án
Xem đáp án
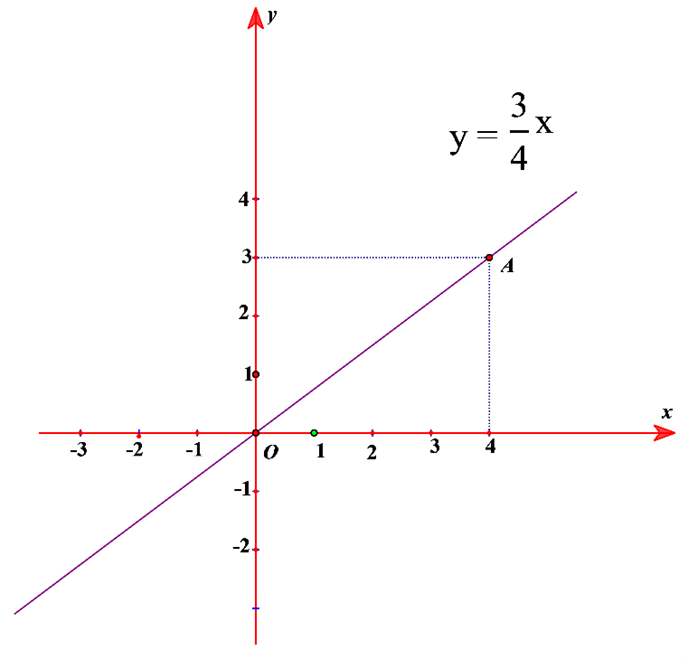
Đồ thị hàm số đi qua điểm
+) Vẽ đồ thị hàm số .
Vẽ hệ trục tọa độ .
Bảng giá trị:
|
x |
0 |
4 |
|
|
0 |
3 |
Điểm thuộc đồ thị hàm số .
Vậy đường thẳng là đồ thị của hàm số đã cho.
Câu 5:
Những điểm nào sau đây thuộc đồ thị hàm số trên:
 Xem đáp án
Xem đáp án
- Thế vào hàm số , ta được: bằng tung độ điểm B.
Vậy thuộc đồ thị hàm số .
- Thế vào hàm số , ta được: bằng tung độ điểm C.
Vậy thuộc đồ thị hàm số .
- Thế vào hàm số , ta được: bằng tung độ điểm D .
Vậy thuộc đồ thị hàm số
Câu 6:
Biết điểm ; thuộc đồ thị hàm số trên. Tính giá trị của
 Xem đáp án
Xem đáp án
- Điểm thuộc đồ thị hàm số
- Điểm thuộc đồ thị hàm số
Câu 7:
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A,C. Trên tia Oy lấy hai điểm B,D sao cho
Chứng minh: AD=BC
 Xem đáp án
Xem đáp án
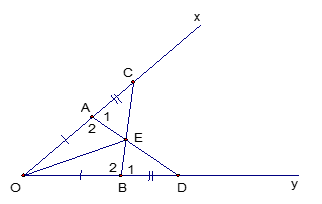
và có:
(gt)
là góc chung
(gt)
Vậy (c.g.c)
(2 cạnh tương ứng)
Câu 8:
 Xem đáp án
Xem đáp án
(kề bù); (kề bù)
Mà (vì ) nên
* Xét và có:
(suy ra từ giả thiết)
(theo chứng minh trên)
(vì )
Vậy (g.c.g)
(2 cạnh tương ứng của hai tam giác bằng nhau)
* Xét và có:
(gt)
là cạnh chung
(theo chứng minh trên)
Vậy và (c.c.c)
(2 góc tương ứng của hai tam giác bằng nhau)
Hay OE là phân giác của góc xOy (đpcm).
Câu 9:
Cho tam giác ABC có các góc đều nhọn, và AB<AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
Chứng minh AB=AF Xem đáp án
Xem đáp án
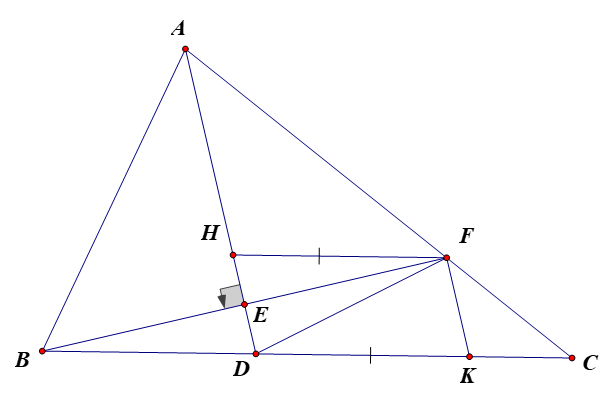
(g-c-g)
suy ra
Câu 10:
 Xem đáp án
Xem đáp án
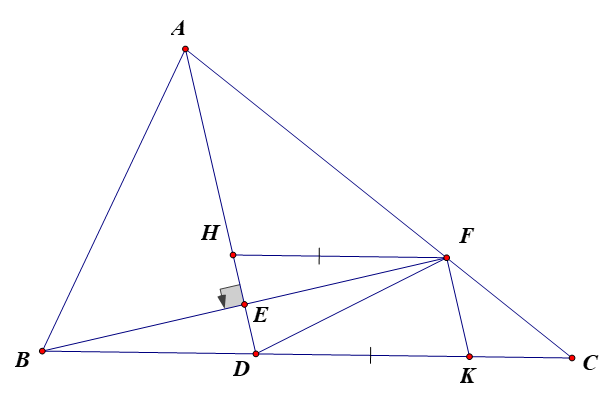
(c-g-c)
suy ra ;
Câu 11:
 Xem đáp án
Xem đáp án
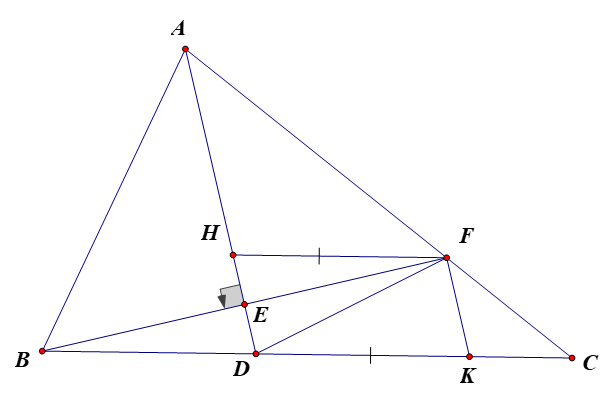
(c-g-c) suy ra: (1)
có là góc ngoài nên (2)
Từ (1) (2) có : hay: