30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 17)
-
6101 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết mạch điện xoay chiều chỉ chứa R
Cách giải:
Dòng điện xoay chiều trong đoạn mạch chỉ có điện trở thuần cùng tần số và cùng pha với điện áp giữa hai đầu đoạn mạch.
Chọn B.
Câu 2:
Mạch dao động điện từ dao động tự do với tần số góc riêng là . Biết điện tích cực đại trên tụ điện là , cường độ dòng điện cực đại qua cuộn dây được tính bằng biểu thức
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức liên hệ giữa I0 và q0 trong mạch dao động.
Cách giải:
Biểu thức liên hệ: I0 = ω.q0
Chọn D.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức định luật Ôm đối với toàn mạch: \[I = \frac{E}{{R + r}}\]
Cách giải:
Cường độ dòng điện trong mạch: \[I = \frac{E}{{R + r}}\]
Chọn A.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính tổng trở: \[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]
Cách giải:
Tổng trở của đoạn mạch gồm R nối tiếp cuộn cảm L là:
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {\omega L} \right)}^2}} }}\]
Chọn A.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng phương trình dòng điện xoay chiều: i = I0.cos(ωt+φ) = I\[\sqrt 2 \].cos(ωt+φ)
Cách giải:
Dòng điện xoay chiều có biểu thức \[i = 4\sqrt 2 \cos \left( {100\pi t + \pi /3} \right)\,A\].
Nên I = 4A
Chọn D.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lý thuyết về dao động tắt dần
Cách giải:
Trong dao động tắt dần biên độ và cơ năng của con lắc giảm dần theo thời gian nguyên nhân do quả cầu có sự ma sát với không khí nên một phần cơ năng chuyển hóa thành nhiệt năng.
Chọn D.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Sơ đồ khối của một máy thu sóng điện từ đơn giản gồm: anten (1), mạch chọn sóng (2), mạch tách sóng (3), mạch khuếch đại dao động điện từ âm tần (4) và loa (5).
Cách giải:
Mạch biến điệu nằm trong mạch phát sóng điện từ.
Chọn A.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng định nghĩa sóng dọc.
Cách giải:
Sóng dọc là sóng có phương dao động của các phần tử sóng trùng với phương truyền sóng.
Chọn B.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Ba đặc trưng sinh lí của âm là độ cao, độ to và âm sắc.
Cách giải:
Cường độ âm là đặc trưng vật lý của âm
Chọn A.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
- Biên độ dao động = ½ chiều dài quỹ đạo
Cách giải:
L = 10cm
Suy ra A = \[\frac{L}{2}\]= \[\frac{{10}}{2}\]= 5cm
Chọn A.Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính tốc độ góc của con lắc lò xo là ω = \[\sqrt {\frac{k}{m}} \]
Công thức tính tần số dao động của con lắc là: f = \[\frac{\omega }{{2\pi }}\]
Cách giải:
Tần số dao động của con lắc là: f = \[\frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \]
Chọn A.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính chu kì dao động của con lắc đơn: \[T = 2\pi \sqrt {\frac{l}{g}} \]
Cách giải:
A,B,D – sai
C- chu kì của con lắc đơn phụ thuộc vào chiều dài của con lắc
Chọn C.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Cách đo điện áp xoay chiều bằng đồng hồ vạn năng
Bước 1:Chèn dây dẫn màu đỏ vào cực dương của thiết bị và màu đen vào chân Com của vạn năng.
Bước 2:Di chuyển ním vặn đến thang đo điện áp AC và ở dải đo phù hợp. Bạn có thể để thang AC cao hơn điện áp cần đo 1 nấc.
Bước 3: Đặt 2 que đo vào 2 điểm cần đo (Đo song song). Không cần quan tâm đến cực tính của đồng hồ
Bước 4: Đọc kết quả hiển thị trên màn hình.
Cách giải:
A- DCV: đo điện áp 1 chiều
B- ACV: đo điện áp xoay chiều
C- DCA: đo dòng 1 chiều
D- ACA: đo dòng xoay chiều
Chọn B.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp: Sử dụng công thức tính vận tốc truyền sóng cơ: \[v = \lambda f\]
Cách giải:
Chọn B.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các công thức tính độ lớn của cảm ứng từ gây ra bởi dây dẫn có hình dạng đặc biệt
-1 điểm nằm cách dây dẫn thẳng dài 1 đoạn R là: \[B = {2.10^{ - 7}}\frac{I}{R}\]
-1 điểm nằm tại tâm vòng dây bán kính R là: \[B = 2\pi {.10^{ - 7}}\frac{I}{R}\]
-trong lòng ống dây có chiều lài l, gồm N vòng dây là: \[B = 2\pi {.10^{ - 7}}\frac{{NI}}{l}\]
Cách giải:
A- sai
B- độ lớn của cảm ứng từ gây ra tại 1 điểm nằm tại tâm vòng dây bán kính R
C- độ lớn của cảm ứng từ gây ra tại 1 điểm nằm cách dây dẫn thẳng dài 1 đoạn R
D- sai
Chọn C.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng khái niệm hai sóng kết hợp.
Cách giải:
Hai sóng kết hợp có cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian.
Chọn A.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng công thức: \[{s_0} = l.{\alpha _0}\]
Cách giải:
\[{s_0} = l.{\alpha _0}\]= 2.0,1 = 0,2m = 20cm
Chọn C.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính độ lệch pha giữ u và i trong mạch RLC mắc nối tiếp là: tanφ = \[\frac{{{Z_L} - {Z_c}}}{R}\]
Cách giải: độ lệch pha giữ u và i trong mạch điện xoay chiều gồm điện trở và tụ điện mắc nối tiếp là
tanφ =
⇒ φ = \[\frac{{ - \pi }}{4}\]
⇒ u trễ pha hơn i là \[\frac{\pi }{4}\]
Chọn B.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức thấu kính: \[\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\]
Cách giải:
Công thức xác định vị trí ảnh:
\[d' = \frac{{d.f}}{{d - f}} = \frac{{30.( - 20)}}{{30 - ( - 20)}} = 12\]cm
Chọn C.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Phương trình sóng tại 1 điểm trên phương truyền sóng: \[u = A\cos \left( {\omega t - \frac{{2\pi x}}{\lambda }} \right)(mm)\]
Cách giải: \[u = 4\cos \left( {50\pi t - 0,125{\rm{x}}} \right)(mm)\]
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính gia tốc cực đại: amax = ω2A
Cách giải: \[x = 3\cos 2\pi t\,\,(cm)\]
⇒ A= 3cm, ω = 2π(rad/s)
⇒ amax = ω2A = (2π)2.3 = 120 cm/s2 = 1,2m/s2
Chọn A.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính cường độ điện trường: E = \[\frac{F}{q}\]
Cách giải:
Cường độ điện trường tại M có độ lớn là: E = \[\frac{F}{q} = \frac{{{{6.10}^{ - 3}}}}{{{{2.10}^{ - 6}}}} = 3000\]V/m
Chọn B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng định nghĩa sóng dọc và sóng ngang:
- Sóng dọc là sóng có phương dao động của các phần tử sóng trùng với phương truyền sóng.
-Sóng ngang là sóng có phương dao động của các phần tử sóng vuông góc với phương truyền sóng.
Cách giải:
Chọn C.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính vận tốc truyền sóng điện từ trong chân không:
Cách giải:
Chọn C.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
Phương trình sóng tại 1 điểm M trên phương truyền sóng là \({u_M} = ac{\rm{os}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right)\,\,\)
Cách giải:
Phương trình sóng tại 1 điểm M cách O khoảng \[\frac{\lambda }{3}\] là:
\({u_M} = ac{\rm{os}}\left( {\frac{{2\pi }}{T}t - \frac{{2\pi x}}{\lambda }} \right)\,\,\)
⇒ \({u_M} = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{6} - \frac{{2\pi }}{\lambda }.\;\frac{\lambda }{3}} \right)\,\,\)= 2
⇒ \(ac{\rm{os}}\left( {\frac{{ - \pi }}{6}} \right)\,\,\)= 2
⇒ a.\[\frac{1}{2}\]= 2
⇒ a = 4cm
Chọn C.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng phương trình dao động của con lắc lò xo:
+ Sử dụng phương trình vận tốc của con lắc lò xo:
Cách giải:
⇒⇒
⇒= A
Chọn D .
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các công thức tính của con lắc lò xo treo thẳng đứng.
Năng lượng dao động của vật là: \[{\rm{W}} = \frac{1}{2}k.{A^2}\]
Cách giải:
Ta khi lò xo có chiều dài 28cm thì v = 0 và Fđh =2N ⇒ 2=k.0,02⇒k=100N/m
Tại VTCB: P=Fđh ⇒ m.g = k.Δl
⇒ Δl = \[\frac{{m.g}}{k} = \frac{{0,2.10}}{{100}} = 0,02\]m
⇒ biên độ dao động: A = Δl+ 0,02 = 0,04 m
⇒ Năng lượng dao động của vật là: \[{\rm{W}} = \frac{1}{2}k.{A^2} = \frac{1}{2}{.100.0,04^2} = 0,08\]J
Chọn B.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Công thức tính bước sóng:
+ Công thức xác định số điểm dao động với biên độ cực đại là:
Cách giải:
Bước sóng:
Số điểm dao đọng với biên độ cực đại là:
\[ \Rightarrow k = 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, \pm 6, \pm 7\]
\[ \Rightarrow \]có 15 giá trị thỏa mãn
Chọn C.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức của máy biến thế: \[\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\]
Cách giải:
Áp dugnj công thức: \[\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \Leftrightarrow \frac{{1000}}{{{U_2}}} = \frac{{2000}}{{100}}\]
\[ \Rightarrow \]U2 = 50 vòng
Chọn B.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Mạch chỉ có cuộn cảm thuần L: \[{u_L}\] nhanh pha hơn i một góc \[\frac{\pi }{2}\]
+ Hệ thức vuông pha: \[{\left( {\frac{i}{{{I_0}}}} \right)^2}{\left( { + \frac{{{u_L}}}{{U_{0L}^2}}} \right)^2} = 1\]
Cách giải:
Đoạn mạch chỉ chứa cuộn cảm thuần L: \[{u_L}\] nhanh pha hơn i một góc \[\frac{\pi }{2}\]
⇒ \[i = {I_0}\cos \left( {100\pi t + \frac{\pi }{3} - \frac{\pi }{2}} \right)\,\,V = {I_0}\cos \left( {100\pi t - \frac{\pi }{6}} \right)\]
ZL= L.ω = 100π.\[\frac{1}{\pi }\]= 100Ω
Hệ thức vuông pha của \[{u_L}\]và i: \[\begin{array}{l}{\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1\\ \Rightarrow {\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{I_0}{Z_L}}}} \right)^2} = 1\\ \Rightarrow I_0^2 = {i^2} + \frac{{{u^2}}}{{Z_L^2}} = {2^2} + \frac{{{{(100\sqrt 2 )}^2}}}{{{{100}^2}}} = 6\end{array}\]
⇒ I0 = \[\sqrt 6 \]
⇒\[i = \sqrt 6 \cos \left( {100\pi t - \frac{\pi }{6}} \right)\]
Chọn B.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
+ áp dụng công thức tính bước sóng cho từng trường hợp
Cách giải:
=60
⇒
⇒ C+=4C
⇒ C =2.10-12(F)
⇒
Chọn A.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức tính từ thông cực đại:
+ Biểu thức từ thông qua khung dây:
Cách giải:
Tại t=0 là lúc pháp tuyến của khung dây có chiều trùng với chiều của vecto cảm ứng từ
⇒ α = 0 ⇒ ⇒ φ=0
⇒
Chọn D.
Câu 33:
Một hộ gia đình sử dụng các thiết bị điện, với tổng công suất của các thiết bị điện sử dụng là 1200 W. Hỏi với công suất như trên thì trong một tháng (30 ngày) hộ gia đình này phải trả khoảng bao nhiêu tiền điện. Bởi rằng trung bình mỗi ngày hộ gia đình này sử dụng các thiết bị với tổng công suất như trên) liên tục trong 10 giờ và đơn giá mỗi kWh điện được tính lũy tiến như sau:
|
Số kWh tiêu thụ |
Từ 0 đến 50 |
Từ 51 đến 100 |
Từ 101 đến 200 |
Từ 201 đến 300 |
Từ 300 trở lên |
|
Đơn giá mỗi kWh |
1500 đồng |
1600 đồng |
1800 đồng |
2100 đồng |
2500 đồng |
 Xem đáp án
Xem đáp án
Phương pháp:
+ Tính tổng lượng điện tiêu thụ trong tháng
+ Tính giá tiền theo từng mức rồi cộng lại
Cách giải:
Tổng lượng điện tiêu thụ trong tháng: 1200.10.30=360000Wh=360kWh
Số tiền điện phải trả là:
Chọn D.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng giản đồ vecto
Cách giải:
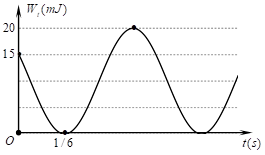
Vật dao động từ vị trí: Wt = ¾
⇒ ½ k.x2 = ¾ . ½ .k.A2
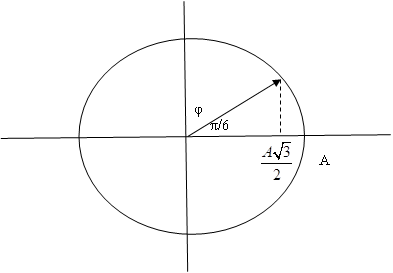
⇒ x =
Đến vị trí có Wt = 0 ⇒ x=0 trong thời gian Δt = 1/6 (s) ⇒ Δφ=
⇒ 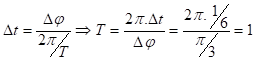
Từ đồ thị ta thấy tại t = 0 Wt đang giảm
⇒ phương trình có thể là
Chọn B.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính sai số tuyệt đối:
Cách giải:
+ Vận tốc trung bình: = 330m/s
+ Sai số tuyệt đối: m
⇒ tốc độ truyền âm trong không khí tại nơi làm thí nghiệm là: (330 ± 12) m/s
Chọn C.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Biểu thức liên hệ: I0 = ω.q0
+ Sử dụng phương trình dòng điện xoay chiều: i = I0.cos(ωt+φ) = I\[\sqrt 2 \].cos(ωt+φ)
Cách giải:
⇒ I0 = ω.q0= 6.10-4.2.104 =12A
Tại t = 0 thì q = Q0 I0 = ω.q0⇒φ=\[\frac{\pi }{2}\]
⇒ i = 12.cos(2.104t+\[\frac{\pi }{2}\])
Chọn D.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính tổng trở: \[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]
Cách giải:
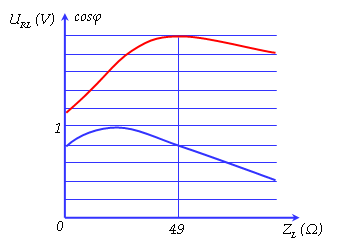
Dựa vào đồ thị ta thấy khi ZL = 49 thì URLmax khi đó cosφ = 0,8
URL = \[\frac{U}{Z}.{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\]
URLmax ⇒ \[Z_L^2 - {Z_L}.{Z_C} - {R^2} = 0\]⇒ ZC = 49 -\[\frac{{{R^2}}}{{49}}\]
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {49 - (49 - \frac{{{R^2}}}{{49}})} \right)}^2}} }}\]
=\[\frac{R}{{\sqrt {{R^2} + {{\left( {\frac{{{R^2}}}{{49}}} \right)}^2}} }}\]=0,8
⇒ R = 36,75Ω
Chọn D.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng giản đồ vecto
Cách giải:
⇒U0RL = V
⇒ uRL=\[200\sqrt 3 .c{\rm{os(100}}\pi {\rm{t + }}\frac{\pi }{6})\]
Chọn D.
Câu 39:
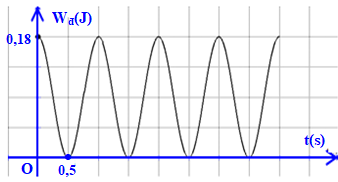
Một con lắc lò xo dao động điều hòa, động năng của con lắc biến thiên theo thời gian được biểu thị như hình vẽ, lò xo có độ cứng 100 N/m. Biết trong nửa chu kì đầu kể từ thời điểm t = 0 s con lắc có li độ âm. Con lắc dao động với phương trình là
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức tính động năng, thế năng, cơ năng của dao đọng điều hòa.
+ kĩ năng đọc đồ thị.
Cách giải:
Tại t=0 thì Wđ =0,18J=W
Tại t = 0,5 thì Wđ = 0 ⇒Wt = W = 0,18J
⇒\[\frac{1}{2}k{A^2} = 0,18J\]⇒ A = 0,06m = 6cm
Chọn C
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức hiệu đường truyền từ 1 điểm nằm trên
cực đại đến 2 nguồn: d2-d1=kλ
Cách giải:
Để trên MN có đúng 5 cực đại thì M và N nằm trên cực địa bậc 2
⇒ NB-NA=2λ
Chọn A.