30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 22)
-
5988 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Dao động tắt dần có biên độ và cơ năng giảm dần theo thời gian.
Cách giải:
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Chọn A.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Đọc phương trình dao động điều hòa: \[x = A\cos (\omega t + \varphi )\]
+ A: Biên độ dao động
+ ω: Tần số góc
+ (ωt + φ): Pha dao động tại thời điểm t
+ φ: Pha dao động tại thời điểm ban đầu.
Cách giải:
Phương trình dao động của vật: \[x = A\cos (\omega t + \varphi )\]
⇒ Tần số góc của dao động: ω
Chọn C.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính lực điện: \[\vec F = q\vec E\]
Cách giải:
Một điện tích điểm q đặt tại nơi có cường độ điện trường \(\overrightarrow E \) thì lực điện tác dụng lên điện tích đó là: \[\vec F = q\vec E\]
Chọn B.Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Quang phổ liên tục là một dải có màu từ đỏ đến tím nối liền nhau một cách liên tục.
+ Quang phổ liên tục do các chất rắn, chất lỏng hoặc chất khí có áp suất lớn phát ra khi bị nung nóng.
+ Quang phổ liên tục của các chất khác nhau ở cùng một nhiệt độ thì giống nhau và chỉ phụ thuộc vào nhiệt độ của chúng.
+ Ứng dụng: Đo nhiệt độ của các vật nóng sáng ở nhệt độ cao như các ngôi sao qua quang phổ của nó.
Cách giải:
A, C, D – sai vì quang phổ liên tục chỉ phụ thuộc vào nhiệt độ của vật.
B - đúng
Chọn B.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng kiến thức về các hiện tượng quang.
Cách giải:
Khi chiếu chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexein thì thấy dung dịch này phát ra ánh sáng màu lục đó là hiện tượng quang – phát quang.
Chọn A.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính suất điện động của bộ nguồn mắc song song: \[{\xi _b} = {\xi _1} = {\xi _2}\]
Cách giải:
Suất điện động của bộ nguồn: \[{\xi _b} = {\xi _1} = {\xi _2} = \xi \]
Chọn A.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Thuyết lượng tử ánh sáng:
+ Chùm ánh sáng là chùm các phôtôn (các lượng tử ánh sáng). Mỗi phôtôn có năng lượng xác định (năng lượng của 1 phôtôn:
+ Các phôtôn bay dọc theo tia sáng với tốc độ c = 3.108 m/s trong chân không.
+ Năng lượng của mỗi phôtôn rất nhỏ. Một chùm sáng dù yếu cũng chứa rất nhiều phôtôn do rất nhiều nguyên tử, phân tử phát ra. Vì vậy ta nhìn thấy chùm sáng liên tục.
+ Phôtôn chỉ tồn tại trong trạng thái chuyển động. Không có phôtôn đứng yên.
+ Các photon trong chùm ánh sáng đơn sắc thì có cùng năng lượng.
Cách giải:
A – sai vì mỗi photon mang một năng lượng xác định và phụ thuộc vào tần số ε = hf
B, C, D - đúng
Chọn A.Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về dòng điện trong kim loại.
Cách giải:
Hạt tải điện trong kim loại là electron tự do.
Chọn C.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện có cộng hưởng điện: \[{Z_L} = {Z_C}\] hay
Độ lệch pha giữa u và i:
Cường độ dòng điện hiệu dụng: \[I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]
Công suất tiêu thụ: \[P = \frac{{{U^2}R}}{{{Z^2}}} = \frac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\]
Tổng trở: \[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
Cách giải:
Ta có: \[f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow {Z_L} = {Z_C}\] mạch xảy ra cộng hưởng. Khi đó:
cùng pha.
+ C – sai vì: Tổng trở của mạch cực tiểu \[{Z_{\min }} = R\]
Chọn C.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về sự truyền ánh sáng.
+ Ánh sáng đơn sắc không bị tán sắc mà bị lệch khỏi phương truyền ban đầu khi đi qua lăng kính.
+ Chiếu ánh sáng từ môi trường này sang môi trường khác thì tần số không thay đổi.
Cách giải:
Khi chiếu ánh sáng đơn sắc tới lăng kính thì khi đi qua lăng kính, ánh sáng bị lệch khỏi phương truyền ban đầu và không bị tán sắc.
Chọn A.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
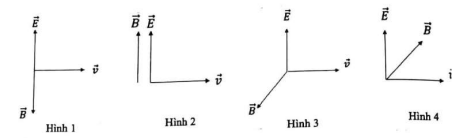
Sử dụng lí thuyết về sóng điện từ: \[\overrightarrow E ,\overrightarrow v .\overrightarrow B \] tạo với nhau một tam diện thuận.
Cách giải:
Ta có: \[\overrightarrow E ,\overrightarrow v .\overrightarrow B \] tạo với nhau một tam diện thuận ⇒ Hình vẽ diễn tả đúng là: Hình 3.
Chọn C.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Khoảng cách giữa 2 vân tối hoặc hai vân sáng liên tiếp bằng khoảng vân i.
+ Sử dụng biểu thức tính khoảng vân: \[i = \frac{{\lambda D}}{a}\]
Cách giải:
Khoảng cách giữa 2 vân tối liên tiếp: \[i = \frac{{\lambda D}}{a}\]
Chọn B.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về các loại phóng xạ.
Cách giải:
Tia α là chùm hạt nhân \[_2^4{\rm{He}}\]
Chọn D.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
Tia X được dùng để:
+ Chụp X – quang trong y học để chuẩn đoán và chữa trị một số bệnh.
+ Tìm khuyết tật trong vật đúc bằng kim loại và trong tinh thể.
+ Kiểm tra hành lý của hành khách đi máy bay.
+ Sử dụng trong phòng thí nghiệm để nghiên cứu thành phần và cấu trúc của các vật rắn.
Cách giải:
Ngoài ứng dụng trong y – tế, tia X còn có ứng dụng kiểm tra hành lí của hành khách đi máy bay.
Chọn A.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính hệ số công suất:
Cách giải:
Hệ số công suất của đoạn mạch là:
Chọn B.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính bước sóng:
Cách giải:
Bước sóng:
Chọn A.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Hạt nhân có kí hiệu: \[_Z^AX,\] trong đó:
+ Z = Số proton = Số electron
+ N = A – Z = Số notron
Cách giải:
Hạt nhân: \[_Z^AX\]có: Z số proton và (A – Z) số notron.
Chọn C.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức của cường độ dòng điện xoay chiều: \[i = {I_0}\cos (\omega t + \varphi )\]
Trong đó: I0 là cường độ dòng điện cực đại; ω là tần số góc; φ là pha ban đầu.
Cách giải:
Biểu thức cường độ dòng điện xoay chiều: \[i = {I_0}\cos (\omega t + \varphi )\]
Đại lượng I0 là cường độ dòng điện cực đại.
Chọn B.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sóng dọc là sóng có các phần tử của môi trường có phương dao động trùng với phương truyền sóng.
+ Sóng ngang là sóng có các phần tử của môi trường có phương dao động vuông góc với phương truyền sóng.
Cách giải:
Sóng dọc là sóng có các phần tử của môi trường có phương dao động trùng với phương truyền sóng.
Chọn A.Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Khoảng cách giữa hai bụng sóng hoặc hai nút sóng liên tiếp là \[\frac{\lambda }{2}\]
Khoảng cách giữa 1 nút sóng và 1 bụng sóng liên tiếp là \[\frac{\lambda }{4}\]
Cách giải:
Khoảng cách giữa 2 nút sóng liên tiếp bằng \[\frac{\lambda }{2}\]
Chọn D.Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về máy biến áp.
Cách giải:
A – sai vì máy biến áp là thiết bị biến đổi điện áp dòng điện xoay chiều.
B – sai vì lõi thép của máy biến áp được làm bằng các lá sắt hoặc thép pha silic.
C – sai vì hai cuộn dây của máy biến áp có số vòng khác nhau.
D – đúng vì máy biến áp hoạt động dựa vào hiện tượng cảm ứng điện từ.
Chọn D.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính tần số dao động riêng: \[f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \]
Cách giải:
Tần số dao động riêng của con lắc lò xo: \[f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \]
Chọn D.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng tiên đề về sự bức xạ và hấp thụ năng lượng của nguyên tử:
Cách giải:
Năng lượng của photon mà nó hấp thụ là:
Chọn D.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính năng lượng liên kết: \[{W_{lk}} = \left( {Z.{m_n} + (A - A).{m_n} - {m_X}} \right){c^2}\]
+ Sử dụng biểu thức tính năng lượng liên kết riêng:
Cách giải:
+ Năng lượng liên kết của hạt nhân \[{}_{^1}^2D:\]
\[{W_{lk}} = (1.1,0073u + 1.1,0087u - 2,0136u){c^2} = {2,4.10^{ - 3}}u{c^2} = 2,2356MeV\]
+ Năng lượng liên kết riêng của hạt nhân \[_1^2D\]là:
Chọn A.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
Tần số dao động của con lắc đơn: \[f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \]
Cách giải:
Ta có Tần số dao động của con lắc: \[f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \]\[ \Rightarrow l = \frac{g}{{4{\pi ^2}{f^2}}} = \frac{{{\pi ^2}}}{{4{\pi ^2}{{.0,5}^2}}} = 1m = 100cm\]
Chọn B.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính suất điện động tự cảm trong ống dây:
Cách giải:
Độ lớn suất điện động tự cảm trong ống dây: \[{e_{tc}} = \left| { - L\frac{{\Delta i}}{{\Delta t}}} \right| = \left| { - 0,5 \cdot \frac{{0,06 - 0,02}}{{0,01}}} \right| = 2V\]
Chọn B.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính dung kháng: \[{Z_C} = \frac{1}{{\omega C}}\]
Cách giải:
Dung kháng \[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi \frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \]
Chọn B.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính tần số góc mạch LC:
Cách giải:
Tần số góc dao động mạch LC là:
Chọn B.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính năng lượng photon:
Cách giải:
Mỗi photon của chùm sáng mang năng lượng là:
Chọn A.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng biểu thức tính chu kì dao động con lắc lò xo: \[T = 2\pi \sqrt {\frac{m}{k}} \]
Cách giải:
Ta có:
Chọn C.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính bước sóng:
+ Viết phương trình sóng tại M:
Cách giải:
+ Bước sóng:
+ Phương trình sóng tại M: \[{u_M} = 4\cos \left( {10\pi t - \frac{{2\pi .0,5}}{2}} \right) = 4\cos \left( {10\pi t - \frac{\pi }{2}} \right)cm\]
Chọn A.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức sóng dừng trên dây 2 đầu cố định: \[l = k\frac{\lambda }{2}\]
Trong đó: k = số bụng sóng.
Cách giải:
Điều kiện có sóng dừng trên dây hai đầu cố định: \[l = k\frac{\lambda }{2}\]
Với: \[\left\{ {\begin{array}{*{20}{l}}{l = 60cm = 0,6m}\\{v = 4m{\rm{/}}s}\\{k = 3}\end{array}} \right.\] \[ \Rightarrow l = k\frac{v}{{2f}} \Leftrightarrow 0,6 = 3\frac{4}{{2f}} \Rightarrow f = 10Hz\]
Chọn A.
Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Khoảng thời gian ngắn nhất từ khi tụ điện đang có điện tích điện cực đại đến khi điện tích của tụ điện bằng không là \[\frac{T}{4}\]
+ Sử dụng biểu thức tính bước sóng: λ = v.T
Cách giải:
Khoảng thời gian ngắn nhất từ khi tụ điện đang có điện tích cực đại đến khi điện tích của tụ bằng không:
\[\frac{T}{4} = {75.10^{ - 9}} \Rightarrow T = {3.10^{ - 7}}s\]
Bước sóng:
Chọn C.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng hệ thức liên hệ: \[{v^2} - v_0^2 = 2as\]
+ Sử dụng biểu thức tính tần số góc:
+ Sử dụng định luật bảo toàn động lượng
+ Sử dụng hệ thức độc lập: \[{A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\]
Cách giải:
Vận tốc của m’ ngay trước khi va chạm:
Tần số góc của hệ:
Vị trí cân bằng mới thấp hơn vị trí cân bằng cũ 1 đoạn: \[{x_0} = \frac{{m'g}}{k} = \frac{{{{50.10}^{ - 3}}.10}}{{100}} = {5.10^{ - 3}}m\]
Vận tốc của hệ sau va chạm: \[V = \frac{{m'v}}{{m' + m}} = \frac{{0,05.4,85}}{{0,05 + 0,625}} = 0,359m{\rm{/}}s\]
Biên độ sau va chạm: \[A = \sqrt {{{\left( {{A_0} - {x_0}} \right)}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \]
Chọn C.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Vận dụng tính chất về pha dao động
+ Sử dụng biểu thức tính li độ dao động tổng hợp: \[x = {x_1} + {x_2}\]
Cách giải:
Ta có: hai dao động ngược pha nên: \[{x_1} = {A_1}\cos (\omega t + \varphi )\] và
Khi:
Khi đó, li độ tổng hợp: \[x = {x_1} + {x_2} = 0,5\left( {{A_1} - {A_2}} \right)\]
Chọn C.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
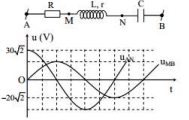
+ Đọc đồ thị u-t
+ Sử dụng biểu thức tính công suất:
+ Sử dụng biểu thức tính hệ số công suất:
Cách giải:
Từ đồ thị, ta có: \[\left\{ {\begin{array}{*{20}{l}}{{u_{AN}} = 30\sqrt 2 \cos (\omega t)}\\{{u_{MB}} = 20\sqrt 2 \cos \left( {\omega t - \frac{\pi }{2}} \right)}\end{array}} \right.\] \[ \Rightarrow {u_{AN}} \bot {u_{MB}} \Rightarrow {\cos ^2}{\varphi _{AN}} + {\cos ^2}{\varphi _{MB}} = 1\]
Lại có: \[{P_{AM}} = {P_{MN}} \Leftrightarrow UI \cdot \frac{R}{Z} = UI\frac{r}{Z} \Rightarrow R = r \Rightarrow {U_R} = {U_r}\]
Thay vào (1) ta được: \[{\left( {\frac{{2{U_R}}}{{30}}} \right)^2} + {\left( {\frac{{{U_R}}}{{20}}} \right)^2} = 1 \Rightarrow {U_R} = {U_r} = 12V\]
Lại có:
Hệ số công suất của đoạn mạch AB:
Chọn A.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về hai vân sáng trùng nhau trong giao thoa ánh sáng
+ Hai vân trùng nhau: \[{x_1} = {x_2}\]
+ Vị trí vân sáng: \[{x_S} = ki = k\frac{{\lambda D}}{a}\]
Cách giải:
+ Số vân sáng trùng nhau trên đoạn AB: \[{N_ \equiv } = 19 - 6 - 10 = 3\]
+ Số vân sáng của bức xạ 1: \[{N_1} = 6 + 3 = 9\]
+ Số vân sáng của bức xạ 2: \[{N_2} = 10 + 3 = 13\]
Chiều dài đoạn AB: \[L = 8{i_1} = 12{i_2} \Leftrightarrow 8\frac{{{\lambda _1}D}}{a} = 12\frac{{{\lambda _2}D}}{a} \Rightarrow {\lambda _2} = \frac{{8{\lambda _1}}}{{12}} = \frac{{8.0,69}}{{12}} = 0,46\mu m\]
Chọn A.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biều thức: \[U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \]
+ Sử dụng biểu thức:
+ Sử dụng biểu thức tính công suất:
Cách giải:
Ta có: \[\left\{ {\begin{array}{*{20}{l}}{U = 50\sqrt 2 V}\\{{U_L} = 100V}\\{{U_C} = 50V}\end{array}} \right.\]
Lại có:
Hệ số công suất của mạch:
Công suất tiêu thụ của mạch:
Mặt khác: \[P = {I^2}R \Rightarrow R = \frac{P}{{{I^2}}} = \frac{{100}}{{{2^2}}} = 25\Omega \]
Chọn B.
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng biểu thức tính công suất hao phí: \[\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R\]
Cách giải:
+ Ban đầu: \[{U_0} = U\] thì công suất hao phí: \[\Delta P = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}R\]
+ Khi \[{U_1} = U + 100(kV)\] thì công suất hao phí: \[\Delta {P_1} = \frac{{\Delta P}}{4} = \frac{{{P^2}}}{{{{(U + 100)}^2}{{\cos }^2}\varphi }}R\]
\[ \Rightarrow 4{U^2} = {(U + 100)^2} \Rightarrow U = 100(kV)\]
+ Khi \[{U_2} = U + 300(kV)\] thì công suất hao phí: \[\Delta {P_2} = \frac{{{P^2}}}{{{{(U + 300)}^2}{{\cos }^2}\varphi }}R = \frac{{{P^2}}}{{{{(4U)}^2}{{\cos }^2}\varphi }}R = \frac{{\Delta P}}{{16}}\]
⇒ Công suất hao phí giảm 16 lần.
Chọn D.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính số điểm dao động cực đại trên đường thẳng nối 2 nguồn cùng pha: \[ - \frac{{{S_1}{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda }\]
+ Vận dụng biểu thức xác định vị trí cực đại giao thoa: \[{d_2} - {d_1} = k\lambda \]
+ Sử dụng hệ thức trong tam giác.
Cách giải:
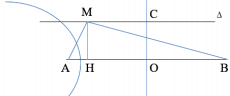
Ta có:
Gọi M là cực đại trên Δ xa C nhất.
Số cực đại trên AB bằng số giá trị k nguyên thỏa mãn:
⇒ M là cực đại bậc 3
Ta có: \[MB - MA = 3\lambda \]
Gọi H – là hình chiếu của M trên AB
+ Trường hợp H nằm trong AB:
+ Trường hợp H nằm ngoài AB:
Chọn D.