30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 24)
-
6102 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Phương trình sóng tại điểm M cách nguồn 1 đoạn d là:
Thay t vào phương trình của uM
Cách giải:
Phương trình sóng: \(u = 5\cos \left( {10\pi t - \frac{{\pi x}}{2}} \right)(mm)\)
Điểm M cách O 1m nên thời gian sóng truyền từ O đến M là: \(t = \frac{s}{v} = \frac{1}{{0,2}} = 5s\)
⇒ Tại thời điểm \[t = 2s\] sóng chưa truyền tới M nên \({u_M} = 0\)
Chọn D.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức của từ thông và suất điện động cảm ứng:
Cách giải:
Ta có:
Chọn A.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức định luật Ôm: \(I = \frac{U}{Z}\)
Công thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Cách giải:
Tổng trở của đoạn mạch: Cường độ dòng điện hiệu dụng qua cuộn dây: \(I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + {\omega ^2}{L^2}} }}\)
Chọn C.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Biên độ của dao động tổng hợp: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos (\Delta \varphi )\)
Hai dao động cùng pha. \[A = {A_1} + {A_2}\]
Hai dao động ngược pha. \(A = \left| {{A_1} - {A_2}} \right|\)
Cách giải:
Ta có:
⇒ Biên độ dao động tổng hợp của 2 dao động thỏa mãn: \(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)
Chọn C.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Đoạn mạch chỉ có tụ điện:
Cách giải:
+ Tổng trở:
+ Cường độ dòng điện cực đại: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{120}}{{100}} = 1,2A\)
+ i sớm pha hơn
⇒Phương trình cường độ dòng điện là: \(i = 1,2\cos \left( {100\pi t + \frac{\pi }{3}} \right)(A)\).
Chọn A.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính chu kì của con lắc đơn:
Công thức tính gia tốc trọng trường. \(g = \frac{{GM}}{{{{(R + h)}^2}}}\)
Cách giải:
Ta có:
Gia tốc trọng trường: \({g_h} = \frac{{GM}}{{{{(R + h)}^2}}}\)
Khi đưa con lắc đơn lên cao theo phương thẳng đứng (chiều dài dây treo không đổi) ⇒ h tăng ⇒ gh giảm ⇒ chu kỳ con lắc tăng.
Chọn D.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức liên hệ giữa tần số và bước sóng: \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Bước sóng theo thứ tự tăng dần: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại
Cách giải:
Bảng thang sóng điện từ:
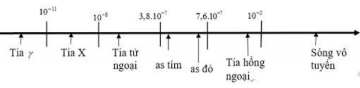
Có \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Tần số các sóng điện từ theo thứ tự giảm dần là: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại.
Chọn A.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Đặc điểm của quang phổ liên tục:
+ Không phụ thuộc vào cấu tạo vật chất
+ Phụ thuộc vào nhiệt độ của vật phát sáng.
Cách giải:
Quang phổ liên tục phát ra bởi hai vật khác nhau giống nhau nếu chúng có cùng nhiệt độ.
Chọn D.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Đặc điểm của sóng điện từ
+ Sóng điện từ là sóng ngang
+ Trong quá trình truyền sóng luôn có phương vuông góc với nhau và vuông góc với phương truyền sóng nhưng biến thiên cùng pha.
Cách giải:
Do biến thiên cùng pha nên: \(E = {E_0}\cos 2\pi ft \Rightarrow B = {B_0}\cos 2\pi ft\)
Chọn C.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức của máy biến áp lí tưởng \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\)
1 1 U N
2 2
Cách giải:
Gọi vòng dây cuộn sơ cấp, thứ cấp là \({N_1},{N_2}.\) Gọi\({\rm{ }}{U_1},{U_2}\) tương ứng là điện áp hiệu dụng giữa hai đầu cuộn sơ cấp, thứ cấp.
Biểu thức liên hệ giữa các đại lượng trên là: \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\).
Chọn C.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Tần số góc, tần số, chu kì dao động của con lắc lò
Cách giải:
Tần số dao động của vật được tính bằng công thức: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} .\)
Chọn B.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp: \(i = \frac{{\lambda D}}{a}\)
Cách giải:
Công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)
Chọn A.
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Cảm ứng từ của dòng điện chạy trong dây dẫn thẳng dài:
Cách giải:
Cảm ứng từ do dòng điện chạy trong dây dẫn thẳng dài gây ra tại
⇒ \({B_M} - \frac{1}{r} \Rightarrow \) tăng khi r giảm ⇒ M dịch chuyển vuông góc với dây là lại gần dây.
Chọn C.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
Trong giao thoa sóng hai nguồn cùng pha:
+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda ;k \in Z\)
+ Điều kiện có cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda ;k \in Z\)
Cách giải:
Những điểm có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha thỏa mãn:
\({d_2} - {d_1} = k\lambda {\rm{ v?i }}k = 0; \pm 1; \pm 2; \ldots \)
Chọn A.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Tia tử ngoại và tia X đều sóng điện từ, có tác dụng lên kính ảnh, kích thích 1 số chất phát quang.
Cách giải:
Tia tử ngoại và tia X đều là sóng điện từ nên không bị lệch khi đi qua 1 điện trường mạnh
Chọn C.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Máy phát điện là các thiết bị dùng để biến đổi cơ năng thành điện năng.
Nguyên tắc hoạt động của các loại máy phát điện xoay chiều dựa trên hiện tượng cảm ứng điện từ: khi từ thông qua qua một vòng dây biến thiên điều hòa, trong vòng dây xuất hiện một suất điện động cảm ứng xoay chiều.
Cách giải:
Nguyên tắc hoạt động của máy phát điện xoay chiều một pha dựa trên hiện tượng cảm ứng điện từ.
Chọn C.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Phương trình dao động điều hòa của chất điểm \(x = A\cos (\omega t + \varphi )\)
Trong đó: A là biên độ; ω là tần số góc; \(\varphi \) là pha ban đầu.
Cách giải:
Phương trình dao động: \(x = 10\cos (15t + \pi )\)
⇒ Tần số góc dao động của chất điểm
Chọn B.
Câu 18:
Đặt điện áp \(u = {U_0}\cos (\omega t + \varphi )\) vào hai đầu đoạn mạch RLC nối tiếp có L thay đổi. Khi công suất của mạch cực đại thì L được xác định bằng biểu thức nào ?
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện có cộng hưởng điện: \[{Z_L} = {Z_C}\]
Công thức tính công suất: \(P = \frac{{{U^2}R}}{{{Z^2}}}\)
Cách giải:
Công suất của mạch được xác định bởi công thức: \(P = \frac{{{U^2}R}}{{{Z^2}}} = \frac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Mạch có L thay đổi để \({P_{\max }} \Leftrightarrow {\left[ {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \right]_{\min }}\)
Khi mạch xảy ra hiện tượng cộng hưởng khi đó công suất của mạch đạt giá trị cực đại
\( \Leftrightarrow {Z_L} = {Z_C} \Leftrightarrow \omega L = \frac{1}{{\omega C}} \Rightarrow L = \frac{1}{{{\omega ^2}C}}\)
Chọn D.
Câu 19:
Một con lắc lò xo nằm ngang có tần số góc dao động riêng \({\omega _0} = 10{\rm{rad}}/{\rm{s}}\). Tác dụng vào vật nặng theo phương của trục lò xo một ngoại lực biến thiên theo biểu thức \({F_n} = {F_0}\cos 20t(N)\)
Sau một thời gian vật dao động điều hòa với biên độ 5cm. Tốc độ cực đại của vật trong quá trình dao động bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp:
Tốc độ cực đại: \({v_{\max }} = \omega A\)
Tần số góc của dao động cưỡng bức bằng tần số của ngoại lực cưỡng bức
Cách giải:
Ngoại lực tác dụng: \({F_n} = {F_0}\cos 20t(N)\)
⇒Tần số góc của dao động cưỡng bức:
Biên độ dao động: \(A = 5\;{\rm{cm}}\)
⇒ Tốc độ cực đại: \({v_{\max }} = \omega A = 20.5 = 100\;{\rm{cm}}/{\rm{s}}\)
Chọn B.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức của q và i:
Cách giải:
Ta có:
⇒ i, q biến thiên điều hòa theo thời gian với cùng tần số, lệch pha nhau 1 góc \(\frac{\pi }{2}\)
Chọn B.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức liên hệ giữa công thoát và giới hạn quang điện: \({\lambda _0} = \frac{{hc}}{{{A_0}}}\)
Cách giải:
Giới hạn quang điện của kim loại này bằng: \({\lambda _0} = \frac{{hc}}{{{A_0}}} = \frac{{6,625 \cdot {{10}^{ - 34}} \cdot 3 \cdot {{10}^8}}}{{4 \cdot 1,6 \cdot {{10}^{ - 19}}}} = {3,1.10^{ - 7}}\;{\rm{m}} = 0,71\mu {\rm{m}}\)
Chọn A.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Quang điện trở được chế tạo dựa trên hiệu ứng quang điện trong. Đó là một tấm bán dẫn có giá trị điện trở thay đổi khi cường độ chùm sáng chiếu vào nó thay đổi.
Cách giải:
Nguyên tắc hoạt động của quang điện trở dựa trên hiện tượng quang điện trong
Chọn B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Các đặc trưng sinh lí của âm bao gồm độ cao, độ to, âm sắc gắn liền với 3 đặc trưng vật lí là tần số, mức cường độ âm và đồ thị dao động âm.
Cách giải:
Độ cao là một đặc trưng sinh lí của âm gắn liền với tần số của âm, âm càng cao khi tần số càng lớn.
⇒ Hai âm có cùng độ cao thì chúng sẽ có cùng tần số âm.
Chọn B.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính hiệu suất của nguồn điện : \(\left\{ {\begin{array}{*{20}{l}}{H = \frac{{{U_N}}}{E}.100\% }\\{H = \frac{{{A_{ich}}}}{{{A_{{\rm{nguon }}}}}}.100\% }\\{H = \frac{{{R_N}}}{{{R_N} + r}}.100\% }\end{array}} \right.\)
Trong đó E, r là suất điện động và điện trở trong của nguồn; RN là điện trở của mạch ngoài; UN là hiệu điện thế giữa 2 cực của nguồn.
Cách giải:
Ta có:
Hiệu suất của nguồn không được tính bởi công thức: \(H = \frac{r}{{{R_N} + r}}(100\% ).\)
Chọn D.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Các bộ phận của máy phát thanh: Micro, mạch phát sóng điện từ cao tần, mạch biến điệu, mạch khuếch đại, ăng ten phát.
+ Các bộ phận của máy thu thanh gồm: ăng ten thu, mạch khuếch đại dao động điện từ cao tần, mạch tách sóng, mạch khuyếch đại dao động điện từ âm tần, mạch tách sóng và loa.
Cách giải:
Trong sơ đồ khối của một máy phát thanh vô tuyến đơn giản và một máy thu thanh đơn giản đều có bộ phận ăng ten.
Chọn B.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2} \cdot \sin r\)
Điều kiện xảy ra hiện tượng phản xạ toàn phần: \(\left\{ {\begin{array}{*{20}{l}}{{n_1} > {n_2}}\\{\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}}\end{array}} \right.\)
Chiết suất của môi trường đối với ánh sáng đơn sắc: \[{n_d} < {n_t}\]
Cách giải:
Góc giới hạn phản xạ toàn phần được xác định bởi công thức: \({{\mathop{\rm sini}\nolimits} _{gh}} = \frac{1}{n}\)
Do \({n_d} < {n_t} \Rightarrow \sin {i_{ghdo}} > \sin {i_{ghtim}} \Rightarrow {i_{ghdo}} > {i_{ghtim}}\)
Tia ló đơn sắc màu lục đi là là mặt nước \( \Rightarrow i = {i_{ghuc}}\)
⇒ Chỉ có tia đỏ và vàng có góc giới hạn lớn hơn tia mà lục và ló ra khỏi nước,
Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Dòng điện xoay chiều ba pha được dùng với các thiết bị có công suất lớn: Máy sát gạo…
+ Dòng điện 1 pha sử dụng trong sinh hoạt gia đình, công suất thiết bị nhỏ, các thiết bị không bị hao phí về điện năng nhiều. Ví dụ: ti vi, tủ lạnh, máy giặt.
Cách giải:
Thiết bị dùng dòng điện xoay chiều 3 pha là máy sát gạo.
Chọn C.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức thấu kính: \(\frac{1}{d} + \frac{1}{{{d^\prime }}} = \frac{1}{f}\)
Cách giải:
Ảnh cùng chiều với vật ⇒ ảnh đó là ảnh ảo
Tiêu cự của thấu kính hội tụ \(f = 20\;{\rm{cm}}\)
Áp dụng công thức thấu kính ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}} \Leftrightarrow \frac{1}{{20}} = \frac{1}{d} + \frac{1}{{ - 30}} \Rightarrow d = 12\;{\rm{cm}}\)
Chọn D.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Độ lớn lực đàn hồi: \({F_{dh}} = k \cdot \left( {l - {l_0}} \right) = k \cdot \Delta l\)
Độ biến dạng tại VTCB: \(\Delta l = \frac{{mg}}{k}\)
Tần số góc:
Cách giải:
Phương trình dao động:
Độ cứng của lò xo: \(k = m \cdot {\omega ^2} = {0,1.10^2} = 10\;{\rm{N}}/{\rm{m}}\)
Độ giãn của lò xo tại VTCB: \(\Delta l = \frac{g}{{{\omega ^2}}} = \frac{{10}}{{{{10}^2}}} = 0,1\;{\rm{m}} = 10\;{\rm{cm}}\)
Tại t = 0 vật có \(x = 2\;{\rm{cm}}\) chuyển động theo chiều dương. Khi đi được quãng đường \(S = 10\;{\rm{cm}}\) thì vật đến đúng ở vị trí biên âm. Độ lớn lực đàn hồi tác dụng vào vật tại thời điểm đó là:
\({F_{dh}} = k \cdot (\Delta l + A) = 10.(0,1 + 0,04) = 1,4N\)
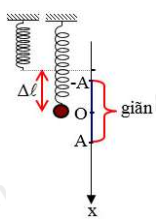
Chọn A.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các công thức:
Cách giải:
Từ các công thức:
Mà: \(\left\{ {\begin{array}{*{20}{l}}{{d_1} = 2d;{H_1} = 91\% }\\{{d_2} = 3d;{H_2}}\end{array}} \right.\)
Từ công thức hiệu suất: \(H = \frac{{P - \Delta P}}{P}.100\% \)
Từ (1) và (2)
\( \Rightarrow {H_2} = 96\% \)
Chọn B.
Câu 31:
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số: Tính tốc độ trung bình của vật từ lúc bắt đầu chuyển động đến khi qua vị trí cân bằng lần đầu.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng phương pháp đại số kết hợp máy tính cầm tay.
Công thức tính vận tốc trung bình: \({v_{tb}} = \frac{s}{t}\)
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} = 5\cos \left( {10\pi t - \frac{\pi }{3}} \right)({\rm{cm}})}\\{{x_2} = 5\sin \left( {10\pi t + \frac{\pi }{2}} \right)({\rm{cm}})}\end{array}} \right.\)
Phương trình dao động tổng hợp:
Từ lúc vật bắt đầu chuyển động đến khi qua vị trí cân bằng lần đầu, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{t = \frac{T}{{12}} + \frac{T}{4} = \frac{1}{{15}}(s)}\\{S = A + \left( {A - \frac{{A\sqrt 3 }}{2}} \right) = 9,82(\;{\rm{cm}})}\end{array}} \right.\)
Tốc độ trung bình của vật: \({v_{tb}} = \frac{s}{t} = \frac{{9,82}}{{\frac{1}{{15}}}} = 1,473(s)\)
Chọn B.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức xác định mức cường độ âm: \(L = 10\log \frac{I}{{{I_0}}}\)
Công thức tính cường độ âm: \(I = \frac{P}{{4\pi {r^2}}}\)
Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
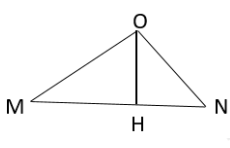
Công thức tính mức cường độ âm trên đoạn MN:
Với r là khoảng cách từ O đến 1 điểm trên MN.
⇒ \({L_{\max }} \Leftrightarrow {r_{\min }} = OH\) (với H là chân đường cao kẻ từ O xuống MN).
Áp dụng hệ thức lượng trong tam giác vuông OMN có:
\(OH = \frac{{OM \cdot ON}}{{MN}} = \frac{{80.60}}{{100}} = 48(\;{\rm{mm}})\)
Lại có:
\( \Rightarrow {L_H} = 50 + 20\log \frac{{OM}}{{OH}} = 50 + 20\log \frac{{80}}{{48}} \approx 54,4dB\)
Chọn A.
Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Bước sóng:
+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda ;k \in Z\)
Cách giải:
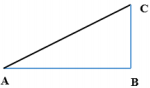
Phương trình dao động của hai nguồn:
\({u_A} = {u_B} = 5\cos \left( {20\pi t + \frac{{3\pi }}{4}} \right)({\rm{cm}};s)\)
Tốc độ truyền sóng: \(v = 0,2\;{\rm{m}}/{\rm{s}}\)
Bước sóng:
Bài cho \(AB = 30\;{\rm{cm}} \Rightarrow {\rm{AB}} = 15\lambda \)
Áp dụng định lí Pitago trong tam giác vuông ABC ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow A{B^2} = A{C^2} - B{C^2}\)
Mà:
Mặt khác: \({d_2} - {d_1} = k\lambda \left( 2 \right)\) (cực đại)
Từ (1) và (2) \( \Rightarrow {d_2} + {d_1} = \frac{{225}}{k}\lambda \)
Để cực đại cùng pha thì k và \(\frac{{225}}{k}\) hoặc cùng chẵn hoặc cùng lẻ, ở đây chỉ có k lẻ thỏa mãn.
Lại có: \({d_2} + {d_1} > 15\lambda \) (tổng hai cạnh bất kì của một tam giác luôn lớn hơn cạnh còn lại)
Lập bảng tìm các giá trị của k thỏa mãn:
|
k |
1 |
3 |
5 |
9 |
|
225 |
75 |
45 |
25 |
Để gần B nhất thì \({\left( {{d_2} + {d_1}} \right)_{\min }} \Leftrightarrow {\left( {\frac{{225}}{k}\lambda } \right)_{\min }} \Leftrightarrow {k_{\max }} = 9\)
Chọn D.
Câu 34:
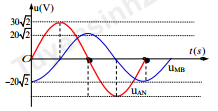
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị, phân tích mạch điện.
+ Sử dụng phương pháp vẽ giản đồ véc tơ.
+ Công suất tiêu thụ: \(P = \frac{{{U^2} \cdot R}}{{{Z^2}}}\)
+ Áp dụng định lí Pitago trong tam giác vuông.
Cách giải:
+ Mạch điện bao gồm điện trở, cuộn cảm có điện trở, tụ điện.
Nhìn vào đồ thị ta thấy, \[{U_{AN}},{U_{MB}}\] vuông pha vì: \[{U_{AN}}\] cực đại thì UMB cực tiểu và ngược lại.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{U_{AN}} = 30V}\\{{U_{MB}} = 20V}\\{{U_{AN}} \bot {U_{MB}}}\end{array}} \right.\)
+ Giản đồ véc tơ của mạch điện:
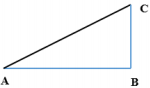
+ Công suất tiêu thụ trên đoạn AM bằng công suất tiêu thụ trên đoạn MN
\( \Rightarrow R = r \Rightarrow {U_R} = {U_r} \Rightarrow AM = MO\)
+ Từ giản đồ véc tơ ta thấy \(\cos NAM = \cos MBN\) (góc có cạnh tương ứng vuông góc, cạnh AO ⊥ AB, cạnh HB ⊥ AN)
\( \Rightarrow \frac{{AO}}{{AN}} = \frac{{OB}}{{MB}} \Rightarrow \frac{{2AM}}{{AN}} = \frac{{\sqrt {M{B^2} - O{M^2}} }}{{MB}} \Leftrightarrow \frac{{2{U_R}}}{{30}} = \frac{{\sqrt {{{20}^2} - U_r^2} }}{{20}} \Rightarrow {U_R} = 12\;{\rm{V}}\)
Áp dụng định lí Pitago trong tam giác vuông AOB có: \(A{B^2} = A{O^2} + O{B^2} \Leftrightarrow {U^2} = \sqrt {{{\left( {2{U_R}} \right)}^2} + {{\left( {{U_{MB}} - {U_r}} \right)}^2}} \)
Chọn C.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Xác định chiểu bằng quy tắc xòe bàn tay phải như sau, xòe bàn tay phải sao cho
- Lòng bàn tay hứng các đường cảm ứng từ (đường cảm ứng từ xuyên vào lòng bàn tay).
- Chiều từ cổ tay đến ngón giữa chỉ chiều truyền sóng.
- Ngón tay cái choãi ra 900 độ chỉ chiều điện trường.
+ Vecto cường độ điện trường và vecto cảm ứng từ biến thiên cùng pha, vuông phương.
Cách giải:
Do \(\vec E,\vec B\) cùng pha nên: \(\frac{e}{{{E_0}}} = \frac{B}{{{B_0}}} \Rightarrow B = \frac{{e \cdot {B_0}}}{{{E_0}}} = \frac{{20.0,3}}{{50}} = 0,12(T)\)
Sử dụng quy tắc bàn tay phải xác định được Bcó chiều hướng lên.
Chọn B.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức:
+ Hệ thức độc lập theo thời gian: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
+ Công thức liên hệ s, v, a của chuyển động thẳng biền đổi đều: \({v^2} - v_0^2 = 2as\)
Cách giải:
Ta có:
+ Sau khi kéo vật B xuống dưới 20cm và thả nhẹ ⇒ hệ dao động với biên độ: \(A = 20\;{\rm{cm}}\)
Vì \(\Delta l = 10cm < A \Rightarrow \) vật B đi lên đến vị trí lò xo không biến dạng, lực đàn hồi bị triệt tiêu.
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{s = 30\;{\rm{cm}}}\\{x = \frac{{ - A}}{2}}\end{array}} \right.\)
Sử dụng công thức độc lập ta có: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{{(A\omega )}^2}}} = 1 \Rightarrow \frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{v_{{{\max }^2}}}}} = 1\)
Mặt khác, vì vật B ném thẳng đứng lên trên nên chuyển động của B là chuyển động thẳng chậm dần đều. Áp dụng công thức liên hệ giữa s,v,a ta có:
⇒ Tổng quãng đường là: \(S = 30 + 15 = 45\;{\rm{cm}}\)
Chọn D.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Khi mạch xảy ra cộng hưởng điện: \[{Z_L} = {Z_C}\]
+ Công suất tiêu thụ của đoạn mạch: \(P = \frac{{{U^2}R}}{{{Z^2}}} = \frac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
+ Cường độ dòng điện hiệu dụng: \(I = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
+ L thay đổi để \({U_{L\max }}:\left\{ {\begin{array}{*{20}{l}}{{Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}}\\{{U_{L\max }} = \frac{{U\sqrt {{R^2} + Z_C^2} }}{R}}\end{array}} \right.\)
Cách giải:
+ Khi \({L_1} = \frac{1}{\pi } \Rightarrow {I_{\max }} \Rightarrow {Z_{L1}} = {Z_C} \Rightarrow P = \frac{{{U^2}}}{R} = 200\) (*)
+ Khi \({L_2} = \frac{2}{\pi } = 2{L_1} \Rightarrow {Z_{L2}} = 2{Z_{L1}}\)
\({U_{L\max }} \Rightarrow {Z_{L2}} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}} \Leftrightarrow 2.{Z_{L1}} = \frac{{{R^2} + Z_{L1}^2}}{{{Z_{L1}}}} \Rightarrow {Z_{L1}} = R = {Z_C}\)
\({U_{L\max }} = \frac{{U\sqrt {{R^2} + Z_C^2} }}{R} \Leftrightarrow 200 = \frac{{U\sqrt {{R^2} + {R^2}} }}{R} \Rightarrow U = 100\sqrt 2 V\)
Thay vào (*) ta có:
Lại có
Chọn D.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Vị trí vân sáng: \(x = k \cdot \frac{{\lambda D}}{a}\)
+ Vị trí vân tối: \(x = (k + 0,5) \cdot \frac{{\lambda D}}{a}\)
Cách giải: :
Vì dịch chuyển dần màn ra xa một đoạn nhỏ nhất bằng \(\frac{7}{{45}}m\) thì M chuyển thành vân tối, dịch ra xa thêm một đoạn nhỏ nhất bằng \(\frac{4}{9}m\) thì M lại là vân tối nên ta có:
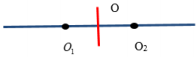
+ Tại O1 ta có: \({x_N} = {k^\prime } \cdot \frac{{\lambda (D - 0,5)}}{a} \Leftrightarrow 51,4 = {k^\prime } \cdot (1,4 - 0,5) \Rightarrow {k^\prime } = 7,7\)
+ Trong đoạn OO1 thì k có thể là \({k^\prime } = 5,5;6,5;7,5\)
+ Tại O2 ta có: \({x_N} = {k^\prime } \cdot \frac{{\lambda (D + 0,5)}}{a} \Rightarrow 51,4 = {k^\prime } \cdot (1,4 + 0,5) \Rightarrow {k^\prime } = 3,68\)
Trong đoạn OO2 thì k 'có thể là (4,5)
Trong khoảng thời gian \(\frac{T}{2}\) cho 4 vân sáng.⇒ Trong \[1s = 2T\] sẽ cho 16 vân sáng
Chọn B.
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện có sóng dừng trên sợi dây 1 đầu cố định, 1 đầu tự do: \(l = (k + 0,5) \cdot \frac{\lambda }{4} = (k + 0,5) \cdot \frac{v}{{4f}}\)
Tính chất của dãy tỉ số bằng nhau: \(\frac{a}{b} = \frac{c}{d} = \frac{{a - c}}{{b - d}}\)
Cách giải:
Điều kiện có sóng dừng trên dây 1 đầu là nút 1 đầu là bụng sóng: \(l = (k + 0,5) \cdot \frac{v}{{4f}}\)
Theo bài ra ta có: \(\left\{ {\begin{array}{*{20}{l}}{4,5 = (k + 0,5) \cdot \frac{v}{{2f}}\left( 1 \right)}\\{4,5 = (k + 18 + 0,5) \cdot \frac{v}{{(2f + 3)}}\left( 2 \right)}\end{array}} \right.\)
\( \Rightarrow \frac{{k + 0,5}}{f} = \frac{{k + 18,5}}{{f + 3}} = \frac{{18}}{3} = 6 \Rightarrow k + 0,5 = 6f\)
Thay vào (1) ta được: \(4,5 = 6f \cdot \frac{v}{{2f}} = 1,5(\;{\rm{m}}/{\rm{s}})\)
Chọn D.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính cường độ điện trường: \(E = k \cdot \frac{{|q|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường:
Cách giải:
Ta có nên N nằm trên đường thẳng AB và nằm ngoài AB.
Cường độ điện trường tổng hợp tại
Ta có:
![Hai điện tích \[{q_1} = {q_2} = 5nC\], đặt tại hai điểm A và B cách nhau 8cm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/4-1652840244.png)
Từ hình vẽ ta có:
Chọn A.
