5 câu hỏi trắc nghiệm thuộc Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 12

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất)

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 12

3693 lượt thi
5 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Thực hiện các phép tính sau:

a) $\frac{- 18}{24} + \frac{15}{- 21}$

b) $9 - 3, 6 - 4, 1 - (- 1, 3)$

Xem đáp án

a, $\frac{- 18}{24} + \frac{15}{- 21} = \frac{- 3}{4} + \frac{- 5}{7} = \frac{- 21}{28} + \frac{- 20}{28}$ $= \frac{- 21 + (- 20)}{28} = \frac{- 41}{28}$

b, $9 - 3, 6 - 4, 1 - (- 1, 3) = 9 - 3, 6 - 4, 1 + 1, 3$

$= (9 + 1, 3) - (3, 6 + 4, 1) = 10, 3 - 7, 7 = 2, 6$

Câu 2:

a) Tìm

x \in ℝ

, biết

|\frac{1}{4} + x| = \frac{5}{6}

b) Tính giá trị của biểu thức

A = {5x}^{2} - 3x - 16

khi x = 2

c) Cho đơn thức

A = 4 x^{2} y^{2} {(- 2 x^{3} y^{2})}^{2}

. Hãy thu gọn và chỉ ra hệ số, phần biến và bậc của đơn thức A.

Xem đáp án

a) $|\frac{1}{4} + x| = \frac{5}{6}$

$\Rightarrow \frac{1}{4} + x = \frac{5}{6}$ hoặc $\frac{1}{4} + x = - \frac{5}{6}$

TH1: $\frac{1}{4} + x = \frac{5}{6} \Rightarrow x = \frac{5}{6} - \frac{1}{4} = \frac{7}{12}$

TH2: $\frac{1}{4} + x = - \frac{5}{6} \Rightarrow x = - \frac{5}{6} - \frac{1}{12} = - \frac{13}{12}$

Vậy $x \in \{\frac{7}{12}; - \frac{13}{12}\}$

b, Thay x = –2 vào biểu thức A = 5x² – 3x – 16, ta được:

A = 5.(–2)² – 3.(–2) – 16 = 5.4 + 6 – 16 = 10

Vậy A = 10 khi x = –2.

A = 4 x^{2} y^{2} {(- 2 x^{3} y^{2})}^{2} = 4 x^{2} y^{2} . {(- 2)}^{2} . {(x^{3})}^{2} . {(y^{2})}^{2}

= 4 x^{2} y^{2} .4. x^{6} . y^{4} = 16 x^{8} y^{6}

Đơn thức A có:

+ Hệ số là 16

+ Phần biến là

x^{8} y^{6}

+ Bậc của đơn thức 14.

Câu 3:

Cho hai đa thức

$f (x) = - {2x}^{2} - {3x}^{3} - 5x + {5x}^{3} - x + x^{2} + 4x + 3 + {4x}^{2}$

$g (x) = {2x}^{2} - x^{3} + 3x + {3x}^{3} + x^{2} - x - 9x + 2.$

a) Tìm $h (x) = f (x) - g (x)$

b) Tìm nghiệm của đa thức h(x).

Xem đáp án

a, $f (x) = - {2x}^{2} - {3x}^{3} - 5x + {5x}^{3} - x + x^{2} + 4x + 3 + {4x}^{2}$

$= (- 3 x^{3} + 5 x^{3}) + (- 2 x^{2} + x^{2} + 4 x^{2}) + (- 5 x - x + 4 x) + 3$

$= 2 x^{3} + 3 x^{2} - 2 x + 3$

$g (x) = {2x}^{2} - x^{3} + 3x + {3x}^{3} + x^{2} - x - 9x + 2.$ $= (- x^{3} + 3 x^{3}) + (2 x^{2} + x^{2}) + (3 x - x - 9 x) + 2$

$= 2 x^{3} + 3 x^{2} - 7 x + 2$

Ta có: $h (x) = f (x) - g (x)$ $= (2 x^{3} + 3 x^{2} - 2 x + 3) - (2 x^{3} + 3 x^{2} - 7 x + 2)$

$= 2 x^{3} + 3 x^{2} - 2 x + 3 - 2 x^{3} - 3 x^{2} + 7 x - 2$

$= (2 x^{3} - 2 x^{3}) + (3 x^{2} - 3 x^{2}) + (- 2 x + 7 x) + (3 - 2)$

$= 5 x + 1$

Ta có h(x) = 0 hay 5x + 1 = 0

$\Rightarrow 5 x = - 1 \Rightarrow x = \frac{- 1}{5}$

Vậy

x = \frac{- 1}{5}

l à n g h i ệ m c ủ a đ a t h ứ c h (x) .

Câu 4:

Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm.

a) Chứng minh tam giác ABC vuông tại A.

b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE ^ BC (E Î BC).

Chứng minh DA = DE.

c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF > DE.

d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC.

Xem đáp án

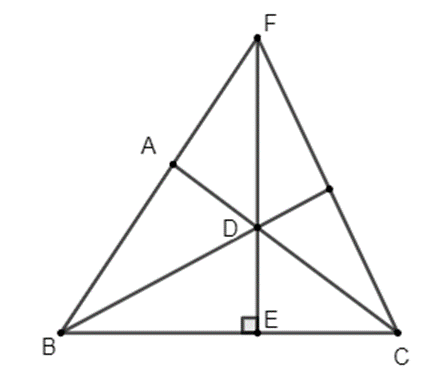
Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm. a) Chứng minh tam giác ABC vuông tại A. b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE  BC (E  BC). Chứng minh DA = DE. c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF > DE. d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC. (ảnh 1)

a) Ta có AB = 6(cm) (gt); AC = 8(cm) (gt) nên

AB² + AC² = 6²+ 8² =100 (cm) (1)

Mà BC = 10(cm) (gt) nên BC² = 10² = 100 (cm) (2)

Từ (1) và (2) suy ra AB² + AC² = BC²

Xét tam giác ABC có AB² + AC² = BC²(chứng minh trên) nên tam giác ABC vuông tại A (Định lí Pytago đảo). (1 điểm)

b) Vì BD là phân giác của góc ABC; DA, DE lần lượt là khoảng cách từ D đến AB, BC

Suy ra DA = DE (tính chất tia phân giác của một góc) (1 điểm)

c) Tam giác ADF vuông tại A nên DF > AD

Lại có AD = DE (chứng minh trên) nên DF > DE (0,5 điểm)

d) Ta có: (tam giác ABD vuông tại A)

(tam giác EBD vuông tại E)

Mà (BD là tia phân giác của góc ABC)

Do đó:

Lại có (hai góc đối đỉnh)

Suy ra

Xét tam giác BDF và tam giác BDC có:

BD cạnh chung

(BD là tia phân giác của góc ABC)

(chứng minh trên)

Do đó: (g.c.g)

BF = BC suy ra B thuộc đường trung trực FC (3)

Và DF = DC suy ra D thuộc đường trung trực FC (4)

Từ (3) và (4) suy ra BD là đường trung trực của FC.

Câu 5:

Cho $f (x) = a x^{3} + b x^{2} + c x + d$ trong đó $a, b, c, d \in ℤ$ và thỏa mãn b = 3a + c. Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.

Xem đáp án

Ta có $f (1) = a + b + c + d .$

Suy ra $f (1) - f (- 2) = 9 a - 3 b + 3 c .$

Mà $b = 3 a + c$ suy ra $f (1) - f (- 2) = 9 a - 3 (3 a + c) + 3 c = 9 a - 9 a - 3 c + 3 c = 0$

$\Rightarrow f (1) = f (- 2) .$

Suy ra $f (1) . f (- 2) = {[f (1)]}^{2} = {(a + b + c + d)}^{2} .$

Mà

a, b, c, d \in ℤ

nên

a + b + c + d \in ℤ

hay

{(a + b + c + d)}^{2}

là bình phương của một số nguyên. Suy ra điều phải chứng minh.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất)

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 12

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương