7 câu hỏi trắc nghiệm thuộc Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 5

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất)

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 5

3781 lượt thi
7 câu hỏi
90 phút

Danh sách câu hỏi

Câu 1:

Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng tần số sau:

Điểm số (x)	3	4	5	6	7	8	9	10
Tần số (n)	1	2	7	8	11	5	2	4	N = 40

a) Dấu hiệu điều tra ở đây là gì? Dấu hiệu có bao nhiêu giá trị khác nhau?

b) Tìm Mốt. Tính số trung bình cộng.

Xem đáp án

a) Dấu hiệu điều tra: “Điểm kiểm tra 1 tiết môn Toán của mỗi học sinh một lớp 7” (0,25 điểm)

Số các giá trị khác nhau là 8. (0,25 điểm)

b) Mốt của dấu hiệu là 7 (vì đây giá trị có tần số lớn nhất: 11) (0,25 điểm)

Số trung bình cộng:

\bar{X} = \frac{3.1 + 4.2 + 5.7 + 6.8 + 7.11 + 8.5 + 9.2 + 10.4}{40} = \frac{269}{40} = 6, 725

Câu 2:

a) Thu gọn đơn thức A. Xác định phần hệ số và tìm bậc của đơn thức thu gọn, biết:

$A = (- \frac{3}{4} x^{2} y^{5} z^{3}) (\frac{5}{3} x^{3} y^{4} z^{2})$

b) Tính giá trị của biểu thức $C = 3 x^{2} y - x y + 6$ tại x = 2, y = 1.

Xem đáp án

A = (- \frac{3}{4} x^{2} y^{5} z^{3}) (\frac{5}{3} x^{3} y^{4} z^{2}) = (- \frac{3}{4} . \frac{5}{3}) . (x^{2} . x^{3}) . (y^{5} . y^{4}) . (z^{3} . z^{2}) = - \frac{5}{4} x^{5} y^{9} z^{5}

Hệ số:

- \frac{5}{4}

Bậc của đơn thức A là 5 + 9 + 5 = 19.

b) Thay x = 2; y = 1 vào biểu thức $C = 3 x^{2} y - x y + 6$

ta được:

Vậy C = 16 tại x = 2 và y = 1. (1 điểm)

Câu 3:

Cho hai đa thức: $M (x) = 3 x^{4} - 2 x^{3} + x^{2} + 4 x - 5$ ; $N (x) = 2 x^{3} + x^{2} - 4 x - 5$

a) Tính $M (x) + N (x)$ ;

b) Tìm đa thức P(x) biết: P(x) + N(x) = M(x).

Xem đáp án

M (x) = 3 x^{4} - 2 x^{3} + x^{2} + 4 x - 5

;

N (x) = 2 x^{3} + x^{2} - 4 x - 5

M (x) + N (x) = 3 x^{4} + (- 2 x^{3} + 2 x^{3}) + (x^{2} + x^{2}) + (4 x - 4 x) + (- 5 - 5)

= 3 x^{4} + 2 x^{2} - 10

Ta có:

P(x) + N(x) = M(x)

Nên $P (x) = M (x) - N (x)$

= (3 x^{4} - 2 x^{3} + x^{2} + 4 x - 5) - (2 x^{3} + x^{2} - 4 x - 5)

= 3 x^{4} + (- 2 x^{3} - 2 x^{3}) + (x^{2} - x^{2}) + (4 x + 4 x) + (- 5 + 5)

= 3 x^{4} - 4 x^{3} + 8 x

Câu 4:

(1.0 điểm) Tìm nghiệm của các đa thức sau:

a, $g (x) = x - \frac{1}{7}$

b, $h (x) = 2 x + 5$

Xem đáp án

a) $g (x) = 0 \Rightarrow x - \frac{1}{7} = 0 \Rightarrow x = \frac{1}{7}$

Vậy là nghiệm của đa thức

g (x)

h (x) = 0 \Rightarrow 2 x + 5 = 0 \Rightarrow x = - \frac{5}{2}

Vậy

x = - \frac{5}{2}

là nghiệm của đa thức

h (x)

Câu 5:

Tìm m để đa thức x = 1. $f (x) = (m - 1) x^{2} - 3 m x + 2$ có một nghiệm

Xem đáp án

f (x) = (m - 1) x^{2} - 3 m x + 2

là một nghiệm của đa thức f(x) nên ta có:

$f (1) = (m - 1) {.1}^{2} - 3 m .1 + 2 = 0$

$\Rightarrow - 2 m + 1 = 0 \Rightarrow m = \frac{1}{2}$

Vậy với

m = \frac{1}{2}

đa thức f(x) có một nghiệm . x =1

Câu 6:

Cho $Δ A B C$ vuông tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và chu vi tam giác ABC.

Xem đáp án

Áp dụng định lý Py–ta–go vào tam giác vuông ABC ta có:

$B C^{2} = A B^{2} + A C^{2}$

$\begin{array}{l} \Rightarrow A C^{2} = B C^{2} - A B^{2} = 10^{2} - 6^{2} = 64 \\ \Rightarrow A C = \sqrt{64} = 8 c m \end{array}$

Chu vi : AB + AC + BC = 6 + 8 + 10 = 24 cm (0,5 điểm)

Câu 7:

Cho $Δ A B C$ vuông tại A, đường phân giác của góc B cắt AC tại D. Vẽ $D H ⊥ B C (H \in B C)$ .

a) Chứng minh: $Δ A B D = Δ H B D$ ;

b) Trên tia đối của AB lấy điểm K sao cho AK = HC. Chứng minh ba điểm K, D, H thẳng hàng.

Xem đáp án

Cho vuông tại A, đường phân giác của góc B cắt AC tại D. Vẽ . a) Chứng minh: ; b) Trên tia đối của AB lấy điểm K sao cho AK = HC. Chứng minh ba điểm K, D, H thẳng hàng. (ảnh 1)

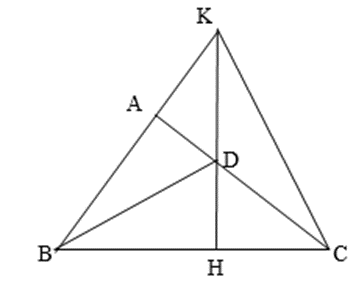
a) Xét hai tam giác vuông ABD và HBD có:

BD là cạnh chung

DA = DH (D nằm trên tia phân giác của góc B)

Do đó: (cạnh huyền – cạnh góc vuông) (1 điểm)

Từ câu a) có

Mà AK = HC (gt)

Nên AB + AK = BH + HC

BK = BC

Suy ra, cân tại B.

Khi đó, BD vừa là phân giác, vừa là đường cao xuất phát từ đỉnh B

là trực tâm của (Do D là giao của hai đường cao BD và AC)

Mặt khác, (c-g-c)

KH là đường cao kẻ từ đỉnh K của nên KH phải đi qua trực tâm D.

Vậy ba điểm K, D, H thẳng hàng.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất)

Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 5

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương