Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 7
-
3673 lượt thi
-
5 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
a) Bậc của đơn thức là gì?
b) Thu gọn và tìm bậc đơn thức sau: –3x2y . 4xy3
Xem đáp án
a) Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó. (0,5 điểm)
b) –3x2y . 4xy3 = (–3.4).(x2.x).(y.y3) = –12x3y4
Bậc của đơn thức –12x3y4 là 3 + 4 = 7. (0,5 điểm)
Câu 2:
a) Phát biểu định lý Py–ta–go;
b) Tìm x trên hình vẽ dưới đây.
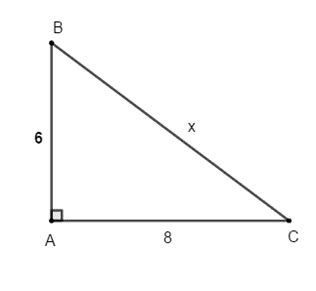
Xem đáp án
a) Định lý Py–ta–go: "Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông." (0,5 điểm)
b)
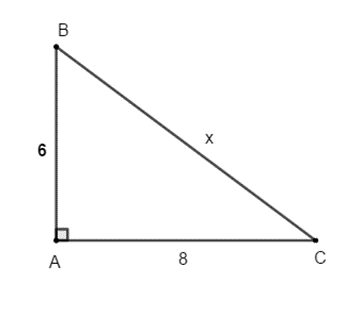
Vì vuông tại A nên theo định lý Py–ta–go ta có:
Hay
Vậy x = 10. (0,5 điểm)
Câu 3:
Thời gian giải xong một bài toán (tính bằng phút) của mỗi học sinh lớp 7 được ghi lại ở bảng sau
|
10 |
13 |
15 |
10 |
13 |
15 |
17 |
17 |
15 |
13 |
|
15 |
17 |
15 |
17 |
10 |
17 |
17 |
15 |
13 |
15 |
a) Dấu hiệu điều tra ở đây là gì? Có bao nhiêu giá trị của dấu hiệu?
b) Lập bảng tần số và tính số trung bình cộng của dấu hiệu. Xem đáp án
a) Dấu hiệu ở đây là thời gian làm một bài toán (tính bằng phút) của mỗi học sinh.
Có 20 giá trị.
b) Bảng “tần số”
|
Giá trị (x) |
10 |
13 |
15 |
17 |
|
|
Tần số (n) |
3 |
4 |
7 |
6 |
N = 20 |
Số trung bình cộng là:
Câu 4:
Cho hai đa thức f(x) = 3x + x3 + 2x2 + 4
g(x) = x3 + 3x + 1 – x2
a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến;
b) Tính f(x) + g(x) và f(x) – g(x);
c) Chứng tỏ f(x) – g(x) không có nghiệm.
Xem đáp án
f(x) = 3x + x3 + 2x2 + 4 = x3 + 2x2 + 3x + 4 (0,5 điểm)
g(x) = x3 + 3x + 1 – x2 = x3 – x2 + 3x + 1 (0,5 điểm)
b,
Ta có: f(x) + g(x) = (x3 + 2x2 + 3x + 4) + (x3 – x2 + 3x + 1)
= x3 + 2x2 + 3x + 4 + x3 – x2 + 3x + 1
= (x3 + x3) + (2x2 – x2) + (3x + 3x) + (4 + 1)
= 2x3 + x2 + 6x +5 (0,5 điểm)
f(x) – g(x) = (x3 + 2x2 + 3x + 4) – (x3 – x2 + 3x + 1)
= x3 + 2x2 + 3x + 4 – x3 + x2 – 3x – 1
= (x3 – x3) + (2x2 + x2) + (3x – 3x) + (4 – 1)
= 3x2 + 3
c,
Vì 3x2 ≥ 0 với mọi x nên 3x2 + 3 ≥ 3 với mọi x
Do đó không tìm được giá trị nào của x để 3x2 + 3 = 0
Vậy f(x) – g(x) = 3x2 + 3 không có nghiệm.
Câu 5:
Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 10cm,
BC = 12cm.
a) Chứng minh ;
b) Tính độ dài đoạn thẳng AH;
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A, G, H thẳng hàng
Xem đáp án
Vẽ đúng hình, ghi GT – KL 0,5 điểm
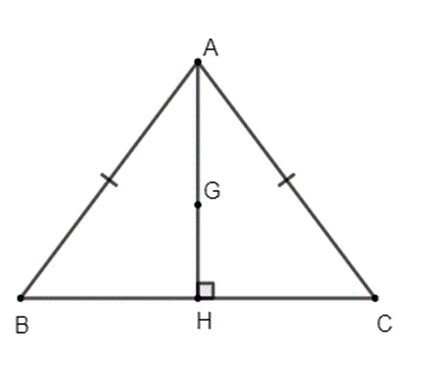
AB = AC (vì ∆ABC cân tại A)
Có cạnh AH chung
Vậy ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)∆ABC cân tại A nên đường cao AH cũng đồng thời là đường trung tuyến từ A mà G là trọng tâm ∆ABC lên G thuộc AH hay 3 điểm A, G, H thẳng hàng. (0,5 điểm)