9 câu hỏi trắc nghiệm thuộc Đề sô 07

Đề thi Toán 7 Giữa kì 1 (có đáp án)

Đề sô 07

3648 lượt thi
9 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giá trị của biểu thức $- 5^{2} + 2018^{0}$ là

A. 26.

B. -25.

C. -24.

D. 1993.

Xem đáp án

Chọn C

Vì $- 5^{2} + 2018^{0} = - 25 + 1 = - 24$

Câu 2:

Từ đẳng thức $9.28 = 63.4$ có thể suy ra tỉ lệ thức nào sau đây

A. $\frac{9}{28} = \frac{63}{4}$

B. $\frac{9}{4} = \frac{63}{28}$

C. $\frac{28}{9} = \frac{4}{63}$

D. $\frac{4}{28} = \frac{9}{63}$

Xem đáp án

Chọn B

Ta có $a . b = c . d \Rightarrow \frac{a}{d} = \frac{c}{b}$

Nên $9.28 = 63.4 \Rightarrow \frac{9}{4} = \frac{63}{28}$

Câu 3:

Giá trị của biểu thức ${(9^{2})}^{3}$ là

A. $9^{6}$

B. $9^{5}$

C. $9^{8}$

D. $3^{12}$

Xem đáp án

Áp dụng công thức ${(a^{m})}^{n} = a^{m . n}$ ư

Nên ${(9^{2})}^{3} = 9^{2.3} = 9^{6}$

Câu 4:

Nếu $|x| = 7$ thì giá trị của $x$ là

A. $x = 7$

B. $x = - 7$

C. $x = \pm 7$

D. $Đ á p á n k h á c$

Xem đáp án

Chọn C

Áp dụng công thức $|a| = b (b \geq 0) \Rightarrow a = b$ hoặc $a = - b$

Nên ta có $|x| = 7 \Rightarrow x = 7$ hoặc $x = - 7$

Câu 5:

(1,5 điểm) Tính hợp lý nếu được:

$a) {(\frac{- 4}{7})}^{25} : {(\frac{- 4}{7})}^{23}$

$b) \frac{15}{60} + \frac{12}{19} + \frac{2}{9} - \frac{10}{8} + \frac{- 31}{19}$

$c) \frac{5^{10} {.7}^{3} - 25^{5} {.49}^{2}}{{(125.7)}^{3} + 5^{9} {.7}^{3} .8}$

Xem đáp án

$a) {(\frac{- 4}{7})}^{25} : {(\frac{- 4}{7})}^{23} = {(\frac{- 4}{7})}^{25 - 23} = {(\frac{- 4}{7})}^{2} = \frac{16}{49}$

$b) \frac{15}{60} + \frac{12}{19} + \frac{2}{9} - \frac{10}{8} + \frac{- 31}{19} = (\frac{12}{19} + \frac{- 31}{19}) + (\frac{1}{4} - \frac{5}{4}) + \frac{2}{9} = 1 - 1 + \frac{2}{9} = \frac{2}{9}$

$c) \frac{5^{10} {.7}^{3} - 25^{5} {.49}^{2}}{{(125.7)}^{3} + 5^{9} {.7}^{3} .8} = \frac{5^{10} {.7}^{3} - 5^{10} {.7}^{4}}{5^{9} {.7}^{3} + 5^{9} {.7}^{3} .8} = \frac{5^{10} 7^{3} (1 - 7)}{5^{9} {.7}^{3} (1 + 8)} = \frac{5. (- 6)}{9} = \frac{- 10}{3}$

Câu 6:

(2,0 điểm) Tìm $x$ biết:

$a) {(\frac{4}{5})}^{x} = \frac{64}{125}$ $c) (- 1 \frac{2}{3} - x) (2 x + \frac{3}{7}) = 0$

$b) |\frac{- 7}{9} + x| - \frac{5}{6} = \frac{1}{18}$ $d) \frac{3 x - 5}{7} = \frac{2 x + 1}{13}$

Xem đáp án

$a) {(\frac{4}{5})}^{x} = \frac{64}{125} \Rightarrow {(\frac{4}{5})}^{x} = {(\frac{4}{5})}^{3} \Rightarrow x = 3 V ậ y x = 3$

$b) |\frac{- 7}{9} + x| - \frac{5}{6} = \frac{1}{18} \Rightarrow |\frac{- 7}{9} + x| = \frac{1}{18} + \frac{5}{6} \Rightarrow |\frac{- 7}{9} + x| = \frac{1}{18} + \frac{15}{18} \Rightarrow |\frac{- 7}{9} + x| = \frac{8}{9} \Rightarrow \frac{- 7}{9} + x = \frac{8}{9} h o ặ c \frac{- 7}{9} + x = - \frac{8}{9} \frac{- 7}{9} + x = \frac{8}{9} \Rightarrow x = \frac{8}{9} + \frac{7}{9} = \frac{15}{9} = \frac{5}{3} \frac{- 7}{9} + x = - \frac{8}{9} \Rightarrow x = - \frac{8}{9} + \frac{7}{9} = \frac{- 1}{9} V ậ y x \in \{\frac{5}{3}; \frac{- 1}{9}\}$

$c) (- 1 \frac{2}{3} - x) (2 x + \frac{3}{7}) = 0 \Rightarrow - 1 \frac{2}{3} - x = 0 h o ặ c 2 x + \frac{3}{7} = 0 +) - 1 \frac{2}{3} - x = 0 \Rightarrow x = \frac{- 5}{3} +) 2 x + \frac{3}{7} = 0 \Rightarrow 2 x = - \frac{3}{7} \Rightarrow x = - \frac{3}{7} : 2 = \frac{- 3}{14} V ậ y x \in \{\frac{- 5}{3}; \frac{- 3}{14}\}$

$d) \frac{3 x - 5}{7} = \frac{2 x + 1}{13} \Rightarrow 13. (3 x - 5) = 7 (2 x + 1) \Rightarrow 39 x - 65 = 14 x + 7 \Rightarrow 25 x = 72 \Rightarrow x = \frac{72}{25} V ậ y x = \frac{72}{25}$

Câu 7:

(1,5 điểm) Trong phong trào thi đua hái hoa điểm tốt, số hoa điểm tốt đạt được của ba bạn Linh, Nga, Hương lần lượt tỉ lệ với

3; 2; 4. Tính số hoa điểm tốt của mỗi bạn biết rằng tổng số hoa đạt được của ba bạn là 72 bông.

Xem đáp án

Gọi số hoa điểm tốt của mỗi bạn Linh, Nga, Hương lần lượt là: $x, y, z (x, y, z \in ℕ *)$

Theo bài ra ta có: $\frac{x}{3} = \frac{y}{2} = \frac{z}{4}; x + y + z = 72$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\frac{x}{3} = \frac{y}{2} = \frac{z}{4} = \frac{x + y + z}{3 + 2 + 4} = \frac{72}{9} = 8

\Rightarrow x = 3.8 = 24 (T M)

\Rightarrow y = 2.8 = 16 (T M)

\Rightarrow z = 4.8 = 32 (T M)

Vậy số hoa điểm tốt của ba bạn Linh, Nga, Hương lần lượt là 24; 16; 32 điểm.

Câu 8:

(2,5 điểm) Cho hình vẽ sau:

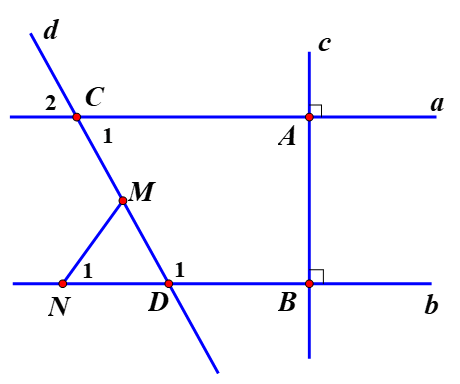
Cho hình vẽ sau: a) Chứng minh a song song với b (ảnh 1)

Biết

a ⊥ c, b ⊥ c, \hat{C_{1}} = 53 °, \hat{N_{1}} = 37 ° .

a) Chứng minh:

a // b

b) Tính số đo

\hat{C_{2}} v à \hat{D_{1}}

c) Chứng minh:

C M ⊥ M N

Xem đáp án

a) Vì

a ⊥ c

và

b ⊥ c

nên

a // b

(tính chất 1)

b) Ta có: $\hat{C_{2}} = \hat{C_{1}} = 53 °$ (hai góc đối đỉnh)

Lại có: $a // b$ (cm câu a)

Nên $\hat{C_{1}} + \hat{D_{1}} = 180 °$ (hai góc trong cùng phía)

$\hat{D_{1}} = 180 ° - \hat{C_{1}} = 180 ° - 53 ° = 127 °$

Vậy $\hat{C_{2}} = 53 °; \hat{D_{1}} = 127 ° .$

c) Kẻ đường thẳng $d'$ qua $M$ song song với $a$

Khi đó $d'// b$ (tính chất 3)

$\hat{M_{1}} = \hat{C_{1}} = 53 °$ (hai góc so le trọng)

$\hat{M_{2}} = \hat{N_{1}} = 37 °$ (hai góc so le trong)

$\Rightarrow \hat{M} = \hat{M_{1}} + \hat{M_{2}} = 53 ° + 37 ° = 90 °$

Vậy $C M ⊥ M N$

Câu 9:

(0,5 điểm) Cho $x, y, z$ là các số thực khác, thỏa mãn:

$P = \frac{x + y - 2017 z}{z} = \frac{y + z - 2017 x}{x} = \frac{z + x - 2017 y}{y}$

Hãy tính giá trị của biểu thức:

P = (1 + \frac{y}{x}) (1 + \frac{x}{z}) (1 + \frac{z}{y})

P = - 1 .

Xem đáp án

Ta có:

$\frac{x + y - 2017 z}{z} = \frac{y + z - 2017 x}{x} = \frac{z + x - 2017 y}{y}$

Suy ra:

$\frac{x + y - 2017 z}{z} + 2018 = \frac{y + z - 2017 x}{x} + 2018 = \frac{z + x - 2017 y}{y} + 2018$

$\Rightarrow \frac{x + y + z}{z} = \frac{y + z + x}{x} = \frac{z + x + y}{y}$

Trường hợp 1: $x + y + z = 0 \Rightarrow x + y = - z; y + z = - x; z + x = - y$

Suy ra : $P = (1 + \frac{y}{x}) (1 + \frac{x}{z}) (1 + \frac{z}{y}) = \frac{x + y}{x} . \frac{z + x}{z} . \frac{y + z}{y} = (\frac{- z}{x}) . (\frac{- y}{z}) . (\frac{- x}{y}) = - 1$

Trường hợp 2: $x + y + z \neq 0 \Rightarrow x = y = z$

Suy ra: $P = (1 + \frac{y}{x}) (1 + \frac{x}{z}) (1 + \frac{z}{y}) = \frac{x + y}{x} . \frac{z + x}{z} . \frac{y + z}{y} = \frac{2 x}{x} . \frac{2 z}{z} . \frac{2 y}{y} = 8$

Vậy $P = 8$ hoặc $P = - 1 .$

Bắt đầu thi ngay

Bài thi liên quan

Đề số 01
- 5 câu hỏi
- 45 phút
Đề số 02
- 8 câu hỏi
- 45 phút
Đề số 03
- 13 câu hỏi
- 60 phút
Đề số 04
- 4 câu hỏi
- 60 phút
Đề số 05
- 5 câu hỏi
- 60 phút
Đề số 06
- 10 câu hỏi
- 60 phút
Đề số 08
- 10 câu hỏi
- 60 phút
Đề số 09
- 10 câu hỏi
- 60 phút
Đề số 10
- 8 câu hỏi
- 60 phút
Đề số 11
- 8 câu hỏi
- 60 phút

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Toán 7 Giữa kì 1 (có đáp án)

Đề sô 07

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương