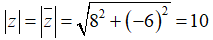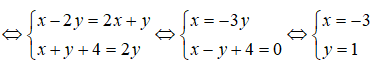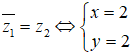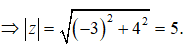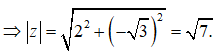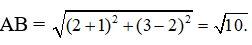16 câu hỏi trắc nghiệm thuộc 16 câu trắc nghiệm: Số phức (có đáp án)

16 câu trắc nghiệm: Số phức (có đáp án)

Đề số 1

16 câu trắc nghiệm: Số phức (có đáp án)

1496 lượt thi
16 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho số phức z = 2 – 2i. Tìm khẳng định sai.

A. Phần thực của z là: 2.

B. Phần ảo của z là: -2.

C. Số phức liên hợp của z là $z = - 2 + 2 i .$

D. Môđun của z là $|z| = \sqrt{2^{2} + {(- 2)}^{2}} = 2 \sqrt{2}$

Xem đáp án

Số phức liên hợp của z = 2 – 2i là $z = 2 + 2 i$ nên khẳng định C là sai.

Chọn đáp án C.

Câu 2:

Cho số phức z = -1 + 3i. Phần thực, phần ảo của $z$ là

A. -1 và 3

B. -1 và -3

C. 1 và -3

D. -1 và -3i

Xem đáp án

Ta có z = -1 + 3i => $z = - 1 - 3 i$

Vậy phần thực và phần ảo của z− là -1 và -3.

Chọn đáp án B.

Câu 3:

Môđun của số phức z thỏa mãn $z = 8 - 6 i$ là

A. 2

B. 10

C. 14

D .7

Xem đáp án

Ta có

Chọn đáp án B.

Câu 4:

Tìm các số thực x, y sao cho $(x - 2 y) + (x + y + 4) . i = (2 x + y) + 2 y i .$

A. x = 3, y = 1

B. x = 3, y = -1

C. x = -3, y = -1

D. x = -3, y = 1

Xem đáp án

Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.

Vậy x = -3, y = 1.

Chọn đáp án D.

Câu 5:

Hai số phức $z_{1} = x - 2 i, z_{2} = 2 + y i$ (x, y ∈ R) là liên hợp của nhau khi

A. x = 2, y = -2

B. x = -2, y = -2

C. x = 2, y = 2

D. x = -2, y = 2

Xem đáp án

Ta có $z_{1} = x + 2 i$ . Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi

Vậy x= 2, y = 2. Chọn đáp án C.

Câu 6:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = |1 + i| là

A. Hai điểm

B. Hai đường thẳng

C. Đường tròn bán kính R=2

D. Đường tròn bán kính $R = \sqrt{2}$

Xem đáp án

Ta có $| 1 + i | = \sqrt{(1 + 1)} = \sqrt{2} .$ Gọi M là điểm biểu diễn của z ta có |z| = OM.

Do đó: $| z | = | 1 + i | \Leftrightarrow O M = \sqrt{2}$ $\Leftrightarrow R = \sqrt{2} .$

Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R = $\sqrt{2}$

Chọn đáp án D.

Câu 7:

Phần thực của số phức z = -i là

A. -1

B. 1

C. 0

D. -i

Xem đáp án

Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0

Chọn C

Câu 8:

Phần ảo của số phức z = -1 là

A. -i

B. 1

C. -1

D. 0

Xem đáp án

Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0

Chọn D

Câu 9:

Số phức liên hợp của số phức z = 1 + i là

A. 1-i

B. -1-i

C. -1+i

D. 1+i

Xem đáp án

Số phức liên hợp của số phức z = 1 + i là z− = 1 - i

Chọn A

Câu 10:

Cho z = 2i -1. Phần thực và phần ảo của $z$ là

A. 2 và 1

B. -1 và -2

C. 1 và 2i

D. -1 và -2i

Xem đáp án

Ta có z = 2i - 1 = -1 + 2i ⇔ $z = - 1 - 2 i$ . Vậy phần thực của $z$ là -1 và phần ảo của $z$ là -2.

Chọn B

Câu 11:

Môđun của số phức z = -3 + 4i là

A. 5

B. -3

C. 4

D. 7

Xem đáp án

Chọn A

Ta có: z = -3 + 4i

Câu 12:

Môđun của số phức $z = 2 - \sqrt{3} i$ là

A. $\sqrt{7}$

B. $2 + \sqrt{3}$

C. $2 - \sqrt{3}$

D. 7

Xem đáp án

Chọn A

Ta có: $z = 2 - \sqrt{3} i$

Câu 13:

Số phức z = 1 - 2i có điểm biểu diễn là

A. M (1; 2)

B. M (1; -2)

C. M (-1; 2)

D. M (-1; -2)

Xem đáp án

Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).

Chọn B

Câu 14:

Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và $z = 1 - i$ đối xứng nhau qua

A. Trục tung

B. Trục hoành

C. Gốc tọa độ

D. Điểm I (1; -1)

Xem đáp án

Hai điểm biểu diễn của z = 1 + i và $z = 1 - i$ là M(1; 1) và N(1; -1) đối xứng với nhau qua trục Ox.

Chọn B

Câu 15:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là

A. Hai đường thẳng

B. Đường tròn bán kính bằng 2

C. Đường tròn bán kính bằng 4

D. Hình tròn bán kính bằng 2

Xem đáp án

Gọi M là diểm biểu diễn của z. Ta có: |z| = 2 ⇔ OM = 2

Vậy quỹ tích của M là đường tròn tâm là gốc tọa độ O và bán kính R = 2.

Chọn B

Câu 16:

Gọi A, B là các điểm biểu diễn của các số phức $z_{1} = - 1 + 2 i, z_{2} = 2 + 3 i .$ Khi đó, độ dài đoạn thẳng AB là

A. $\sqrt{26}$

B. $\sqrt{5} + \sqrt{13}$

C. $\sqrt{10}$

D. 10

Xem đáp án

Chọn C

Ta có: A(-1;2), B(2,3). Do đó:

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

16 câu trắc nghiệm: Số phức (có đáp án)

16 câu trắc nghiệm: Số phức (có đáp án)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương