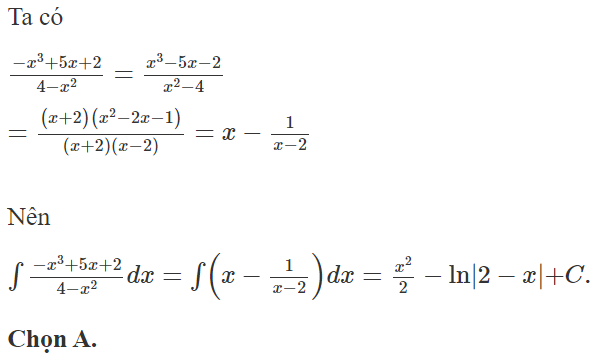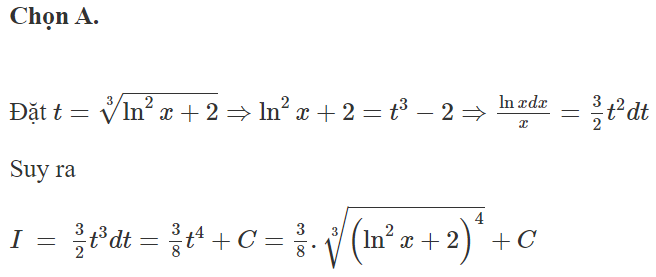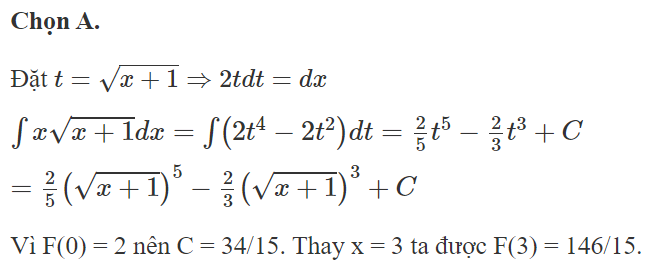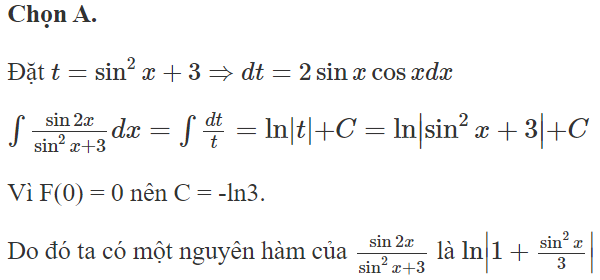30 câu hỏi trắc nghiệm thuộc 150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao-P1 (có đáp án)

Câu 1:

Kết quả tính $\int \frac{- x^{3} + 5 x + 2}{4 - x^{2}} d x$ bằng

A. $\frac{x^{2}}{2} - \ln |2 - x| + C$

B. $\frac{x^{2}}{2} + \ln |2 - x| + C$

C. $\frac{x^{3}}{3} - \ln |2 - x| + C$

D. $\frac{x^{3}}{3} + \ln |x - 2| + C$

Xem đáp án

Câu 2:

Tìm nguyên hàm của hàm số $f (x) = \sin^{3} x . \sin 3 x$ .

A. $\int f (x) d x = \frac{3}{8} (\frac{\sin 2 x}{2} - \frac{\sin 4 x}{4}) - \frac{1}{8} (x - \frac{\sin 6 x}{6}) + C$

B. $\int f (x) d x = \frac{3}{8} (\frac{\sin 2 x}{2} - \frac{\sin 4 x}{4}) + \frac{1}{8} (x - \frac{\sin 6 x}{6}) + C$

C. $\int f (x) d x = \frac{1}{8} (\frac{\sin 2 x}{2} - \frac{\sin 4 x}{4}) - \frac{3}{8} (x - \frac{\sin 6 x}{6}) + C$

D. $\int f (x) d x = \frac{3}{8} (\frac{\sin 2 x}{2} + \frac{\sin 4 x}{4}) - \frac{1}{8} (x + \frac{\sin 6 x}{6}) + C$

Xem đáp án

Chọn A.

Câu 3:

Họ nguyên hàm của hàm số $f (x) = \frac{x^{2} + x + x^{3} + 1}{x^{3}}$ là hàm số nào?

A. $F (x) = \ln |x| - \frac{1}{x} + x - \frac{1}{2 x^{2}} + C$

B. $F (x) = \ln |x| + \frac{1}{x} + x - \frac{1}{2 x^{2}} + C$

C. $F (x) = \frac{x^{3}}{3} - \frac{3 x^{2}}{2} + \ln |x| + C$

D. $F (x) = \frac{x^{3}}{3} + \frac{3 x^{2}}{2} + \ln |x| + C$

Xem đáp án

Chọn A.

Câu 4:

Giá trị m để hàm số $F (x) = m x^{3} + (3 m + 2) x^{2} - 4 x + 3$ là một nguyên hàm của hàm số $f (x) = 3 x^{2} + 10 x - 4$

A. m = 1.

B. m = 0.

C. m = 2.

D. m = 3.

Xem đáp án

Chọn A.

$\int (3 x^{2} + 10 x - 4) d x = x^{3} + 5 x^{2} - 4 x + C$ , nên m = 1.

Câu 5:

Gọi F(x) là nguyên hàm của hàm số $f (x) = \sin^{4} (2 x)$ thoả mãn F(0) = 3/8. Khi đó F(x) là:

A. $F (x) = \frac{3}{8} (x + 1) - \frac{1}{8} \sin 4 x + \frac{1}{64} \sin 8 x$

B. $F (x) = \frac{3}{8} x - \frac{1}{8} \sin 4 x + \frac{1}{64} \sin 8 x$

C. $F (x) = \frac{3}{8} x - \frac{1}{8} \sin 2 x + \frac{1}{64} \sin 4 x + \frac{3}{8}$

D. $F (x) = x - \sin 4 x + \sin 6 x + \frac{3}{8}$

Xem đáp án

Chọn A.

Vì F(0) = 3/8 nên suy ra đáp án A.

Câu 6:

Biết hàm số $f (x) = {(6 x + 1)}^{2}$ có một nguyên hàm là $F (x) = a x^{3} + b x^{2} + c x + d$ thoả mãn điều kiện F(-1) = 20. Tính tổng $a + b + c + d$

A. 46.

B. 44.

C. 36.

D. 54.

Xem đáp án

Chọn A.

$\int {(6 x + 1)}^{2} d x = \int (36 x^{2} + 12 x + 1) d x = 12 x^{3} + 6 x^{2} + x + C$ nên a = 12; b = 6; c = 1

Thay F(-1) = 20 $\Rightarrow$ d = 27

Ta có: a + b + c + d = 46.

Câu 7:

Tìm nguyên hàm: $I = \int \frac{d x}{e^{x} + 2 e^{- x} - 3}$

A. $\ln |\frac{e^{x} + 2}{e^{x} + 1}| + C$

B. $\ln |\frac{e^{x} + 2}{e^{x} - 1}| + C$

C. $\ln |\frac{e^{x} - 2}{e^{x} + 1}| + C$

D. $\ln |\frac{e^{x} - 2}{e^{x} - 1}| + C$

Xem đáp án

Chọn D.

Ta có: $I = \int \frac{e^{x} d x}{e^{2 x} - 3 e^{x} + 2}$

Đặt $t = e^{x} \Rightarrow d t = e^{x} d x$

Suy ra:

Câu 8:

Tìm nguyên hàm của hàm số $I = \int \frac{\ln x . d x}{x (1 + \sqrt{3 \ln x + 2})}$ với t = $\sqrt{3 \ln x + 2}$

A. $\frac{2}{9} (\frac{t^{3}}{3} + \frac{t^{2}}{2} - t + \ln (t + 1)) + C$

B. $\frac{2}{9} (\frac{t^{3}}{3} - \frac{t^{2}}{2} - t + \ln (t + 1)) + C$

C. $\frac{2}{9} (\frac{t^{3}}{3} - \frac{t^{2}}{2} - t + \ln (t - 1)) + C$

D. $\frac{2}{9} (\frac{t^{3}}{3} - \frac{t^{2}}{2} - t - \ln (t + 1)) + C$

Xem đáp án

Chọn B.

Đặt $t = \sqrt{3 \ln x + 2} \Rightarrow \ln x = \frac{t^{2} - 2}{3} \Rightarrow \frac{d x}{x} = \frac{2}{3} t d t$

Suy ra

với

Câu 9:

Tìm nguyên hàm: $\int \frac{\ln^{2} x + 1}{x} d x$

A. $\frac{\ln^{3} x + \ln x + C}{2}$

B. $\frac{\ln^{3} x + 3 \ln x + C}{2}$

C. $\frac{\ln^{3} x - \ln x + C}{2}$

D. $\frac{3 \ln^{3} x + \ln x + C}{2}$

Xem đáp án

Chọn B.

Đặt $t = \ln x \Rightarrow d t = \frac{d x}{x}$

Suy ra

$= \frac{\ln^{3} x + 3 \ln x + C}{3}$

Câu 10:

Tìm nguyên hàm: $K = \int \frac{\ln x \sqrt[3]{2 + \ln^{2} x}}{x} d x .$

A. $\frac{3}{8} \sqrt[3]{{(\ln^{2} x + 2)}^{4}} + C$

B. $\frac{3}{8} \sqrt[3]{{(3 \ln x - 2)}^{4}} + C$

C. $\frac{3}{8} \sqrt[3]{{(2 \ln x - 2)}^{4}} + C$

D. $\frac{3}{8} \sqrt[3]{{(\ln x + 2)}^{4}} + C$

Xem đáp án

Câu 11:

Tìm nguyên hàm của $I = \int \frac{d x}{2 \sin^{2} x - 3 \sin 2 x + 2}$ .

A. $\frac{1}{2} \ln |\frac{t - 1}{2 \tan x - 1}| + C$

B. $\frac{1}{2} \ln |\tan x| + C$

C. $\frac{1}{2} \ln |\tan 2 x| + C$

D. Đáp án khác

Xem đáp án

Chọn D

Ta có:

Đặt $t = \tan x \Rightarrow d t = \frac{d x}{\cos^{2} x}$

Ta được:

Câu 12:

Tìm nguyên hàm của: $J = \int \frac{d x}{2 \cos x - \sin x + 1}$

A. $\frac{1}{2} \ln |\tan \frac{x}{2}| - x + C$

B. $\frac{1}{2} \ln |\tan \frac{x}{2} + 4| - \ln x + C$

C. $\frac{1}{2} \ln |\tan \frac{x}{2} + 3| - 2 x + C$

D. Đáp án khác

Xem đáp án

Chọn D

Đặt $t = \tan \frac{x}{2} \Rightarrow d x = \frac{2 d t}{1 + t^{2}}, \sin x = \frac{2 t}{1 + t^{2}}, \cos x = \frac{1 - t^{2}}{1 + t^{2}}$

Suy ra:

Câu 13:

Tìm nguyên hàm: $I = \int \frac{\sin^{4} 2 x . c o s^{3} x}{\tan (x + \frac{π}{4}) \tan (x - \frac{π}{4})} d x$ .

A. $16 (\frac{\sin^{11} x}{11} - \frac{\sin^{9} x}{3} + \frac{3 \sin^{7} x}{7} - \frac{\sin^{5} x}{5} + C)$

B. $16 (\frac{\sin^{11} x}{11} + \frac{\sin^{9} x}{3} + \frac{\sin^{7} x}{7} - \frac{\sin^{5} x}{5} + C)$

C. $16 (\frac{\sin^{11} x}{11} - \frac{\sin^{9} x}{3} + \frac{\sin^{7} x}{7} + \frac{\sin^{5} x}{5} + C)$

D. Tất cả đều sai

Xem đáp án

Chọn A

Ta có:

Suy ra: $I = - 16 \int \sin^{4} x . \cos^{6} x . \cos x d x$

Đặt t = sinx => dt = cosxdx nên ta có:

Câu 14:

Tìm nguyên hàm: $I = \int \frac{e^{x} d x}{e^{x} + 4 e^{- x}}$ .

A. $\frac{1}{2} x + \frac{1}{2} \ln |e^{x} + 4 e^{- x}| + C$

B. $\frac{1}{2} x + \ln e^{x} + 4 e + C$

C. $\frac{1}{2} + \frac{1}{3} \ln e^{x} + 4 e^{- x} + C$

D. Đáp án khác

Xem đáp án

Chọn A.

Xét $J = \int \frac{e^{- x} d x}{e^{x} + 4 e^{- x}}$

Ta xét hệ :

hay $I = \frac{1}{2} x + \frac{1}{2} \ln |e^{x} + 4 e^{- x}| + C$

Câu 15:

Tìm nguyên hàm $J = \int \frac{(\ln x + 1) \ln x}{{(\ln x + 1 + x)}^{3}} d x$ .

A. $\frac{x^{2}}{2 \ln x - 1 + x} - \frac{x}{2 (\ln x + x)} + C$

B. $\frac{x^{2}}{2 \ln x - 1 - x} - \frac{x}{2 (\ln x + 2 x)} + C$

C. $\frac{x^{2}}{2 \ln x - 1 + x} + 2 \frac{x}{2 (\ln x + x)} + C$

D. Đáp án khác

Xem đáp án

Chọn D.

Ta có : $J = \int \frac{\ln x + 1}{x {(\frac{\ln x + 1}{x} + 1)}^{3}} . \frac{\ln x}{x^{2}} d x$

Đặt $t = \frac{\ln x + 1}{x} \Rightarrow d t = - \frac{\ln x}{x^{2}} d x$

Suy ra

Câu 16:

Tìm nguyên hàm: $I = \int \frac{x^{3} - 1}{x (x^{6} + 3 x^{3} + 2)} d x .$

A. $- \frac{3}{2} \ln |x^{3} + 2| - \frac{1}{2} \ln |x^{3}| - 2 \ln |x^{3} + 1| + C$

B. $- \ln |x^{3} + 2| - \frac{1}{2} \ln |x^{3}| + 2 \ln |x^{3} + 1| + C$

C. $- \frac{1}{2} \ln |x^{3} + 2| - \frac{1}{6} \ln |x^{3}| + \frac{2}{3} \ln |x^{3} + 1| + C$

D. $- \frac{3}{2} \ln |x^{3} + 2| - \frac{1}{2} \ln |x^{3}| + 2 \ln |x^{3} + 1| + C$

Xem đáp án

Chọn C.

Đặt $t = x^{3} \Rightarrow d t = 3 x^{2} d x$

Khi đó ta có:

+ Thực hiện đồng nhất thức ta có:

Khi đó

Câu 17:

Tìm nguyên hàm: $J = \int \frac{d x}{x {(x^{6} + 1)}^{2}} .$

A. $\frac{1}{6} \ln |\frac{x^{6}}{x^{6} + 1}| + \frac{1}{x^{6} + 1} + C$

B. $\ln |\frac{x^{6}}{x^{6} + 1}| + \frac{1}{x^{6} + 1} + C$

C. $\frac{1}{6} \ln |\frac{x^{6}}{x^{6} + 1}| - 2 \frac{1}{x^{6} + 1} + C$

D. $\frac{1}{6} \ln |\frac{x^{6}}{x^{6} + 1}| - 5 \frac{1}{x^{6} + 1} + C$

Xem đáp án

Chọn A.

Đặt

Suy ra

Câu 18:

Hàm số $f (x) = x \sqrt{x + 1}$ có một nguyên hàm là F(x). Nếu F(0) = 2 thì F(3) bằng

A. $\frac{146}{15}$

B. $\frac{116}{15}$

C. $\frac{886}{105}$

D. $\frac{105}{886}$

Xem đáp án

Câu 19:

Gọi F(x) là một nguyên hàm của hàm số f(x) = xcosx thỏa mãn F(0) = 1. Khi đó phát biểu nào sau đây đúng?

A. F(x) là hàm số chẵn.

B. F(x) là hàm số lẻ.

C. Hàm số F(x) tuần hoàn với chu kì là $π$ .

D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.

Xem đáp án

Chọn A.

$\int x \cos x d x = x \sin x + \cos x + C$

F(0) = 1 nên C = 0. Khi đó F(x) = x.sinx + cosx

Do đó g(x) = x.sinx là hàm số chẵn; h(x)=cos x là hàm số chẵn nên F(x)= g(x) + h(x) là hàm số chẵn.

Câu 20:

Một nguyên hàm F(x) của hàm số $f (x) = \frac{\sin 2 x}{\sin^{2} x + 3}$ thỏa mãn F(0) = 0 là

A. $\ln |1 + \frac{\sin^{2} x}{3}|$

B. $\ln |1 + s i n^{2} x|$

C. $\frac{\ln |2 + \sin^{2} x|}{3}$

D. $\ln |\cos^{2} x|$

Xem đáp án

Câu 21:

Tìm nguyên hàm: $I = \int \sin x . \ln (\cos x) d x$

A. –cosxln(cosx)-cosx+C

B. cosx. lnsinx +sinx +C

C.-sinx.ln(cosx)-cosx+C

D. sinx.ln(sinx)-sinx+C

Xem đáp án

Chọn A.

Đặt $\{\begin{cases} u = \ln (\cos x) \\ d v = \sin x d x \end{cases}$

ta chọn $\{\begin{cases} d u = \frac{- \sin x}{\cos x} d x \\ v = - \cos x \end{cases}$

Suy ra

Câu 22:

Tìm nguyên hàm: $J = \int x \ln \frac{x - 1}{x + 1} d x$

A. $\frac{1}{2} x^{2} \ln \frac{x - 1}{x + 1} - 2 \ln |x + 1| + 2 \frac{1}{x + 1} + C$

B. $\frac{1}{2} x^{2} \ln \frac{x - 1}{x + 1} + 12 \ln |x + 1| - \frac{1}{x + 1} + C$

C. $\frac{1}{2} x^{2} \ln \frac{x - 1}{x + 1} - x - \frac{1}{2} \ln |\frac{x - 1}{x + 1} + C|$

D. Đáp án khác

Xem đáp án

Chọn C.

Câu 23:

Cho $f (x) = \frac{4 m}{π} + \sin^{2} x$ .Tìm m để nguyên hàm của hàm số f(x) thỏa mãn F(0)=1 và $F (\frac{π}{4}) = \frac{π}{8}$

A. -3/4

B. 3/4

C. -4/3

D. 4/3

Xem đáp án

Vì F(0) = 1 nên C =1

$F (\frac{π}{4}) = \frac{π}{8}$ nên tính được m = -3/4

Chọn A.

Câu 24:

Tìm nguyên hàm của hàm số $f (x) = \frac{1}{\sin x . \cos x}$ .

A. $\int f (x) d x = \ln |\sin x| - \frac{1}{2} \ln |1 - \sin^{2} x| + C$

B. $\int f (x) d x = \ln |\sin x| + \frac{1}{2} \ln |1 - \sin^{2} x| + C$

C. $\int f (x) d x = \frac{1}{2} \ln |\sin x| - \frac{1}{2} \ln |1 - \sin^{2} x| + C$

D. $\int f (x) d x = - \ln |\sin x| - \frac{1}{2} \ln |1 - \sin^{2} x| + C$

Xem đáp án

Chọn A

Câu 25:

Tìm nguyên hàm của hàm số $f (x) = \frac{2 \sin^{3} x}{1 + \cos x} .$

A. $\int f (x) d x = \cos^{2} x - 2 \cos x + C$

B. $\int f (x) d x = \frac{1}{2} \cos^{2} x - 2 \cos x + C$

C. $\int f (x) d x = \cos^{2} x + \cos x + C$

D. $\int f (x) d x = \frac{1}{2} \cos^{2} x + 2 \cos x + C$

Xem đáp án

Chọn A

Câu 26:

Tìm nguyên hàm của hàm số $f (x) = \frac{\cos^{3} x}{\sin^{5} x} .$

A. $\int f (x) d x = \frac{c o t^{4} x}{4} + C$

B. $\int f (x) d x = \frac{- c o t^{4} x}{4} + C$

C. $\int f (x) d x = \frac{c o t^{2} x}{2} + C$

D. $\int f (x) d x = \frac{\tan^{4} x}{4} + C$

Xem đáp án

Chọn B.

Câu 27:

Tìm nguyên hàm của hàm số: $f (x) = \cos 2 x (\sin^{4} x + \cos^{4} x) .$

A. $\int f (x) d x = \frac{1}{2} \sin 2 x - \frac{1}{12} \sin^{3} 2 x + C .$

B. $\int f (x) d x = \frac{1}{2} \sin 2 x + \frac{1}{12} \sin^{3} 2 x + C .$

C. $\int f (x) d x = \sin 2 x - \frac{1}{4} \sin^{3} 2 x + C .$

D. $\int f (x) d x = \frac{1}{2} \sin 2 x - \frac{1}{4} \sin^{3} 2 x + C .$

Xem đáp án

Chọn A

Câu 28:

Tìm nguyên hàm của hàm số $f (x) = (\tan x + e^{2 \sin x}) \cos x .$

A. $\int f (x) d x = - \cos x + \frac{1}{2} e^{2 \sin x} + C$

B. $\int f (x) d x = \cos x + \frac{1}{2} e^{2 \sin x} + C$

C. $\int f (x) d x = - \cos x + e^{2 \sin x} + C$

D. $\int f (x) d x = - \cos x - \frac{1}{2} e^{2 \sin x} + C$

Xem đáp án

Chọn A

Câu 29:

Tìm nguyên hàm: $I = \int \frac{x^{4} d x}{{(x^{2} - 1)}^{2}}$

A. $\frac{x^{3}}{2 (x^{2} - 1)} - \frac{3}{2} (x + \frac{1}{2} \ln |\frac{x - 1}{x + 1}|) + C$

B. $\frac{x^{3}}{2 (x^{2} - 1)} + \frac{3}{2} (x + \frac{1}{2} \ln |\frac{x - 1}{x + 1}|) + C$

C. $- \frac{x^{3}}{2 (x^{2} - 1)} + \frac{3}{2} (x + \frac{1}{2} \ln |\frac{x - 1}{x + 1}|) + C$

D. $\frac{x^{3}}{2 (x^{2} + 1)} - \frac{3}{2} (x + \frac{1}{2} \ln |\frac{x - 1}{x + 1}|) + C$

Xem đáp án

Chọn C.

Đặt suy ra

Câu 30:

Tìm nguyên hàm của hàm số $f (x) = \frac{1}{\sin x + \cos x + \sqrt{2}}$ .

A. $\int f (x) d x = - \frac{1}{\sqrt{2}} c o t (\frac{x}{2} + \frac{3 π}{8}) + C$

B. $\int f (x) d x = \frac{1}{\sqrt{2}} c o t (\frac{x}{2} + \frac{3 π}{8}) + C$

C. $\int f (x) d x = - \frac{1}{\sqrt{2}} c o t (\frac{x}{2} + \frac{3 π}{4}) + C$

D. $\int f (x) d x = - \frac{1}{\sqrt{2}} c o t (\frac{x}{2} - \frac{3 π}{8}) + C$

Xem đáp án

Chọn A

CHỌN BỘ SÁCH BẠN MUỐN XEM

150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao (có đáp án)

150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao-P1 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương