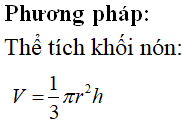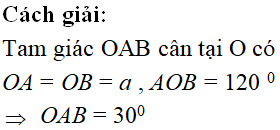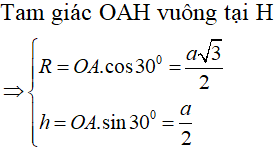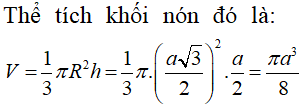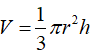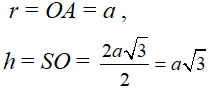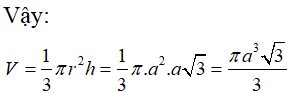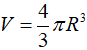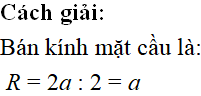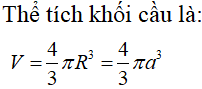160 bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
921 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3). Phương trình của mặt cầu có tâm I và đi qua A là:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Có
Khi đó mặt cầu tâm I đi qua A có phương trình
Câu 2:
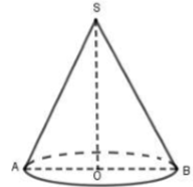
Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Có
Khi đó thể tích khối nón là:
Câu 3:
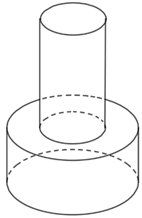
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là thỏa mãn (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng thể tích của khối trụ (H1) bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Thể tích khối trụ (H1) là:
Thể tích khối trụ (H2) là:
Theo giả thiết ta có:
Câu 4:
Cho hình nón có độ dài đường sinh gấp đôi chiều cao và bán kính đáy bằng . Diện tích xung quanh của hình nón đã cho bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Có
Câu 5:
Hai hình nón bằng nhau có chiều cao bằng 2 dm, được đặt như hình vẽ bên (mỗi hình đều đặt thẳng đứng với đỉnh nằm phía dưới). Lúc đầu, hình nón trên chứa đầy nước và hình nón dưới không chứa nước. Sau đó, nước được chảy xuống hình nón dưới thông qua lỗ trống ở đỉnh của hình nón trên. Hãy tính chiều cao của nước trong hình nón dưới tại thời điểm khi mà chiều cao của nước trong hình nón trên bằng 1 dm.

 Xem đáp án
Xem đáp án
Chọn đáp án A.
Lượng nước trong nón 1 đã chảy xuống nón 2 bằng:
Chiều cao nước nón 2 là h thì bán kính đáy nước trong nón 2 bằng:
Thể tích nước trong nón 2 bằng:
Câu 6:
Cho hình chữ nhật ABCD có AB = 2AD. Quay hình chữ nhật đã cho quanh AD và AB ta được hai hình trụ tròn xoay có thể tích lần lượt là V1, V2. Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Quay quanh AD thu được trụ có r = AB, h = AD; quay quanh AB thu được trụ có r = AD, h = AB.
Vậy
Câu 7:
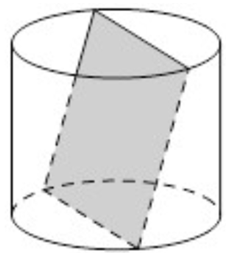
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Hộp hình trụ có R = h = 10. Gọi a là độ dài cạnh hình vuông (tấm bìa) đã cho. Gọi AB, CD lần lượt là cạnh hình vuông trên mặt đáy; cạnh trên mặt phía trên của hộp. Gọi E, F lần lượt là hình chiếu vuông góc của C, D xuống mặt đáy.
Ta có:
Do đó
Mặt khác theo pitago có:
Từ (1) và (2) có:
Câu 8:
Mặt cầu ngoại tiếp tứ diện vuông O.ABC có OA = OB = OC = a có bán kính bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Có
Câu 9:
Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần Stp của hình nón khi quay tam giác ABC xung quanh trục AC.
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Nón có:
Câu 10:
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ?
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Theo giả thiết thể tích khối cầu đá bằng thể tích khối trụ.
Do vậy:
Câu 11:
Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Tính góc α ở đỉnh của hình nón.
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có:
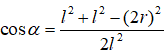
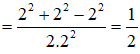
Câu 12:
Cho hình chóp S.ABC có SA=SB=SC=a, , . Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Ta có:
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có:
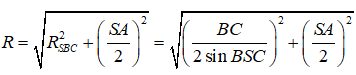
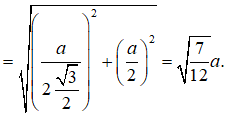
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và AB=2, AC=4,SA= . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Bán kính mặt cầu ngoại tiếp tứ diện vuông S.ABC đỉnh A là:
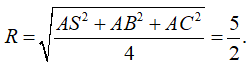
Câu 14:
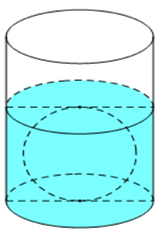
Người ta thả một viên bi sắt có dạng hình cầu với bán kính nhỏ hơn 4,5cm vào một chiếc cốc hình trụ đang chứa nước thì viên bi sắt đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong lòng cốc bằng 4,5cm. Bán kính của viên bi sắt đó bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Thể tích khối nước trong cốc là:
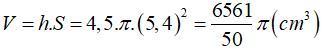
Thể tích của khối cầu là .
Sau khi thả viên bi, chiều cao của mực nước bằng đường kính khối cầu nên tổng thể tích của nước và khối cầu là:
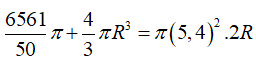
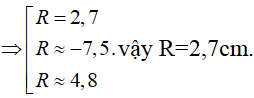
Câu 15:
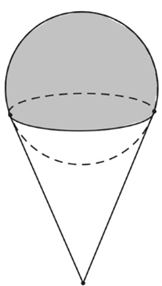
Một que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Thể tích kem đóng băng:
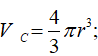
Thể tích kem sau khi tan chảy:
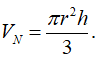
Theo giả thiết có:
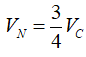
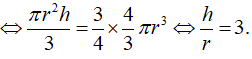
Câu 16:
Một chiếc kem gồm hai phần: phần phía dưới là một khối nón có chiều cao gấp đôi bán kính đáy; phần phía trên là một nửa khối cầu có đường kính bằng đường kính đáy của khối nón bên dưới. Thể tích phần kem phía trên bằng 200cm3 , thể tích của cả chiếc kem đã cho bằng:
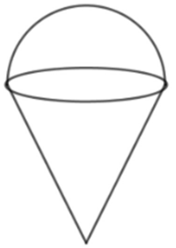
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Có thể tích phần kem phía trên bằng thể tích nửa khối cầu và bằng:
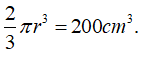
Thể tích phần kem phía dưới bằng :
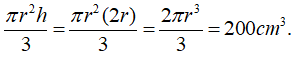
Thể tích của cả chiếc kem bằng 400cm3
Câu 17:
Cho tam giác ABC vuông tại A, AB=6, AC=8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là:
 Xem đáp án
Xem đáp án
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.

Trong , gọi là H chân đường cao của A đến BC. Ta có:
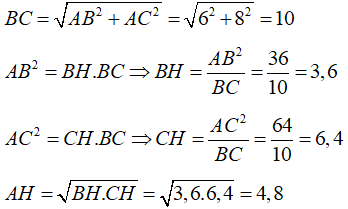
Thể tích hình nón đỉnh C là:
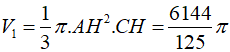
Thể tích hình nón đỉnh B là:
![]()
Khối tròn xoay có thể tích:
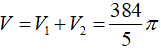
Câu 18:
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R), (O',R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O'AB là tam giác đều và (O'AB) hợp với đường tròn O một góc . Tính diện tích xung quanh của hình trụ.
 Xem đáp án
Xem đáp án
Đáp án D
Gọi I là trung điểm của AB, ta có
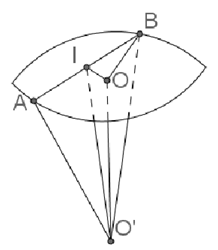
Đặt OI=x ta có:
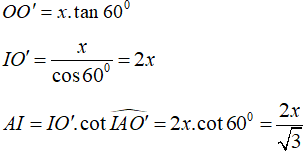
![]()
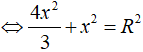
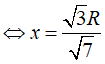
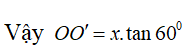
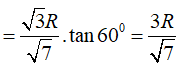
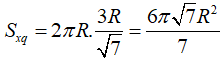
Câu 19:
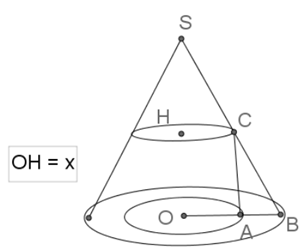
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h, OB=R, OH=x ( 0<x<h). Tìm thể tích lớn nhất của hình trụ.
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
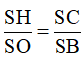
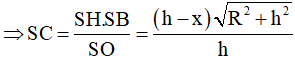
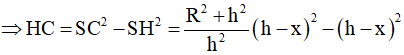
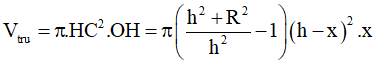
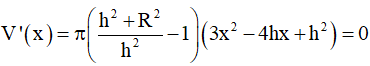
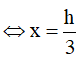
Vậy thể tích lớn nhất của hình trụ là:
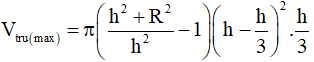
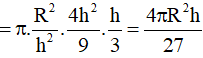
Câu 20:
Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy 1 góc . Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
 Xem đáp án
Xem đáp án
Đáp án A.
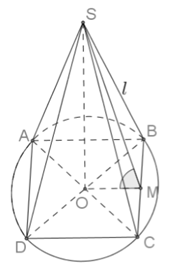
Gọi M là trung điểm của BC, suy ra:
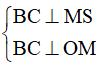
![]()
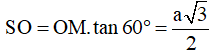
Gọi l, R lần lượt là đường sinh và bán kính của hình nó ngoại tiếp hình chóp, khi đó:
![]()
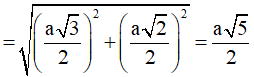
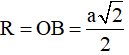
Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
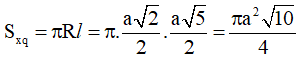
Câu 21:
Cắt một hình nón bởi mặt phẳng qua trục được thiết diện một tam giác vuông cân có cạnh huyền bằng 2. Diện tích toàn phần của hình nón là?
 Xem đáp án
Xem đáp án
Đáp án A.
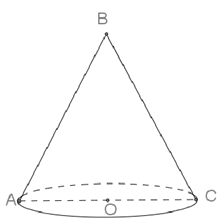
Thiết diện là tam giác vuông cân tại đình B, cạnh huyền AC=2 .
Đặt BA=BC=x, ta có:
![]()
Diện tích toàn phần của hình nón là:
![]()
Câu 22:
Một hình trụ có tâm các đáy là O, O’. Biết rằng mặt cầu đường kính OO’ tiếp xúc với các mặt đáy của hình trụ tại O, O’ và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là . Tính diện tích xung quanh của hình trụ đã cho.
 Xem đáp án
Xem đáp án
Đáp án A.
Theo bài ra ta có chiều cao của hình trụ bằng đường kính đáy của hình trụ và bằng đường kính của mặt cầu.
Gọi bán kính của mặt cầu là R, ta có:
![]()
Vậy hình trụ có bán kính , chiều cao .
Diện tích xung quanh của hình trụ:
![]()
Câu 23:
Người ta cần đổ một ống thoát nước hình trụ bằng bê tông với chiều cao 100cm, độ dày của thành ống là 10cm và đường kính của ống là 50cm. Lượng bê tông cần phải đổ là:
 Xem đáp án
Xem đáp án
Đáp án A.
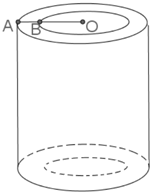
Thể tích lượng bê tông cần dùng chính bằng thể tích của hình trụ bán kính OA (V1) trừ thể tích hình trụ bán kính OB (V2). Ta có:
![]()
![]()
![]()
Vậy lượng bê tông cần dùng là:
![]()
Câu 24:
Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD.
 Xem đáp án
Xem đáp án
Đáp án D.
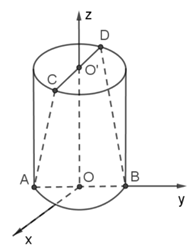
Gắn hệ trục tọa độ như hình vẽ, khi đó:
![]()
![]()
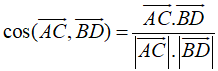
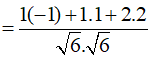
![]()
Do đó cosin góc giữa 2 đường thẳng AC và BD là .
Câu 25:
Trong không gian cho tam giác ABC vuông tại B, BC=a, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
 Xem đáp án
Xem đáp án
Đáp án B.
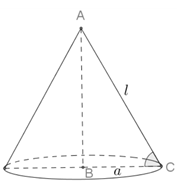
Khi quay tam giác ABC quanh cạnh AB, ta được khối nón có đỉnh A, đường sinh:
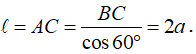
Diện tích xung quanh của hình nón là:
![]()
Câu 26:
Người ta bỏ vào một chiếc hộp hình trụ ba quả bóng tennis hình cầu bằng nhau, biết rằng đáy hình trụ bằng hình tròn lớn trên quả bóng, chiều cao của hình trụ gấp 3 lần đường kính quả bóng. Gọi V1 là tổng thể tích ba quả bóng, V2 là thể tích của hình trụ. Khi đó tỉ số là:
 Xem đáp án
Xem đáp án
Đáp án D.

Gọi r là bán kính của một quả bóng.
Khi đó thể tích của một quả nóng là .
Suy ra:
![]()
Thể tích hình trụ:
![]()
Do đó =
Câu 27:
Cho một khối trụ có độ dài đường sinh bằng 10cm. Biết thể tích khối trụ bằng . Diện tích xung quanh của khối trụ bằng:
 Xem đáp án
Xem đáp án
Chọn D.
Phương pháp:
Hình trụ có bán kính đáy r và có chiều cao h thì có diện tích xung quanh và có thể tích . (Với khối trụ thì đường sinh và chiều cao bằng nhau)
Cách giải:
Gọi r là bán kính đáy, theo đề bài ta có:
![]()
![]()
![]()
Diện tích xung quanh hình trụ là:
![]()
Câu 28:
Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho.
 Xem đáp án
Xem đáp án
Chọn A.
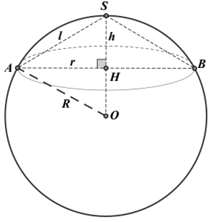
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Suy ra: ![]()
Góc ở đỉnh của hình nón là nên suy ra (như hình vẽ).
Trong tam giác OAH vuông tại H ta có:
![]()
![]()
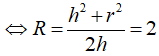
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Cách 2:
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Trong tam giác SAH vuông tại H ta có:
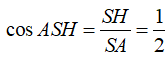
![]()
Xét tam giác SOA có OS=OA=R và OSA=
Suy ra tam giác SOA đều.
Do đó R=OA=SA=2.
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Câu 29:
Cắt mặt xung quanh của một hình trụ dọc theo một đường sinh rồi trải ra trên một mặt phẳng ta được hình vuông có chu vi bằng . Thể tích của khối trụ đã cho bằng:
 Xem đáp án
Xem đáp án
Chọn A.
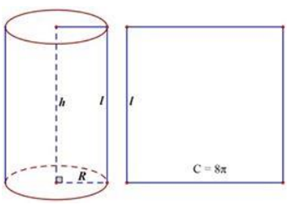
Ta có chu vi hình vuông bằng cạnh hình vuông bằng
Do đó hình trụ có bán kính R=1, đường sinh l= (cũng chính là đường cao).
Vậy thể tích hình trụ:
![]()
Câu 30:
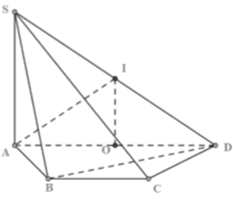
Cho hình chóp S.ABCD đáy là hình thang cân có AB=BC=CD. Cạnh bên SA vuông góc với đáy, SA=2a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD là:
 Xem đáp án
Xem đáp án
Chọn A.
Phương pháp:
Cách xác định tâm mặt cầu ngoại tiếp khối chóp:
- Xác định tâm O của đường tròn ngoại tiếp đa giác đáy
- Từ O dựng đường thẳng d vuông góc với mặt phẳng đáy
- Dựng mặt phẳng trung trực của một cạnh bên nào đó
- Xác định . I chính là tâm mặt cầu ngoại tiếp hình chóp đã cho.
Cách giải:
ABCD là hình thang cân có AB=CD=BC= a, AD = 2a
ABCD là 1 nửa của hình lục giác đều, có tâm O là trung điểm của AD.
Gọi I là trung điểm của SD.
OI// SA
Mà
I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD
I là tâm mặt cầu ngoại tiếp khối chóp S.BCD.
Bán kính mặt cầu ngoại tiếp khối chóp S.BCD là:
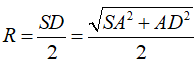
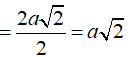
Thể tích khối cầu đó là:
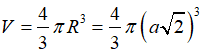
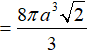
Câu 31:
Cho tam giác ABC có đường tròn nội tiếp (O;r) , cắt bỏ phần hình tròn và cho hình phẳng thu được quay quanh AO. Tính thể tích khối tròn xoay thu được theo r.
 Xem đáp án
Xem đáp án
Chọn A.

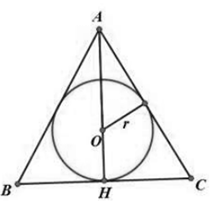

![]()
![]()


Câu 32:
Cho mặt cầu có diện tích bằng . Thể tích khối cầu là:
 Xem đáp án
Xem đáp án
Chọn C.
Phương pháp:
Hình cầu có bán kính R thì có diện tích là S = 4R2 và thể tích là:
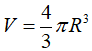
Cách giải:
Gọi bán kính hình cầu là R (R > 0)
Khi đó diện tích mặt cầu là:
S = 4R2 = 36a 2 ![]()
R = 3a
Thể tích khối cầu là :
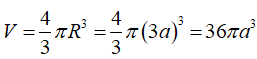
Câu 33:
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và tam giác SCD vuông cân tại S. Tính diện tích mặt cầu ngoại tiếp hình chóp.
 Xem đáp án
Xem đáp án
Chọn A.
Phương pháp:
+ Xác định chiều cao của hình chóp
+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD
Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.
+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.
+ Mặt cầu có bán kính R thì có diện tích là
Cách giải:
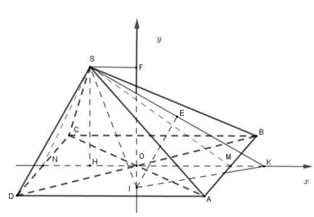
Gọi O là tâm hình vuông ABCD, gọi M , N lần lượt là trung điểm của AB; CD .
Kẻ SHMN tại H .
Ta có SNDC ; MN DC
DC( SMN )
DCSH
Mà SH MN
SH (ABCD).
Vì ABCD là hình vuông cạnh a nên:
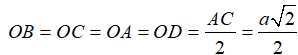
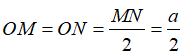
Vì tam giác SDC vuông cân tại S có cạnh huyền CD = a
SN=
Vì tam giác ABS đều cạnh a
SM =
Xét tam giác SNM có:
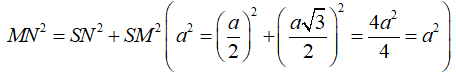
vuông tại S.
Suy ra:
![]()
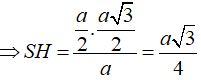
![]()
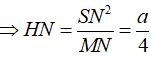
![]()
Nhận thấy O là tâm đường tròn ngoại tiếp hình vuông ABCD .
Kẻ tia Oy / /SH , khi đó tâm mặt cầu ngoại tiếp hình chóp S . ABCD nằm trên đường thẳng Oy.
Trên tia OM ta lấy K sao cho OK = OA =, khi đó K (O; OA)
Trong mặt phẳng (SMN ), lấy E là trung điểm SK , kẻ EI là đường trung trực của SK (I Oy).
Khi đó:
IK = IS = IA = IB = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S . ABCD và bán kính là R = IK.
Kẻ SF Oy
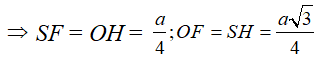
Gắn hệ trục Oxy với OM Ox; Oy / /SH
Đặt
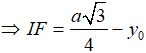
Xét tam giác vuông ISF có:
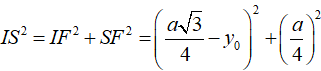
Xét tam giác vuông OIK có:
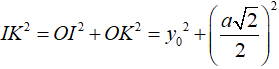
Vì ![]()
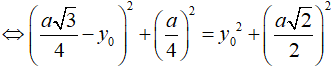
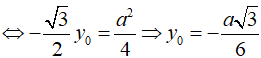
Suy ra bán kính mặt cầu:
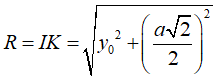
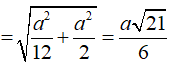
Diện tích mặt cầu ngoại tiếp hình chóp là:
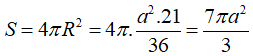
Câu 34:
Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là:
 Xem đáp án
Xem đáp án
Chọn C.



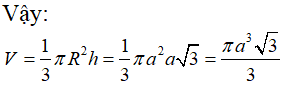
Câu 35:
Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a. Diện tích xung quanh hình nón đó bằng:
 Xem đáp án
Xem đáp án
Chọn A.
Diện tích xung quanh của hình nón có bán kính đáy R và đường sinh l là:
![]()
Cách giải:
Diện tích xung quanh của hình nón đó bằng:
![]()
Câu 36:
Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có AB=2a, BC= . Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại A () . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tính bán kính R của mặt cầu đó.
 Xem đáp án
Xem đáp án
Chọn A.
Phương pháp:
Chỉ ra ba đỉnh H, K, B cùng nhìn cạnh AC dưới một góc vuông. Từ đó suy ra bán kính mặt cầu đi qua 4 điểm A, H, B, K.
Cách giải:
Ta có:
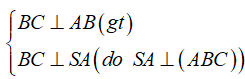
![]()
Mà:
![]()
![]()
Ta thấy:
![]()
Nên mặt cầu đi qua bốn đỉnh A; H; B; K nhận AC là đường kính nên bán kính:
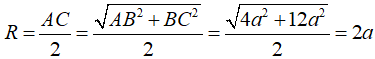
Câu 37:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
 Xem đáp án
Xem đáp án
Chọn C.
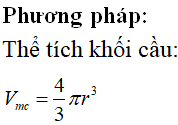


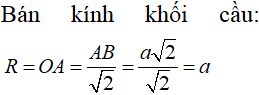
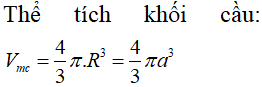
Câu 38:
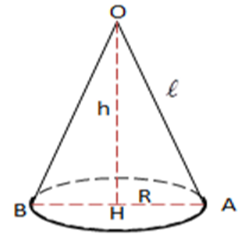
Cho khối nón có thiết diện qua trục là tam giác cân có một góc 1200 và cạnh bên bằng a . Tính thể tích khối nón.
 Xem đáp án
Xem đáp án
Chọn A.