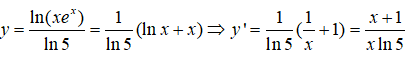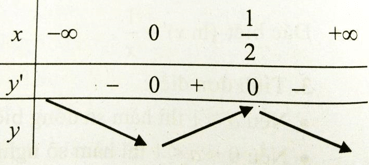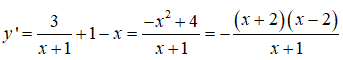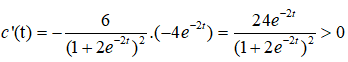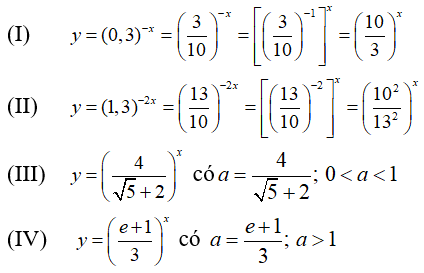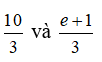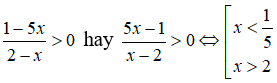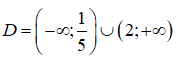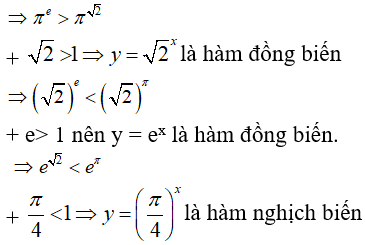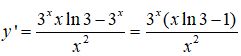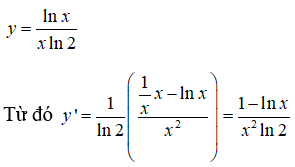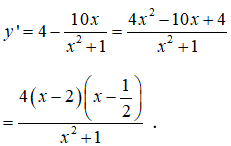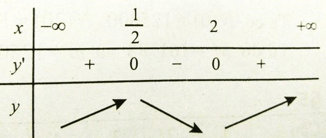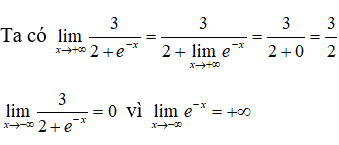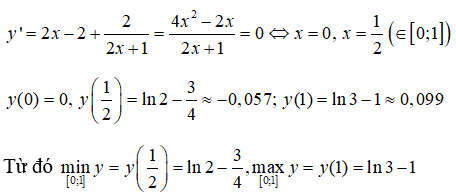32 câu trắc nghiệm: Hàm số mũ và hàm số lôgarit có đáp án
-
946 lượt thi
-
32 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
Tìm các khoảng đồng biến của hàm số
 Xem đáp án
Xem đáp án
Tập xác định R.
Ta có:
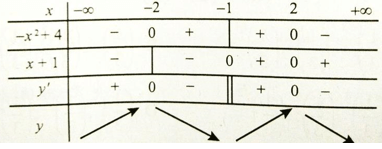
Bảng biến thiên
Khoảng đồng biến của hàm số là (0; 1/2) .
Chọn đáp án C
Câu 4:
Tìm các khoảng nghịch biến của hàm số
 Xem đáp án
Xem đáp án
Tập xác định : (-1; +∞)
Bảng biến thiên :
Kết hợp điều kiện, x > -1.
Từ đó, khoảng nghịch biến của hàm số là(2; +∞) .
Chọn đáp án B
Câu 7:
Số lượng cá thể của một mẻ cấy vi khuẩn sau t ngày kể từ lúc ban đầu được ước lượng bởi công thức Hãy tính số lượng cá thể của mẻ vi khuẩn ở hai thời điểm: ban đầu và sau 10 ngày. Làm tròn kết quả đến hàng trăm có kết quả là:
 Xem đáp án
Xem đáp án
Số lượng ban đầu: cá thể
Số lượng sau 10 ngày: cá thể
Chọn đáp án D.
Câu 8:
Dựa trên dữ liệu của WHO (Tổ chức Y tế thế giới), số người trên thế giới bị nhiễm HIV trong khoảng từ năm 1985 đến 2006 được ước lượng bằng công thức
trong đó N(t) tính bằng đơn vị triệu người, t tính bằng đơn vị năm và t = 0 ứng với đầu năm 1985. Theo công thức trên, có bao nhiêu số người trên thế giới bị nhiễm HIV ở thời điểm đầu năm 2005?
 Xem đáp án
Xem đáp án
Ta có 2005 – 1985 = 20 (năm). Vậy đầu năm 2005 ứng với t = 20. Số cần tìm
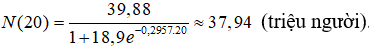
Chọn đáp án A.
Câu 9:
Biết rằng năm 2003 dân số Việt Nam là 80 902 000 người và tỉ lệ tăng dân số là 1,47%. Hỏi nếu vẫn giữ nguyên tỉ lệ tăng dân số hàng năm đó thì năm 2020 dân số Việt Nam sẽ là bao nhiêu (làm tròn kết quả đến hàng nghìn)?
 Xem đáp án
Xem đáp án
Công thức tính dân số theo dữ kiện đã cho là: ở đó thời gian t tính bằng năm và t = 0 ứng với đầu năm 2003.
Ta có 2020 – 2003 = 17.
Vậy năm 2020 ứng với t = 17
Dân số năm 2020 tính theo dữ kiện đã cho : ≈ 103870000 người.
Chọn đáp án C.
Câu 10:
Nồng độ c của một chất hóa học sau thời gian t xảy ra phản ứng tự xúc tác được xác định bằng công thức
Hãy chọn phát biểu đúng :
 Xem đáp án
Xem đáp án
với mọi t ≥ 0 nên c(t) tăng trên [0; +∞) , nghĩa là nồng độ c ngày càng tăng.
Chọn đáp án B.
Câu 11:
Cho các hàm số:
Trong các hàm số đã cho, hàm số nào đồng biến trên R ?
 Xem đáp án
Xem đáp án
Chọn B
Hàm số đồng biến khi a > 1.
Viết lại các hàm số về dạng hàm số mũ
Trong bốn cơ số ta thấy chỉ có hai cơ số lớn hơn 1 là
Do đó chỉ có hai hàm số (I) và (IV) là đồng biến trên R
Câu 12:
Cho các phát biểu sau đây về đồ thị của hàm số y = logax (0 < a ≠ 1):
(I) Cắt trục hoành
(II) Cắt trục tung
(III) Nhận trục tung làm tiệm cận đứng
(IV) Nhận trục hoành làm tiệm cận ngang
Trong những phát biểu trên, phát biểu nào đúng ?
 Xem đáp án
Xem đáp án
Đồ thị hàm số luôn cắt trục hoành tại điểm (1 ;0), luôn nằm bên phải trục tung (vậy không cắt trục tung), nhận trục tung làm tiệm cận đứng, không có tiệm cận ngang. Vậy chỉ có (I) và (III) đúng
Chọn D
Câu 13:
Tìm miền xác định của hàm số
 Xem đáp án
Xem đáp án
Điều kiện để hàm số xác định <=> < 0 <=> 0 < x < 1/2 .
Vậy miền xác định là D = (0; 1/2)
Chọn C
Câu 18:
Giá trị của một chiếc xe ô tô sau t năm kể từ khi mua được ước lượng bằng công thức (triệu đồng). Tính giá trị của chiếc xe này tại hai thời điểm : lúc mua và lúc đã sử dụng 5 năm (làm tròn kết quả đến hàng triệu)
 Xem đáp án
Xem đáp án
Chọn D
Giá trị xe lúc mua: G(0) = 600 triệu đồng
Giá trị xe sau khi mua 5 năm : G(5) ≈ 329 triệu đồng
Câu 22:
Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị hàm số với trục tung
Câu 23:
Tìm các khoảng đồng biến của hàm số
 Xem đáp án
Xem đáp án
Tập xác định : R
Bảng xét dấu
Khoảng đồng biến của hàm số là
Chọn C
Câu 24:
Cho hàm số Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
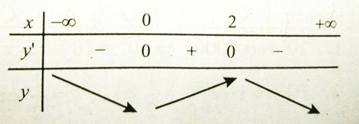
Bảng biến thiên
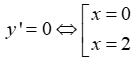
Từ bảng biến thiên ta thấy x = 0 là điểm cực tiểu, x = 2 là điểm cực đại của hàm số.
Chọn D
Câu 25:
Tìm các đường tiệm cận ngang của đồ thị hàm số
 Xem đáp án
Xem đáp án
Từ đó suy ra hàm số có hai tiệm cận ngang là y = 3/2 và y = 0
Vậy đồ thị hàm số đã cho có 2 tiệm cận ngang là: y = 3/2; y = 0
Chọn C
Câu 26:
Một quần thể vi khuẩn lúc đầu có 200 cá thể và cứ sau một ngày thì số lượng cá thể tăng lên gấp ba lần. Tìm công thức biểu thị số lượng cá thể (kí hiệu N) của quần thể này sau t ngày kể từ lúc ban đầu.
 Xem đáp án
Xem đáp án
Theo giả thiết, số lượng vi khuẩn sau 1, 2, 3,… ngày là 200.3 ; 200 .3.3 ; 200.3.3.3 ;… Từ đó ta thấy công thức đúng là
Chọn B
Câu 27:
Số lượng cá thể của một loài sinh vật bị suy giảm trong 10 năm theo cách : số lượng năm sau bằng 95% số lượng năm trước đó. Tại thời điểm chọn làm mốc thời gian loài này có 5000 cá thể. Công thức nào sau đây diễn tả số lượng cá thể (kí hiệu N) của loài theo thời gian t (tính bằng năm, 0 ≤ t ≤ 10 ) ?
 Xem đáp án
Xem đáp án
Tại thời điểm chọn làm mốc thời gian có 5000 cá thể.
Sau 1 năm số lượng cá thể còn lại là 5000. 95% = 0,95. 5000
Sau 2 năm số lượng cá thể còn lại là : (0,95. 5000). 0,95 = . 5000
...Sau t ( ) năm số lượng cá thể còn lại là :
Chọn B
Câu 28:
Một người gửi tiết kiệm vào ngân hàng số tiền 50 triệu đồng với hình thức lãi kép và lãi suất 6,8% một năm. Hỏi sau 3 năm trong tài khoản tiết kiệm của người đó có bao nhiêu tiền (làm tròn kết quả đến hàng nghìn) ?
 Xem đáp án
Xem đáp án
Số tiền trong tài khoản người đó sau n năm nếu người đó không rút tiền và lãi suất không thay đôỉ được tính theo công thức : (đồng)
Số tiền cần tính : (đồng)
Chọn B