15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Đường tiệm cận có đáp án (P1) (Vận dụng)

Câu 1:

Cho hàm số $y = \frac{2 m x + m}{x - 1} (C)$ . Với giá trị nào của m( $m \neq 0$ ) thì đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8?

A. m = 4

B. m = $\frac{1}{2}$

C. m = ±4

D. m = ±2

Xem đáp án

$y = \frac{2 m x + m}{x - 1} |\begin{matrix} x = 1 (T C D) \\ y = 2 m (T C N) \end{matrix}$

$S = 8 \Leftrightarrow |2 m| . |1| = 8 \Leftrightarrow |2 m| = 8 \Leftrightarrow 2 m = \pm 8 \Leftrightarrow m = \pm 4$

Đáp án cần chọn là: C

Câu 2:

Cho hàm số $y = \frac{x - 2}{x^{2} - 2 x + m}$ $y = \frac{x - 2}{x^{2} - 2 x + m} (C)$ . Tất cả các giá trị của m để (C ) có 3 đường tiệm cận là:

A. m < 1

B. m ≠ 0

C. m = −3

D. m < 1; m ≠ 0

Xem đáp án

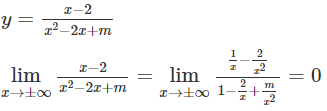
Suy ra y = 0 là tiệm cận ngang của đồ thị hàm số.

Để đồ thị hàm số có 3 đường tiệm cận $\Leftrightarrow$ đồ thị hàm số phải có hai đường tiệm cận đứng

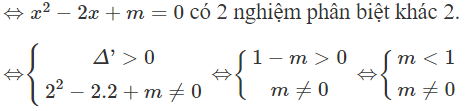
Đáp án cần chọn là: D

Câu 3:

Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số $y = \frac{x - 1}{x^{2} + 2 m x - m + 2}$ có đúng hai đường tiệm cận. Tổng tất cả các phần tử của tập S bằng:

A. -4

B. -2

C. -5

D. -1

Xem đáp án

Do đó, đồ thị hàm số đã cho luôn nhận đường thẳng y = 0 là tiệm cận ngang với mọi giá trị của m.

Đồ thị hàm số có đúng hai đường tiệm cận khi và chỉ khi nó có đúng 1 đường tiệm cận đứng.

Đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình $x^{2} + 2 m x - m + 2 = 0$ hoặc có nghiệm kép, hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 1 (1)

Phương trình $x^{2} + 2 m x - m + 2 = 0$ có $Δ' = m^{2} - (- m + 2) = m^{2} + m - 2$

$Δ' = m^{2} - (- m + 2) = m^{2} + m - 2$

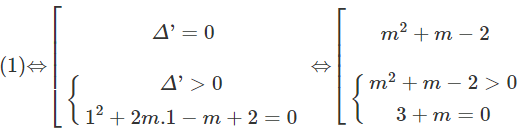
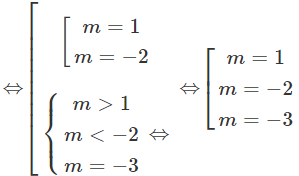
Do đó, tập các giá trị của tham số m thỏa mãn là: $S = \{1; - 2; - 3\}$

Vậy tổng tất cả các phần tử của tập hợp S bằng : 1 – 2 – 3 = - 4

Đáp án cần chọn là: A

Câu 4:

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc $[- 10; 10]$ để đồ thị hàm số $y = \frac{\sqrt{m x^{2} - 4}}{x - 1}$ có ba đường tiệm cận?

A. 7

B. 8

C. 10

D. 6

Xem đáp án

$\Rightarrow$ đồ thị hàm số có 2 đường tiệm cận ngang $y = \pm \sqrt{m}$ (m > 0)

Để đồ thị hàm số $y = \frac{\sqrt{m x^{2} - 4}}{x - 1}$ có 3 đường tiệm cận thì đồ thị hàm số phải có 1 đường tiệm cận đứng.

$\Rightarrow x = 1$ phải thỏa mãn điều kiện $m x^{2} \geq 4 \Leftrightarrow m \geq 4$

Do đó, $m \geq 4$ thì hàm số đã cho có 1 đường tiệm cận đứng và 2 đường tiệm cận ngang.

Mặt khác, $m \in [- 10; 10], m \in Z$ nên $m \in \{4; 5; 6; 7; 8; 9; 10\}$

Vậy có tất cả 7 giá trị nguyên của tham số m thỏa mãn bài toán.

Đáp án cần chọn là: A

Câu 5:

Cho hàm số $y = \frac{x - 3}{x^{3} - 3 m x^{2} + (2 m^{2} + 1) x - m}$ . Có bao nhiêu giá trị nguyên thuộc đoạn $[- 6; 6]$ của tham số m để đồ thị hàm số có bốn đường tiệm cận?

A. 12

B. 9

C. 8

D. 11

Xem đáp án

Nên y = 0 là tiệm cận ngang của đồ thị hàm số.

Vậy để đồ thị hàm số có 4 đường tiệm cận thì đồ thị hàm số phải có 3 đường tiệm cận đứng.

Hay phương trình $x^{3} - 3 m x^{2} + (2 m^{2} + 1) x - m = 0$ (1) có ba nghiệm phân biệt $x \neq 3$

$x \neq 3$

Câu 6:

Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số $y = \frac{\sqrt{x + 2}}{\sqrt{x^{2} - 6 x + 2 m}}$ $y = \frac{\sqrt{x + 2}}{\sqrt{x^{2} - 6 x + 2 m}}$ có hai đường tiệm cận đứng. Số phần tử của S là:

A. Vô số

B. 13

C. 12

D. 14

Xem đáp án

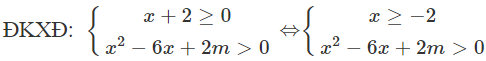
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình $x^{2} - 6 x + 2 m = 0$ có 2 nghiệm phân biệt thỏa mãn $x_{1} > x_{2} > - 2$

$x_{1} > x_{2} > - 2$

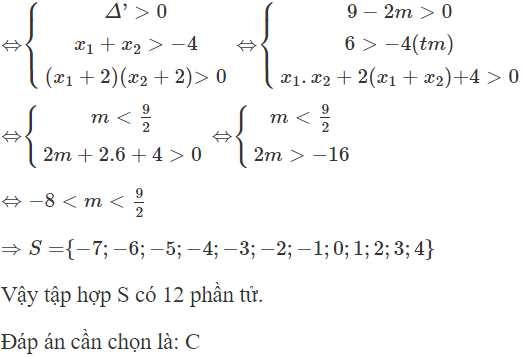
Câu 7:

Cho hàm số $y = \frac{2 x^{2} - 3 x + m}{x - m}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số m là:

A. m = 0

B. m = 0, m = 1

C. m = 1

D. Không tồn tại m

Xem đáp án

Với m = 0 ta có x = 0 là nghiệm của đa thức $2 x^{2} - 3 x$ trên tử $\Rightarrow y = 2 x - 3 (x \neq 0)$ không có tiệm cận đứng

Với m = 1 ta có x = 1 là nghiệm của đa thức $2 x^{2} - 3 x + 1$ trên tử $\Rightarrow y = 2 x - 1 (x \neq 1)$ không có tiệm cận đứng

Đáp án cần chọn là: B

Câu 8:

Cho hàm số $y = f (x)$ thỏa mãn $\lim_{x \to - \infty} f (x) = - 1$ và $\lim_{x \to + \infty} f (x) = m$ . Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số $y = \frac{1}{f (x) + 2}$ có duy nhất một tiệm cận ngang.

A. 1

B. 0

C. 2

D. Vô số

Xem đáp án

$\lim_{x \to - \infty} \frac{1}{f (x) + 2} = \frac{1}{\lim_{x \to - \infty} f (x) + \lim_{x \to - \infty} 2} = \frac{1}{- 1 + 2} \Rightarrow$ đồ thị hàm số $y = \frac{1}{f (x) + 2}$ có TCN y = 1

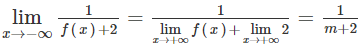
Để đồ thị hàm số $y = \frac{1}{f (x) + 2}$ có duy nhất một tiệm cận ngang thì $\underset{x \to + \infty}{l i m} \frac{1}{f (x) + 2}$ hoặc là không xác định hoặc là bằng 1.

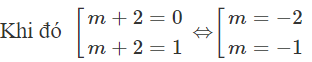
Vậy có 2 giá trị thực của m thỏa mãn yêu cầu bài toán.

Đáp án cần chọn là: C

Câu 9:

Cho hàm số $f (x) = \frac{a x + 1}{b x + c}$ (a,b,c ∈ R) có BBT như sau:

Trong các số a, b và c có bao nhiêu số dương?

A. 2

B. 3

C. 1

D. 0

Xem đáp án

Dựa vào BBT ta thấy đồ thị hàm số có TCĐ: $x = 2 \Rightarrow - \frac{c}{b} = 2 \Leftrightarrow c = - 2 b$

$x = 2 \Rightarrow - \frac{c}{b} = 2 \Leftrightarrow c = - 2 b$

Câu 10:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{1}{f (x) - 1}$ là:

A. 3

B. 6

C. 4

D. 5

Xem đáp án

Ta có: $\lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{1}{f (x) - 1} = \frac{1}{2 - 1} = 1$ , do đó đồ thị hàm số có TCN y = 1

$\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{1}{f (x) - 1} = 0$ , do đó đồ thị hàm số có TCN y = 0

Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{1}{f (x) - 1}$ là số nghệm của phương trình $f (x) = 1$

Dựa vào đồ thị hàm số ta thấy đường thẳng y = 1 cắt đồ thị hàm số $y = f (x)$ tại 4 điểm phân biệt nên phương trình $f (x) = 1$ có 4 nghiệm phân biệt. Suy ra đồ thị hàm số có 4 đường tiệm cận đứng.

Vậy đồ thị hàm số có tổng cộng 6 đường tiệm cận.

Đáp án cần chọn là: B

Câu 11:

Cho hàm số $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ bên

Hỏi đồ thị hàm số $g (x) = \frac{(x^{2} - 3 x + 2) \sqrt{x - 1}}{x [f^{2} (x) - f (x)]}$ có bao nhiêu tiệm cận đứng?

A. 4

B. 3

C. 5

D. 2

Xem đáp án

ĐKXĐ: $x \geq 1, f (x) \neq 0, f (x) \neq 1$

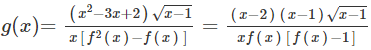
$g (x) = \frac{(x^{2} - 3 x + 2) \sqrt{x - 1}}{x [f^{2} (x) - f (x)]} = \frac{(x - 2) (x - 1) \sqrt{x - 1}}{x f (x) [f (x) - 1]}$ Nhận xét: $f (x) = a x^{3} + b x^{2} + c x + d$ là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:

+ $f (x) = 0$ có 2 nghiệm phân biệt $x = x_{1} (0 < x_{1} < 1)$ (ktm) (nghiệm đơn) và $x = 2$ (nghiệm kép)

+ $f (x) = 1$ có 3 nghiệm phân biệt x = 1 (nghiệm đơn), $x = x_{2} (1 < x_{2} < 2)$ (nghiệm đơn) và $x = x_{3} (x_{3} > 2)$ (nghiệm đơn)

Khi đó hàm số $y = g (x)$ được viết dưới dạng

Do đó, đồ thị hàm số g (x) có 3 đường tiệm cận đứng là: $x = x_{2}; x = 2; x = x_{3}$

Đáp án cần chọn là: B

Câu 12:

Cho hàm số $y = \frac{a x^{2} + 3 a x + 2 a + 1}{x + 2}$ . Chọn kết luận đúng:

A. Đồ thị hàm số luôn có tiệm cận xiên

B. Tiệm cận xiên của đồ thị hàm số luôn đi qua một điểm cố định a ≠ 0

C. Đồ thị hàm số luôn có 3 đường tiệm cận với ∀a

D. Đồ thị hàm số có tiệm cận ngang nếu a ≠ 0

Xem đáp án

+ Nếu a = 0 thì $y = \frac{1}{x + 2}$ , đồ thị hàm số này có tiệm cận đứng x = - 2 và tiệm cận ngang y = 0 nên A, C sai.

+ Nếu $a \neq 0$ thì $y = a x + a + \frac{1}{x + 2}$ nên $y = a x + a$ là đường tiệm cận xiên của đồ thị hàm số

Khi đó, $y = a x + a \Leftrightarrow a (x + 1) - y = 0$ luôn đi qua điểm $(- 1; 0)$ với mọi $a \neq 0$

Đáp án cần chọn là: B

Câu 13:

Cho đồ thị hàm số bậc ba $y = f (x)$ như hình vẽ. Hỏi đồ thị hàm số $y = \frac{(x^{2} + 4 x + 3) \sqrt{x^{2} + x}}{x [f^{2} (x) - 2 f (x)]}$ có bao nhiêu đường tiệm cận đứng?

A. 6

B. 3

C. 2

D. 4

Xem đáp án

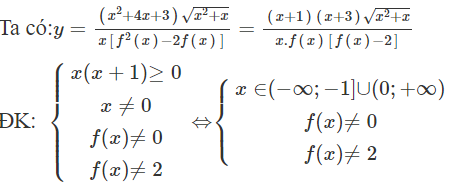
Dựa vào đồ thị hàm số ta thấy phương trình $f (x) = 0$ có nghiệm kép x = - 3 và 1 nghiệm $x = a \in (- 1; 0)$ , khi đó $f (x) = m {(x + 3)}^{2} (x - a) (m \neq 0)$

Xét phương trình $f (x) - 2 = 0 \Leftrightarrow f (x) = 2$ phương trình có 3 nghiệm phân biệt $x = - 1; x = b \in (- 3; - 1); x = c \in (- \infty; - 3)$

, khi đó $f (x) - 2 = n (x + 1) (x - b) (x - c)$

$f (x) - 2 = n (x + 1) (x - b) (x - c)$

Câu 14:

Số đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{\sqrt{x^{2} - 3}}$ là:

A. 4

B. 2

C. 1

D. 3

Xem đáp án

Câu 15:

Cho hàm số $y = \frac{\sqrt{x - 2}}{(x^{2} - 4) (2 x - 7)}$ . Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

A. 3

B. 2

C. 5

D. 4

Xem đáp án

$\lim_{x \to \frac{7}{2}} \frac{\sqrt{x - 2}}{(x^{2} - 4) (2 x - 7)} = \lim_{x \to \frac{7}{2}} \frac{1}{\sqrt{x - 2} (x + 2) (2 x - 7)} = \infty \Rightarrow x = \frac{7}{2}$ là đường TCĐ của đồ thị hàm số.

$\lim_{x \to 2} \frac{\sqrt{x - 2}}{(x^{2} - 4) (2 x - 7)} = \lim_{x \to 2} \frac{1}{\sqrt{x - 2} (x + 2) (2 x - 7)} = \infty \Rightarrow x = 2$ là đường TCĐ của đồ thị hàm số.

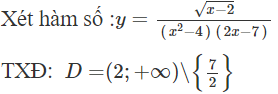
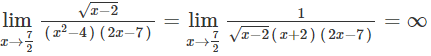
$\lim_{x \to + \infty} \frac{\sqrt{x - 2}}{(x^{2} - 4) (2 x - 7)} = \lim_{x \to + \infty} \frac{1}{\sqrt{x - 2} (x + 2) (2 x - 7)} = \infty \Rightarrow y = 0$ là đường TCĐ của đồ thị hàm số.

Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.

Đáp án cần chọn là: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Đường tiệm cận có đáp án (Vận dụng)

Trắc nghiệm Đường tiệm cận có đáp án (P1) (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương