Trắc nghiệm Phép chia số phức-Vận dụng (có đáp án)
-
694 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Cho số phức . Tìm phần thực của số phức .
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Nên phần thực cuả số phức w là: .
Câu 3:
Có bao nhiêu số phức z thỏa mãn và ?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Vậy có bốn số phức thỏa mãn bài toán là:
.
Câu 4:
Cho số phức z có tích phần thực và phần ảo bằng 625. Gọi a là phần thực của số phức . Giá trị nhỏ nhất của bằng.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 5:
Cho hai số phức khác 0 thỏa mãn là số thuần ảo và . Giá trị lớn nhất của bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta có: là số thuần ảo nên ta viết lại .
Khi đó
Xét
Phương trình có nghiệm
Vậy khi t = 1 hay .
Câu 6:
Cho các số phức z và w thỏa mãn . Tìm GTLN của .
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B.
Dễ dàng kiểm tra z = 0 không thỏa mãn .
Ta có:
Nhận xét:
Vậy MaxT=.
Câu 7:
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
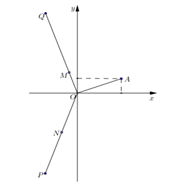
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Do điểm A là điểm biểu diễn của z nằm trong góc phần tư thứ nhất của mặt phẳng Oxy nên gọi .
Câu 8:
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
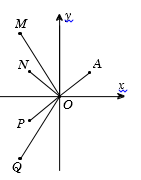
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Gọi . Từ giả thiết ta có
Ta có:
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (đều có hoành độ và tung độ âm).
Đồng thời
Suy ra, điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA.
Quan sát hình vẽ ta thấy có điểm P thỏa mãn.
Câu 9:
Cho số phức z thay đổi, luôn có . Khi đó tập hợp điểm biểu diễn số phức là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
.
Hãy tập hợp điểm biểu diễn số phức là đường tròn .
