21 câu hỏi trắc nghiệm thuộc 225 Bài tập Số phức ôn thi Đại học có lời giải (P1)

Câu 1:

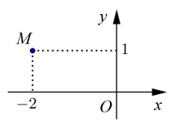
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên ?

A. $z_{1}$ = 1 - 2i

B. $z_{2}$ = 1 + 2i

C. $z_{3}$ = -2 + 2i

D. $z_{4}$ = -2 + i

Xem đáp án

Đáp án C

Số phức z = a+bi có điểm biểu diễn là M(a;b)

$\Rightarrow$ Điểm M(-2;1) biểu diễn số phức z = -2+i

Câu 2:

Kí hiệu z₁ ; z₂ là hai nghiệm phức của phương trình $3 z^{2} - z + 1 = 0$ .Tính P = $|z_{1}| + |z_{2}|$

$A . P = \frac{\sqrt{14}}{3}$

$B . P = \frac{2}{3}$

$C . P = \frac{\sqrt{3}}{3}$

$D . P = \frac{2 \sqrt{3}}{3}$

Xem đáp án

Đáp án D

$z_{1}, z_{2}$ là nghiệm phức của phương trình $3 z^{2} - z + 1 = 0$

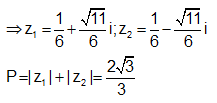
Câu 3:

Số phức nào dưới đây là số thuần ảo ?

A. z = -2 + 3i

B. z = 3i

C. z = -2

D. z = $\sqrt{3}$ + i

Xem đáp án

Đáp án B

Số ảo z = a + bi gọi là số thuần ảo nếu a = 0 và b $\neq$ 0

Do đó z = 3i là số thuần ảo

Câu 4:

Cho hai số phức $z_{1}$ = 5 - 7i và $z_{2}$ = 2 + 3i. Tìm số phức z = $z_{1}$ + $z_{2}$

A. z = 7 - 4i

B. z = 2 + 5i

C. z = -2 + 5i

D. z = 3 - 10i

Xem đáp án

Đáp án A

z = $z_{1}$ + $z_{2}$ = 5-7i+2+3i = 7 - 4i

Câu 5:

Phương trình nào dưới đây nhận hai số phức $1 + \sqrt{2} i$ và $1 - \sqrt{2} i$ là nghiệm ?

$A . z^{2} + 2 z + 3 = 0$

$B . z^{2} - 2 z - 3 = 0$

$C . z^{2} - 2 z + 3 = 0$

$D . z^{2} + 2 z - 3 = 0$

Xem đáp án

Đáp án C

Cách 1: bấm máy tính giải các phương trình ở đáp án

Cách 2: Ta có:

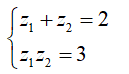
=> Áp dụng Vi-et ta được phương trình là:

$z^{2} - 2 z + 3 = 0$

Câu 6:

Cho số phức z = 1 - 2i . Điểm nào dưới đây là điểm biểu diễn của số phức w = iz trên mặt phẳng tọa độ ?

A. Q(1;2)

B. N(2;1)

C. M(1;-2)

D. P(-2;1)

Xem đáp án

Đáp án B

w = iz = i(1-2i) = 2 + i

Vậy điểm biểu diễn w có tọa độ là: (2;1)

Câu 7:

Cho số phức z = a + bi, (a, b $\in ℝ$ ) thỏa mãn z + 1 + 3i - |z|i = 0. Tính S = a + 3b

A. S = $\frac{7}{3}$

B. S = -5

C. S = 5

D. S = - $\frac{7}{3}$

Xem đáp án

Đáp án B

Ta có:

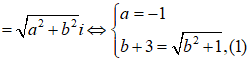
Với b $⩾$ -3 thì (1) tương đương với: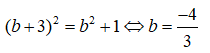

Vậy a + 3b = -5

Câu 8:

Có bao nhiêu số phức z thỏa mãn |z-3i| = 5 và $\frac{z}{z - 4}$ là số thuần ảo ?

A. 0

B. Vô số

C. 1

D. 2

Xem đáp án

Đáp án C

Đặt z = x + yi (x,y $\in ℝ$ )

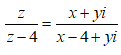
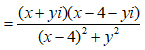
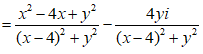
$\frac{z}{z - 4}$ là số thuần ảo nên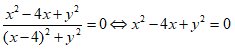

Ta có hệ: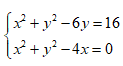

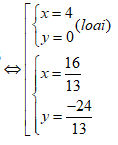
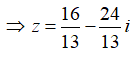
Vậy chỉ có 1 số phức z thỏa mãn

Câu 9:

Cho hai số phức $z_{1}$ = 4 - 3i và $z_{2}$ = 7 + 3i. Tìm số phức z = z₁ - z₂

A. z = 11

B. z = 3 + 6i

C. z = -1 - 10i

D. z = -3 - 6i

Xem đáp án

Chọn đáp án A

z = $z_{1}$ - $z_{2}$ = 4-3i-7-3i = -3-6i

Câu 10:

Kí hiệu $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $3 z^{2}$ - z + 1 = 0. Tính P = | $z_{1}$ |+| $z_{2}$ |

A. P = $\frac{\sqrt{3}}{3}$

B. P = $\frac{2 \sqrt{3}}{3}$

C. P = $\frac{2}{3}$

D. P = $\frac{\sqrt{14}}{3}$

Xem đáp án

Chọn đáp án B

Câu 11:

Cho hai số phức $z_{1}$ = 1-3i và $z_{2}$ = -2-5i . Tìm phần ảo b của số phức z = $z_{1}$ - $z_{2}$

A. b = -2

B. b = 2

C. b = 3

D. b = -3

Xem đáp án

Đáp án B

Câu 12:

Cho số phức z = 2 - 3i . Tìm phần thực a của z

A. a = 2

B. a = 3

C. a = -3

D. a = -2

Xem đáp án

Đáp án A

Phần thực a = 2

Câu 13:

Tìm tất cả các số thực x, y sao cho $x^{2}$ - 1 + yi = -1 + 2i

$A . x = - \sqrt{2}, y = 2$

$B . x = \sqrt{2}, y = 2$

$C . x = 0, y = 2$

$D . x = \sqrt{2}, y = - 2$

Xem đáp án

Đáp án C

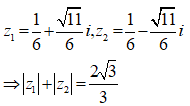
Câu 14:

Kí hiệu $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2}$ - z + 6 = 0 . Tính P = $\frac{1}{z_{1}} + \frac{1}{z_{2}}$

A. P = $\frac{1}{6}$

B. P = $\frac{1}{12}$

C. P = - $\frac{1}{6}$

D. P = 6

Xem đáp án

Đáp án A

Theo Vi-et:

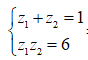
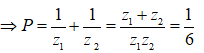
Câu 15:

Cho số phức z thỏa mãn |z + 3| = 5 và |z - 2i| = |z - 2 - 2i|. Tính |z|

A. |z| = 17

B. |z| = $\sqrt{17}$

C. |z| = $\sqrt{10}$

D. |z| = 10

Xem đáp án

Đáp án C

Giả sử z = a + bi(a, b $\in ℝ$ )

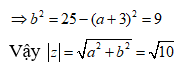
Câu 16:

Có bao nhiêu số phức z thỏa mãn |z + 3i| = $\sqrt{13}$ và $\frac{z}{z + 2}$ là số thuần ảo ?

A. vô số

B. 2

C. 0

D. 1

Xem đáp án

Đáp án D

Đặt

Ta có: 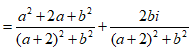là số thuần ảo thì

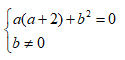
Khi đó ta có hệ:

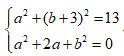
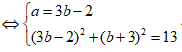
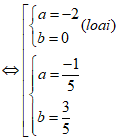
Vậy chỉ có 1 số phức z thỏa mãn.

Câu 17:

Tìm số phức z thỏa mãn z+2-3i= 3-2i

A. z=1-5i

B. z=5-5i

C. z=1-i

D. z=1+i

Xem đáp án

Đáp án D

Đặt z=a+bi thay vào ta có

a+bi+2-3i=3-2i

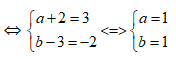
=> z=1+i

Câu 18:

Cho số phức z=2+i . Tính |z|

A. |z| = 5

B. |z| = 2

C. |z| = $\sqrt{5}$

D. |z| = 3

Xem đáp án

Đáp án C

Câu 19:

Kí hiệu $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2}$ + 4 = 0. Gọi M,N lần lượt là các điểm biểu diễn của $z_{1}, z_{2}$ trên mặt phẳng tọa độ.Tính T = OM+ON với O là gốc tọa độ.

A. T = 2 $\sqrt{2}$

B. T = 2

C. T = 8

D. T = 4

Xem đáp án

Đáp án D

pt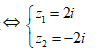

Suy ra M(0,2) N(0,-2) suy ra OM=ON=2 suy ra T= OM+ON=4

Câu 20:

Cho số phức $z_{1}$ = 1 - 2i, $z_{2}$ = -3 + i. Tìm điểm biểu diễn số phức z = $z_{1}$ + $z_{2}$ trên mặt phẳng tọa độ.

A. M(2;-5)

B. N(4;-3)

C. P(-2;-1)

D. Q(-1;7)

Xem đáp án

Đáp án C

suy ra N(-2;-1)

Câu 21:

Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i

A. w=-4+8i

B. w=1+3i

C. w= -1+7i

D. w=-3+8i

Xem đáp án

Đáp án A

Đặt z= a+bi

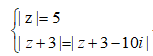
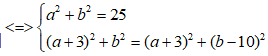
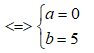
=> z = 5i

=> w=z-4+3i = 5i-4+3i= -4+8i

CHỌN BỘ SÁCH BẠN MUỐN XEM

225 Bài tập Số phức ôn thi Đại học có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải (P1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm