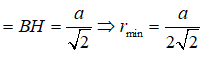32 câu trắc nghiệm: Mặt cầu (có đáp án)
-
862 lượt thi
-
32 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho mặt cầu tâm O bán kính R và điểm A bất kì trong không gian. Điểm A không nằm ngoài mặt cầu khi và chỉ khi:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 2:
Cho hình chóp S.ABC có đáy là tam giác vuông cân đỉnh B và BC = a, SA ⊥ (ABC), SA = 2a. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có: SA = 2a = r; AB = a < r và
Câu 3:
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
 Xem đáp án
Xem đáp án
Đáp án D
Từ vị trí tương đối của một mặt phẳng với mặt cầu ta có đáp án đúng là D.
Câu 4:
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
 Xem đáp án
Xem đáp án
Đáp án A
Từ vị trí tương đối của một đường thẳng và mặt cầu ta có đường thẳng d có điểm chung với mặt cầu (S) khi và chỉ khi đường thẳng d tiếp xúc hoặc cắt mặt cầu (S).
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) theo a là:
 Xem đáp án
Xem đáp án
Đáp án D
Ta có mặt cầu S(A;r) tiếp xúc với mặt phẳng (SBC) khi và chỉ khi r = d(A; (SBC)).
Hạ AH ⊥ SB tại H. Do BC ⊥ AB và BC ⊥ SA nên BC ⊥ (SAB) , suy ra BC ⊥ AH.
Mặt khác AH ⊥ SB nên AH ⊥ (SBC) hay d(A; (SBC)) = AH Xét tam giác vuông SAB ta có:
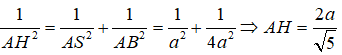
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2AD = 2a. SA vuông góc với đáy, góc giữa cạnh bên SB và đáy là 45o. Bán kính mặt cầu tâm A cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a là:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có mặt cầu S(A;r) cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a khi và chỉ khi
![]()
![]()
Hạ AK ⊥ BD tại K, hạ AH ⊥ SK tại H.
Do BD ⊥ AK và BD ⊥ SA nên BD ⊥ (SAK), suy ra BD ⊥ AH.
Mặt khác AH ⊥ SK nên ta có AH ⊥ (SBDB) hay d(A; (SBD)) = AH.
Xét tam giác vuông SAK và tam giác vuông ABD ta có:
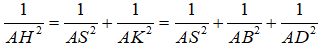
Khi đó ta có:
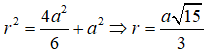
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = 2a. Bán kính mặt cầu tâm A tiếp xúc với SC theo a là:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có mặt cầu S(A ;r) tiếp xúc với đường thẳng SC khi và chỉ khi ta có r = d(A; SC).
Xét tam giác vuông ABC ta có AC = a. Hạ AH ⊥ SC tại H. Xét tam giác vuông SAC ta có:
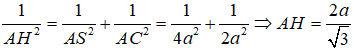
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là:
 Xem đáp án
Xem đáp án
Đáp án C
Do (SAB) ⊥ (ABCD) và (SAD) ⊥ (ABCD) ta có SA ⊥ (ABCD). Theo định lí ba đường vuông góc ta có BC ⊥ SB.
Hạ BH ⊥ SC tại H. Xét tam giác vuông SBC ta có:
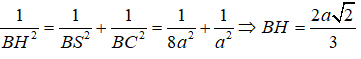
Ta có mặt cầu S(B;r) cắt đường thẳng SC theo một dây cung có độ dài 2a khi và chỉ khi ta có
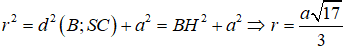
Câu 9:
Cho hai quả cầu cùng bán kính là 5cm. Để đựng hai quả cầu Nam phải làm một hình hộp chữ nhật từ bìa carton. Hỏi trong các đáp án dưới đây, Nam cần ít nhất bao nhiêu xen-ti-mét vuông bìa carton để làm được chiếc hộp đó?
 Xem đáp án
Xem đáp án
Đáp án B
Hình hộp chữ nhật đựng được hai quả cầu bán kính 5cm thì độ dài các cạnh ít nhất là 10cm, 10cm, 20cm. Khi đó ta có: Stp = 2 x 102 + 4 x 10 x 20 = 1000(cm2).
Câu 10:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án D
Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp đó có đáy là một đa giác nội tiếp được đường tròn nên mệnh đề A và B đúng. Hình chóp có các cạnh bên bằng nhau có hình chiếu vuông góc của đỉnh lên mặt đáy là tâm đường tròn ngoại tiếp đáy nên hình chóp đó có đáy nội tiếp được đường tròn và do đó đáp án C đúng.
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
 Xem đáp án
Xem đáp án
Đáp án C
Theo định lí ba đường vuông góc ta có tam giác SBC, SDC lần lượt vuông tại B, D. Gọi I là trung điểm của SC. Từ các tam giác SAC, SBC, SDC vuông ta có:
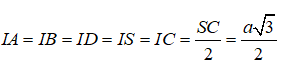
Vậy I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD và bán kính mặt cầu là
Câu 13:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
![]()
![]()
Ta nhận thấy tâm I của mặt cầu ngoại tiếp hình lập phương chính là tâm của hình lập phương đó. Do đó I chính là trung điểm của AC’ và mặt cầu ngoại tiếp hình lập phương có bán kính là
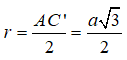
Câu 15:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S,ABC, biết các cạnh đáy có độ dài bằng a , cạnh bên SA = .
 Xem đáp án
Xem đáp án
Đáp án D


Câu 16:
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
 Xem đáp án
Xem đáp án
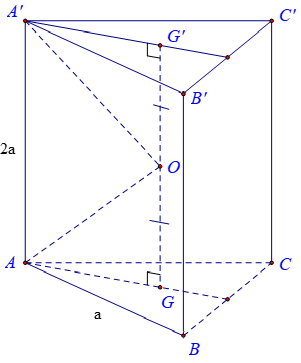
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có:
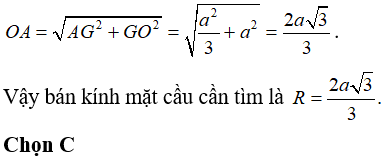
Câu 17:
Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng:
 Xem đáp án
Xem đáp án
Đáp án C
Gọi S(I; r) là mặt cầu đi qua A và tiếp xúc với a.
Ta có diện tích của mặt cầu là: S = 4π nên S đạt giá trị nhỏ nhất khi và chỉ khi r đạt giá trị nhỏ nhất.
Gọi tiếp điểm của đường thẳng a và mặt cầu là H và hình chiếu vuông góc hạ từ A lên đường thẳng A là A’. Khi đó ta có:
2r = IA + IH ≥ AH ≥ AA' => r ≥ = 2(cm)
Vậy r đạt giá trị nhỏ nhất bằng 2cm khi I là trung điểm của AA’.
Khi đó mặt cầu (S) có diện tích nhỏ nhất là S = 4π = 16π(c).
Câu 18:
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu:
 Xem đáp án
Xem đáp án
Đáp án C
Từ vị trí tương đối của một mặt phẳng và mặt cầu ta có mặt phẳng (P) có điểm chung với mặt cầu (S) khi và chỉ khi mặt phẳng (P) tiếp xúc hoặc cắt mặt cầu (S).
Câu 19:
Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng:
 Xem đáp án
Xem đáp án
Đáp án C
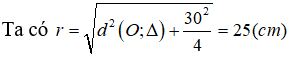
Câu 20:
Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
 Xem đáp án
Xem đáp án
Đáp án C
Gọi O là tâm của tam giác đều ABC.
Nên:
Ta có:
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, DSAB là tam giác đều. Bán kính mặt cầu tâm A cắt SB theo một dây có độ dài a là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi S(A;r) là mặt cầu tâm A cắt đường thẳng SB theo một dây có độ dài a, khi đó ta có:
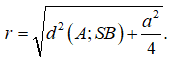
Gọi H là trung điểm của SB. Do tam giác SAB đều nên AH ⊥ SB hay AH là khoảng cách từ A đến SB. Xét tam giác đều SAB ta có:
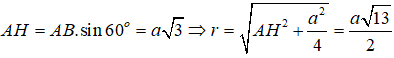
Câu 22:
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
 Xem đáp án
Xem đáp án
Đáp án C
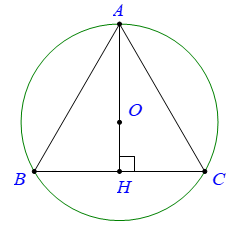

Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là
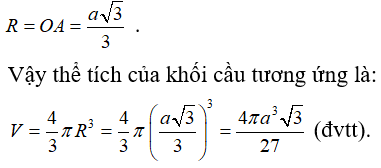
Câu 23:
Cho tam giác ABC vuông tại A có BC = 2a và = 30°. Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S1 là diện tích toàn phần của hình nón đó và là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số là:
 Xem đáp án
Xem đáp án
Đáp án A

Câu 25:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
 Xem đáp án
Xem đáp án
Đáp án D
Theo định lí ba đường vuông góc ta có hai tam giác SBC và SDC lần lượt vuông góc tại B, D. Gọi I là trung điểm của SC thì ta có: IA = IB = ID = = IS = IC nên I là tâm mặt cầu ngoại tiếp hình chóp. Bán kính mặt cầu ngoại tiếp hình chóp là
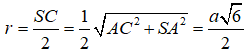
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
 Xem đáp án
Xem đáp án
Đáp án C
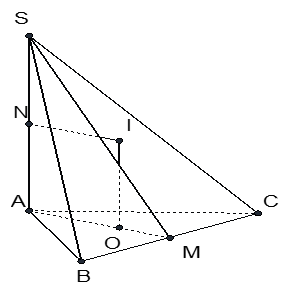

Câu 27:
Cho hình chóp tứ giác đều S.ABCD có góc giữa SA và đáy là 60o, SA = 2a. Bán kính mặt cầu ngoại tiếp hình chóp là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi O là tâm của hình vuông ABCD. Khi đó SO ⊥ (ABCD) và SO là trục của đường tròn ngoại tiếp hình vuông ABCD. Từ giả thiết ta có:
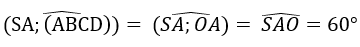
Trong mặt phẳng (SAO), đường trung trực của SA cắt SO tại I. Khi đó I cách đều các đỉnh của hình chóp nên I là tâm mặt cầu ngoại tiếp hình chóp. Gọi M là trung điểm của SA, khi đó ta có:
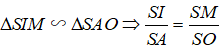
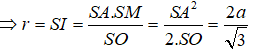
Câu 28:
Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)

Câu 29:
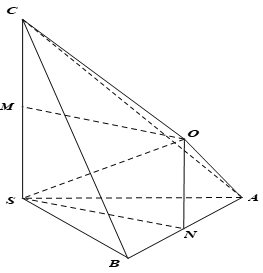
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = a và góc giữa A’B và mặt phẳng (ABC) là 60o. Bán kính của mặt cầu ngoại tiếp lăng trụ là:
 Xem đáp án
Xem đáp án
Đáp án B
Trong tam giác vuông ABC ta có
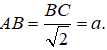
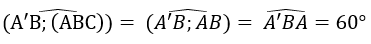
AA' = AB.tan60o = a
Gọi I là tâm của hình chữ nhật BCC’B’ và M là trung điểm của BC. Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC và do đó IM là trục của đường tròn ngoại tiếp đáy ABC và I cách đều B, B’ nên I là tâm của mặt cầu ngoại tiếp lăng trụ. Khi đó ta có:
![]()
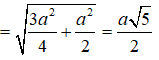
Câu 30:
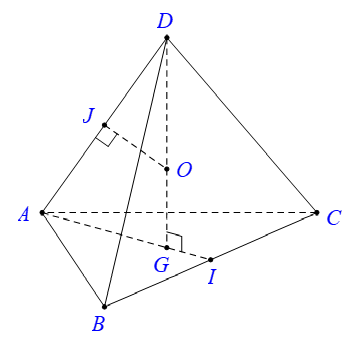
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD theo a.
 Xem đáp án
Xem đáp án
Đáp án D

Gọi H là trung điểm của AB, do tam giác SAB đều nên SH ⊥ AB mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD)
Gọi O là tâm của hình vuông ABCD, d là đường thẳng qua O và song song SH thì d ⊥ (ABCD) hay d là trục đường tròn ngoại tiếp hình vuông ABCD
Trong mặt phẳng (SAB) từ G kẻ đường thẳng vuông góc với (SAB) cắt d tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R = IS.
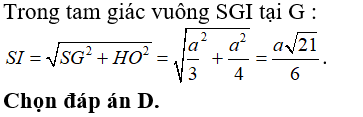
Câu 31:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
 Xem đáp án
Xem đáp án
Đáp án A

Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông.
Gọi M là trung điểm của ABCD .
Trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O
Thì OS = OA = OC = OD
Nên O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
Bán kính mặt cầu là R = SO.
Ta có:
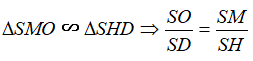
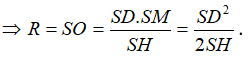
![]()
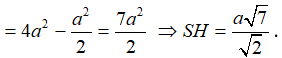
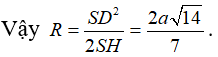
Câu 32:
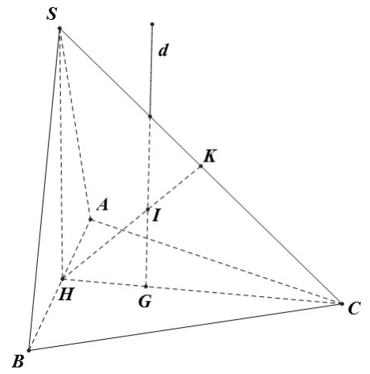
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a, SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là:
 Xem đáp án
Xem đáp án
Đáp án C
Mặt cầu S(I,r) tiếp xúc với AB, SC lần lượt tại T, K. Khi đó ta có:
2r = IT + IK ≥ d(AB; SC) => r ≥
Dựng hình bình hành ABDC, khi đó ta có ABDC là hình vuông cạnh a. Hạ BH vuông góc với SD tại H. Khi đó ta có BH ⊥ (SCD).
Suy ra: d(SC; AB) = d(AB, (SCD)) = d(B; (SCD))