Trắc nghiệm Cực trị của hàm số có đáp án
Trắc nghiệm Cực trị của hàm số có đáp án (P1)
-
1356 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số f (x) có đạo hàm liên tục trên R. Đồ thị hàm số y=f'(x) như hình bên. Hàm số y=f(x2+4x)−x2−4x có bao nhiêu điểm cực trị thuộc khoảng (−5;1)
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
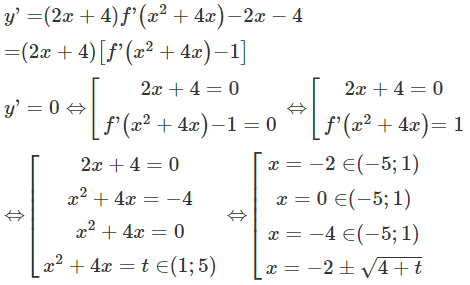
Xét x1=−2−√4+t, với 1<t<5⇒−5<−2−√4+t<−2−√5<1⇒−5<x1<1
Xét x2=−2+√4+t, với 1<t<5⇒−5<−2+√4+t<−2+√5<1⇒−5<x2<1
Do đó phương trình y’ = 0 có 5 nghiệm phân biệt thuộc (-5; 1) và các nghiệm này đều là nghiệm bội lẻ nên đạo hàm y’ đổi dấu qua chúng.
Vậy hàm số có 5 điểm cực trị trong khoảng (-5; 1)
Câu 2:
Cho hai hàm số bậc bốn y=f(x) và y=g(x) có các đồ thị như hình dưới đây (2 đồ thị có đúng 3 điểm chung)
Số điểm cực trị của hàm số h(x)=f2(x)+g2
(x)−2f(x).g(x) là:
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
h(x) =[ f(x) − g(x) ]2
⇒h'(x) =2[ f(x) − g(x) ] . [ f(x) − g(x) ]'=2 [ f(x) − g(x) ].[ f'(x) − g'(x)]
Cho h'(x) =0⇔[f(x) − g(x) =0 (1)f'(x) − g'(x) =0 (2)
Từ đồ thị hàm số ta thấy phương trình (1) có 3 nghiệm phân biệt ⎡⎢⎣x=−1x=x1x=3∈(−1;3) và đa thức f(x)−g(x
Câu 3: Cho hàm số y=f(x) có đạo hàm f'(x) có đồ thị như hình dưới đây Số điểm cực trị của hàm số g(x)=8f(x3−3x+3)−(2x6−12x4+16x3+18x2−48x+1) là: Đáp án B Đặt t=x3−3x+3, phương trình (*) trở thành f'(t)=12(t+1), do đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f'(t) và y=12(t+1) Dựa vào đồ thị hàm số ta thấy (*) ⇔ ⎡⎢⎣t=−1t=1t=5t=t0∈(1;5) + Với t=−1⇒x3−3x+3=−1, phương trình này có 1 nghiệm không nguyên + Với t=1⇒x3−3x+3=1⇔[x=1x=−2, trong đó x = 1 là nghiệm bội 2. + Với t=5⇒x3−3x+3=5⇔
Câu 4: Cho hàm số y=f(x)=ax4+bx2+c biết a>0,c>2017 và a+b+c<2017. Số điểm cực trị của hàm số y=|f(x)−2017| là: Đáp án B Hàm số y=f(x)=ax4+bx2+c xác định và liên tục trên D = R Ta có: f(0)=c>2017>0 f(−1)=f(1)=a+b+c<2017 Do đó [f(−1)−2017].[f(0)−2017]<0 và [f(1)−2017].[f(0)−2017]<0 Mặt khác limx→±∞f(x)=+∞ nên ∃α<0,β>0 sao cho f(α)>2017,f(β)>2017 [f(α)−2017].[f(−1)−2017]
Câu 5: Cho hàm số f (x) có đạo hàm f'(x)=x(x−1)(x+2)3 Đáp án A Ta có: f'(x)=0⇔x(x−1)(x+2)3=0⇔⎡⎢⎣x=0x=1x=−2 và các nghiệm này đều là nghiệm bội bậc lẻ nên hàm số đã cho có ba điểm cực trị. Câu 6: Cho hàm số f (x) có đạo hàm f'(x)=(x2+x)(x−2)2(2x−4),∀x∈R. Số điểm cực trị của f (x) là: Đáp án C Ta có f'(x)= 0 Ta thấy phương trình f'(x)=0 có ba nghiệm phân biệt và các nghiệm này đều là nghiệm bội lẻ nên hàm số y=f(x) có 3 điểm cực trị. Câu 7: Cho hàm số f(x)=x2(x−1)e3x có một nguyên hàm là hàm số F(x). Số cực trị của hàm số F(x) là: Đáp án A Vì hàm số f(x)=x2(x−1)e3x có một nguyên hàm là hàm số F(x) nên F'(x)=f(x)=x2(x−1)e3x Xét F'(x)=0⇔x2(x−1)e3x=0⇔[x=0x=1 Bảng biến thiên của hàm F(x): Vậy hàm số có 1 điểm cực trị. Câu 8: Đồ thị hàm số y=x3−3x+2 có 2 điểm cực trị A, B. Diện tích tam giác OAB với O (0; 0) là gốc tọa độ bằng: Đáp án A y=x3 Tọa độ 2 điểm cực trị: A (1; 0); B (-1; 4) Khi đó: SΔOAB=12.OA.d(B,OA)=12|xA|.|yB|=12|1|.|4|=2 Câu 9: Cho hàm số y=x4−2x2+2. Diện tích S của tam giác có 3 đỉnh là 3 điểm cực trị của đồ thị hàm số đã cho có giá trị là: Đáp án C y=x4−2x2+2(C) ⇒y'=4x3−4xy'=0⇔[x=0x=±1 Tọa độ các điểm cực trị của (C) là: A(0;2),B(−1;1),C(1;1) Diện tích tam giác ABC: SABC=12 AH.BC=12.(2−1).(1−(−1))=1 Câu 10: Hàm số y=x3−3x2+4 đạt cực tiểu tại Đáp án B TXĐ: D = R Ta có: y'=3x2−6x ⇒y'=0⇔x=0 hoặc x = 2 Ta có bảng biến thiên: Từ bảng dễ thấy hàm số đạt giá trị cực tiểu y = 0 tại x = 2 Câu 11: Hàm số y=x3−12x+3 đạt cực đại tại điểm: Đáp án A TXĐ: D = R Ta có: y'=3x2−12,y''=6x Xét hệ {y'=0y''<0⇔ {3x2−12=06x<0⇔ {x=±2x<0⇔x=−2 Vậy hàm số đạt cực đại tại điểm x = - 2. Câu 12: Điểm cực tiểu của đồ thị hàm số y=x3−3x+5 là điểm: Đáp án D Có y'=3x2−3=0⇔x=±1 Vì hệ số của x3 là dương nên đồ thị hàm số có điểm cực tiểu (1; 3) Câu 13: Cho hàm số , chọn kết luận đúng: Đáp án A BBT Từ BBT ta thấy đồ thị hàm số có điểm cực đại là (0; 3) và điểm cực tiểu là (-4; 11) Câu 14: Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây. Hàm số đạt cực tiểu tại điểm nào trong các điểm sau? Đáp án D Hàm số đạt cực tiểu tại điểm x = 2 Câu 15: Cho hàm số y=f(x) có bảng biến thiên như sau: Giá trị cực đại của hàm số đã cho bằng: Đáp án D Quan sát bảng biến thiên ta thấy hàm số đạt cực đại tại điểm x = 2 và giá trị cực đại của hàm số là 5 Câu 16: Cho hàm số f (x) có bảng biến thiên như sau: Giá trị cực đại của hàm số đã cho bằng: Đáp án B Dựa vào BBT ta thấy hàm số có điểm cực đại là x = 0 và giá trị cực đại là ycd=y(0)=2 Câu 17: Cho hàm số y=f(x) có bảng biến thiên như sau: Hàm số đạt cực đại tại điểm Đáp án D Quan sát bảng biến thiên ta thấy hàm số đạt tiểu tại điểm x = 0 và đạt cực đại tại x = 2 Câu 18: Cho hàm số y=f(x) có bảng biến thiên như sau: Hàm số y=f(x) đạt cực đại tại điểm Đáp án A Dựa vào BBT ta thấy hàm số y=f(x) đạt cực đại tại điểm x = - 2 Câu 19: Cho hàm số y=f(x) có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng? Đáp án D Từ BBT ta thấy, đạo hàm không đổi dấu trên (−∞;+∞) nên hàm số không có cực trị. Câu 20: Cho hàm số y = f(x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng? Đáp án B Dựa vào đồ thị hàm số ta thấy hàm số có 2 điểm cực trị suy ra loại đáp án D. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại tại x = 0. Suy ra đáp án B đúng Câu 21: Cho hàm số y = f(x) có bảng biến thiên như hình bên dưới, chọn khẳng định sai: Đáp án C Từ BBT ta thấy: Đạo hàm đổi dấu từ dương sang âm qua điểm x = 2 nên x = 2 là điểm cực đại của hàm số, y = 3 là giá trị cực đại của hàm số và (2; 3) là điểm cực đại của đồ thị hàm số. Ngoài ra, đạo hàm không đổi dấu qua điểm x = - 2 nên x = - 2 không là điểm cực trị của hàm số. Câu 22: Cho hàm số y = f(x) liên tục tại x0 và có bảng biến thiên sau: Mệnh đề nào sau đây là đúng? Đáp án A Hàm số có một điểm cực đại là x1, một điểm cực tiểu là x0 Câu 23: Cho hàm số y = f(x) có bảng biến thiên như sau: Hàm số đạt cực đại tại điểm: Đáp án A Dựa vào đồ thị hàm số ta thấy hàm số đạt cực đại tại điểm x = 2 Câu 24: Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ. Số điểm cực trị của hàm số y = f(x) là: Đáp án D Dựa vào đồ thị hàm số y = f(x) ta thấy f'(x) có 1 lần đổi dấu từ âm sang dương ⇒ Hàm số y = f(x) có 1 điểm cực trị. Câu 25: Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu f'(x) như sau: Hàm số y = f(x) có bao nhiêu điểm cực trị? Đáp án C Dựa vào bảng biến thiên ta thấy hàm số đổi dấu khi đi qua 4 điểm có hoành độ là -1; 0; 2; 4. Vậy hàm số y = f(x) có 4 điểm cực trị. Câu 26: Tìm tất cả các giá trị của m để hàm số có cực đại và cực tiểu. Đáp án B TXĐ: D = R TH1: m=0→y=x−1 hàm số không có cực trị TH2: m≠0 Ta có: ⇒y'=mx2−2mx+1 Để hàm số đã cho có cực đại, cực tiểu thì phương trình y’ = 0 phải có 2 nghiệm phân biệt. ⇒Δ'=m2−m>0⇔[m<0m>1 Câu 27: Tìm tất cả các giá trị thực của tham số m để hàm số y=x3−3x2+(m+1)x+2 có hai điểm cực trị Đáp án C y=x3−3x2+(m+1)x+2⇒y'=3x2−6x+m+1 Hàm số y=x3−3x2+(m+1)x+2 có hai điểm cực trị ⇔y'=0 có hai nghiệm phân biệt. ⇔Δ'>0⇔32−3.(m+1)>0⇔m<2 Câu 28: Tìm tất cả các giá trị của m để đồ thị hàm số y=−x4+2mx2 có 3 điểm cực trị? Đáp án C y=−x4+2mx2⇒y'=−4x3+4mx=−4x(x2−m)⇒y'=0⇔[x=0x2=m Để hàm số có ba điểm cực trị thì phương trình y' = 0 có ba nghiệm phân biệt hay phương trình x2=m có hai nghiệm phân biệt khác 0 hay m > 0 Câu 29: Tìm tất cả các giá trị thực của m để hàm số y=x4+2(m2−9)x2+5m+2 có cực đại, cực tiểu Đáp án A Ta có: Hàm số đã cho có cực đại, cực tiểu khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0. ⇔9−m2>0⇔−3<m<3 Câu 30: Cho hàm số y=2x4−(m+1)x2−2. Tất cả các giá trị của m để hàm số có 1 điểm cực trị là: Đáp án D y'=8x3−2(m+1)x=2x[4x2−(m+1)]⇒y'=0⇔ [x=0 4x2 Ta có yêu cầu bài toán để hàm số có một điểm cực trị ⇔y'=0 có 1 nghiệm duy nhất ⇔(1) có 1 nghiệm x = 0 hoặc (1) vô nghiệm ⇔m+1≤0⇔m≤−1
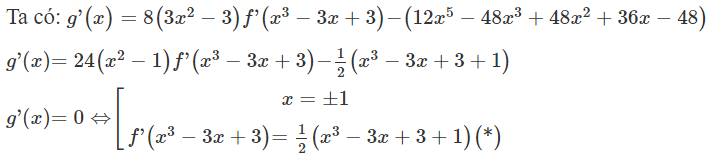

;∀x∈R. Số điểm cực trị của hàm số đã cho là:

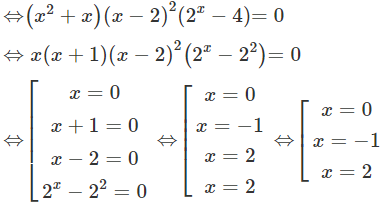


−3x+2⇒y'=3x2−3y'=0⇔x=±1





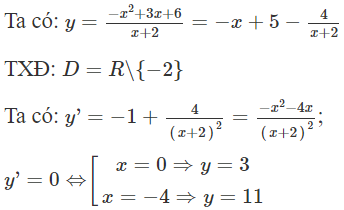
















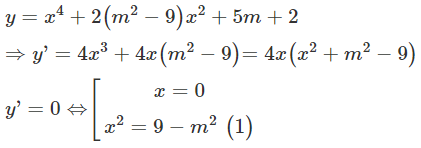

=m+1
Bài thi liên quan
-
Trắc nghiệm Cực trị của hàm số có đáp án (P2)
-
33 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (4056 lượt thi)
- 28 câu trắc nghiệm: Cực trị của hàm số có đáp án (1122 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (Nhận biết) (1292 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (Thông hiểu) (2165 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (Vận dụng) (1430 lượt thi)
Các bài thi hot trong chương
- 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số (8306 lượt thi)
- Bài tập về Tính đơn điệu của hàm số có lời giải (7417 lượt thi)
- Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (6533 lượt thi)
- Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (3475 lượt thi)
- 21 câu trắc nghiệm: Sự đồng biến nghịch biến của hàm số có đáp án (2240 lượt thi)
- Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (Nhận biết) (2235 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (Nhận biết) (1867 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (Thông hiểu) (1738 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (Vận dụng) (1710 lượt thi)
- Bài 1: Sự đồng biến, nghịch biến của hàm số (1683 lượt thi)
