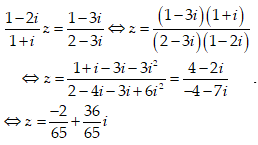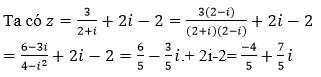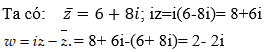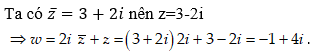30 câu hỏi trắc nghiệm thuộc 125 câu trắc nghiệm Số phức cơ bản-P1 (có đáp án)

Câu 1:

Cho hai số phức z₁= 3i - 2; z₂ = 5 + 3i. Tìm số phức z = z₁ + z₂.

A. 3 + 6i

B. 9 - i

C. -1 + 10i

D. 4 + 3i

Xem đáp án

Chọn A.

Ta có: z = z₁ + z₂= (-2 + 3i) + (5 + 3i) = (-2 + 5) + (3 + 3)i = 3 + 6i

Câu 2:

Cho số phức z = a + bi và $w = \frac{1}{2} (z + \bar{z})$ . Mệnh đề sau đây là đúng?

A. w là một số thực

B . w = 2

C. w là một số thuần ảo.

D. w = i

Xem đáp án

Chọn A.

Câu 3:

Cho hai số phức z₁ = 2 - 3i; z₂= 4i - 10. Tìm số phức z = z₁ – z₂.

A. z = 3 + 3i.

B. z = 12 - 7i.

C. z = 2 - 3i.

D. z = 3 - i.

Xem đáp án

Chọn B.

Ta có z = z₁ – z₂= (2 - 3i) - (4i - 10) = (2 + 10) + (-3 - 4)i = 12 - 7i.

Câu 4:

Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.

Xem đáp án

Chọn D.

Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo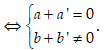

Câu 5:

Tìm số phức z thỏa mãn 3z - 3i = 6 - 9i

A. z = -1 + 2i

B. z = -3 + 2i

C. z = 1+ i

D. z = 2 - 2i

Xem đáp án

Chọn D.

Ta có 3z - 3i = 6 - 9i

Suy ra : 3z = 6 - 9i + 3i

Hay 3z = 6 + (-9 + 3)i = 6 – 6i

Do đó: z = 2 - 2i.

Câu 6:

Cho số phức z = 10i - 8. Tìm phần thực, phần ảo của số phức w = z - i

A. Phần thực bằng -8 và phần ảo bằng -8i

B. Phần thực bằng -2 và phần ảo bằng -3

C. Phần thực bằng 8 và phần ảo bằng 10i

D. Phần thực bằng – 8 và phần ảo bằng 9

Xem đáp án

Chọn D.

Ta có w = z - i = (10i - 8) - i = - 8 + 9i

w có phần thực bằng -8 và phần ảo bằng 9.

Câu 7:

Cho hai số phức z₁= 3i - 4; z₂ = 3 - i. Tìm số phức z = z₁ – z₂.

A. 6 - 5i

B. 7 + 4i

C. 4 + 4i

D. -7 + 4i

Xem đáp án

Chọn D.

Ta có z₁ - z₂ = (-4 + 3i) - ( 3 - i) = -7 + 4i.

Câu 8:

Cho hai số phức z = i. Tìm số phức w = z⁵.

A. w = i.

B. w = -1.

C. w = 1.

D. w = -i.

Xem đáp án

Chọn A.

Ta có: w = z⁵ = i⁵ = i⁴ .i = 1.i = i.

Câu 9:

Cho hai số phức z₁= 1 + i; z₂= 1 - 2i. Tìm số phức z = z₁.z₂.

A. z = 1.

B. z = 3 - i.

C. z = -1 + i.

D. z = -2 + i.

Xem đáp án

Chọn B.

Ta có z = z₁.z₂= (1 + i) .(1 - 2i) = 1 - 2i + i - 2i²= 3 - i.

Câu 10:

Cho 2 số phức z₁= 2 + 2i; z₂ = 4 - 5i .Tìm phần ảo của số phức w = z₁.z₂

A. 4.

B. -1.

C. -2.

D. 1.

Xem đáp án

Chọn C.

Ta có w = (2 + 2i)(4 - 5i) = 8 - 10i + 8i - 10i²= 18 - 2i.

Vậy phần ảo của số phức w là -2.

Câu 11:

Cho hai số phức z₁= 1 - i; z₂= 5 - 2i . Tìm phần ảo của số phức $z = z_{1}^{2} - z_{2}^{2}$

A. b = -4.

B. b = 8.

C. b = 0.

D. b = -21.

Xem đáp án

Chọn B.

Ta có z = (1- i)²- (5 - 2i)²= 1 - 2i + i²- ( 25 - 10i + 4i²) = -21 + 8i.

Vậy phần ảo của số phức z là 8.

Câu 12:

Cho hai số phức z₁= 1 + i; z₂= 4 - i. Tim số phức $z = z_{1}^{2} . z_{2}$

A. z = 2 + 8i.

B. z = 2 - 8i.

C. z = 5 + 3i.

D. z = 3 + 3i.

Xem đáp án

Chọn A.

Ta có z = (1 + i)² (4 - i) = (1 + 2i + i²)(4 - i) = 2i.(4 - i) = 8i - 2i²= 2 + 8i.

Câu 13:

Tìm phần thực của số phức $z = \frac{4 + 2 i}{2 - i}$

A. 3/5.

B. 8/5.

C. 6/5.

D. Đáp án khác.

Xem đáp án

Chọn C.

Ta có:

$z = \frac{4 + 2 i}{2 - i} = \frac{(4 + 2 i) (2 + i)}{4 - i^{2}} = \frac{8 + 8 i + 2 i^{2}}{5} = \frac{6 + 8 i}{5} = \frac{6}{5} + \frac{8}{5} i$

Vậy phần thực của số phức z là $\frac{6}{5} .$

Câu 14:

Tìm số phức $z = \frac{3 - 4 i}{4 - i}$

A.

B.

C.

D.

Xem đáp án

Chọn A.

Ta có:

$z = \frac{3 - 4 i}{4 - i} = \frac{(3 - 4 i) (4 + i)}{(4 - i) (4 + i)} = \frac{(3 - 4 i) (4 + i)}{17} = \frac{12 + 3 i - 16 i - 4 i^{2}}{17} = \frac{16}{17} - \frac{13}{17} i$

Câu 15:

Tìm số phức z thỏa mãn $\frac{1 - 2 i}{1 + i} z = \frac{1 - 3 i}{2 - 3 i}$

A.

B.

C.

D.

Xem đáp án

Chọn A.

Ta có:

Câu 16:

Tìm số phức $z = \frac{3}{2 + i} + 2 i - 2$

A.

B.

C.

D.

Xem đáp án

Chọn D.

Câu 17:

Cho số phức z = 6 - 8i. Tìm số phức $w = i z - \bar{z}$

A. w = -3 + 2i.

B. w = 2 + 2i.

C. w = -2 - 2i.

D. w = 2 - 2i.

Xem đáp án

Chọn D.

Câu 18:

Cho số phức $\bar{z} = 3 + 2 i$ . Tìm số phức $w = 2 i \bar{z} + z$

A. w = -1 + 4i.

B. w = 9 - 2i.

C. w = 4 + 7i.

D. w = 4 - 7i.

Xem đáp án

Chọn A.

Câu 19:

Tìm số phức z thỏa mãn $(2 + i) z = (3 - 2 i) \bar{z} - 4 (1 - i)$

A. z = 3 - i.

B. z = -3 - i.

C. z = 3 + i.

D. z = -3 + i.

Xem đáp án

Chọn A.

Đặt z = a + bi (a, b $\in$ R), suy ra $\bar{z} = a - b i$

Khi đó ta có

Câu 20:

Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.

A.

B.

C.

D.

Xem đáp án

Chọn B.

Ta có: (2 - 3i).(1 + 2i) = 2 + 4i - 3i - 6i²= 8 + i

Từ giả thiết : (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i nên

(1 + i)z + (8 + i) = 7 + 3i hay (1 + i)z = -1 + 2i

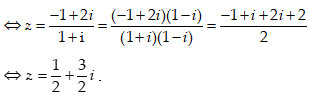
Câu 21:

Tìm phần thực a của số phức z thỏa mãn (1 + i) ²( 2 - i) z = 8 + i + (1 + 2i) z.

A. a = 2.

B. a = -3.

C. a = -2.

D. a = 3.

Xem đáp án

Chọn A.

Ta có: (1 + i) ²( 2 - i) z = 8 + i + (1 + 2i) z.

Suy ra: (2 + 4i)z - (1 + 2i)z = 8 + i

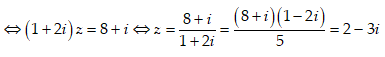
Vậy phần thực của z bằng 2.

Câu 22:

Tìm số phức z =(2 - i) ³- ( 2i + 1) ²

A. z= -5 + 15i.

B. z = 5 - 15i.

C. z = 3 - 8i.

D. z = 3 + 8i.

Xem đáp án

Chọn B.

Ta có: z = ( 2 - i) ³- ( 2i + 1) ²

Hay z = 8 - 12i + 6i²- i³- ( 4i²+ 4i + 1)

z = 8 - 12i - 6 + i + 4 - 4i - 1 = 5 - 15i.

Câu 23:

Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức $w = i z + \bar{z}$

A. w = 10 - 10i.

B. w = -3 - 3i.

C. w = 16 - 16i.

D. w = -16 - 16i.

Xem đáp án

Chọn D.

+ Do z = (1 - i)(2i - 8) = 2i + 2 - 8 + 8i hay z = -6 + 10i

Khi đó:và iz = -10 - 6i

Khi đó: w = ( -10 - 6i) + ( -6 -10i) = -16 - 16i.

Câu 24:

Cho số phức z = ( 2 + i)( 3 - i). Tìm phần thực a và phần ảo b của số phức $\bar{z}$

A. a = 7 ; b = 1.

B. a = 7 ; b = -1.

C. a = - 7; b = 1.

D. a = -7; b = - 1.

Xem đáp án

Chọn B.

Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i²= 7 + i

Nên

Vậy phần thực bằng a = 7 và phần ảo b = -1.

Câu 25:

Tìm số phức liên hợp của số phức $z = \frac{1 + i}{2 - i}$

A.

B.

C.

D.

Xem đáp án

Chọn B.

Câu 26:

Tìm số phức z thỏa mãn $z - (2 + 3 i) \bar{z} = 1 - 9 i$

A. z = -3 - i.

B. z = -2 - i.

C. z = 2 - i.

D. z = 2 + i.

Xem đáp án

Chọn C.

Gọi z = a + bi

Từ giả thiết ta suy ra: a + bi - 2a + 2bi - 3ai - 3b = 1 - 9i

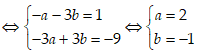
Vậy z = 2 - i.

Câu 27:

Cho số phức $z = \frac{4 - 8 i}{1 + i}$ . Tìm phần thực a và phần ảo b của số phức $\bar{z}$

A. a = 2; b = 6.

B. a = -2; b = -6.

C. a = -2; b = 6.

D. a = 2; b = -3.

Xem đáp án

Chọn C.

Theo giả thiết ta có:

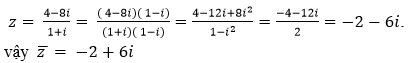
⇒ Phần thực a = -2 và phần ảo bằng b = 6.

Câu 28:

Tìm số phức liên hợp của số phức $z = (1 + i) (3 - 2 i) + \frac{1}{2 + i}$

A.

B.

C.

D.

Xem đáp án

Chọn C.

Câu 29:

Tìm tổng phần thực và phần ảo của số phức z thỏa mãn $z + 2 \bar{z} = {(2 - i)}^{3} (1 - i)$

A. 13.

B. – 3.

C.10.

D. -10.

Xem đáp án

Chọn C.

Đặt z = x + yi

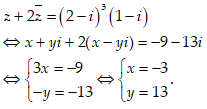
Tổng phần thực và phần ảo của số phức z là -3+ 13 = 10.

Câu 30:

Tìm các số phức z thỏa mãn ${|z|}^{2} + 2 z \bar{z} + {|\bar{z}|}^{2} = 8$ và $z + \bar{z} = 2$

A. z₁= -1 + i; z₂= 1 - i.

B. z₁= 1 + i; z₂= -1 - i.

C. z₁= -1 + i; z₂= -1 - i.

D. z₁= 1 + i; z₂= 1 - i.

Xem đáp án

Chọn D.

Đặt z = x + yi (với x, y $\in$ R)

Vậy các số phức cần tìm là

$z_{1} = 1 + i v à z_{2} = 1 - i$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

125 câu trắc nghiệm Số phức cơ bản (có đáp án)

125 câu trắc nghiệm Số phức cơ bản-P1 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương