Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 67)
-
1453 lượt thi
-
86 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Điền số thích hợp vào chỗ trống:
a) 1 m2 = ... dm2
b) 15 m2 = ... cm2
c) 2 m2 5 dm2 = ... dm2
d) 4 m2 6 dm2 9 cm2 = ... cm2
 Xem đáp án
Xem đáp án
a) 1 m2 = 100 dm2
b) 15 m2 = 1500 cm2
c) 2 m2 5 dm2 = 205 dm2
d) 4 m2 6 dm2 9 cm2 = 40609 cm2
Câu 2:
Điền số thích hợp vào chỗ trống:
a) 1 km2 + 4 km2 = ... km2
b) 8 dm2 + 40 cm2 = ... cm2
 Xem đáp án
Xem đáp án
a) 1 km2 + 4 km2 = 5 km2
b) 8 dm2 + 40 cm2 = 840 cm2
Câu 3:
Cho tam giác ABC có G là trọng tâm. Chứng minh diện tích tam ABC gấp 3 lần diện tích tam giác AGC.
 Xem đáp án
Xem đáp án
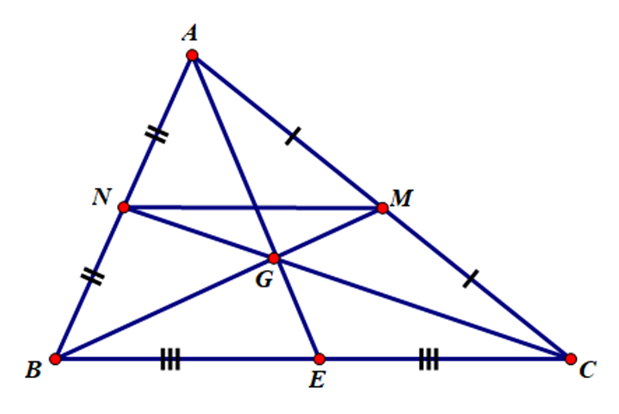
Gọi N, M, E lần lượt là trung điểm của AB, AC và BC.
Suy ra CN, BM, AE là các đường trung tuyến của ΔABC
Do đó, CN, BM, AE cắt nhau tại G.
Áp dụng tính chất đường trung tuyến trong tam giác ta có:
\[CG = \frac{2}{3}CN\]
Xét ΔAGC và ΔANC có cùng đường cao hạ từ A xuống NC
Mà đáy \[CG = \frac{2}{3}CN\]
Suy ra \[{S_{AGC}} = \frac{2}{3}{S_{ANC}}\] (1)
Xét ΔANC và ΔABC có cùng chung chiều cao hạ từ C xuống AB
Mà đáy \[AN = \frac{1}{2}AB\] (vì N là trung điểm của AB)
Suy ra \[{S_{ANC}} = \frac{1}{2}{S_{ABC}}\] (2)
Từ (1) và (2) ta có: \[{S_{AGC}} = \frac{2}{3} \cdot \frac{1}{2}{S_{ABC}} = \frac{1}{3}{S_{ABC}}\]
Vậy diện tích tam ABC gấp 3 lần diện tích tam giác AGC.
Câu 4:
Cho tam giác ABC có G là trọng tâm. So sánh diện tích tam giác AGB, BGC và CGA.
 Xem đáp án
Xem đáp án
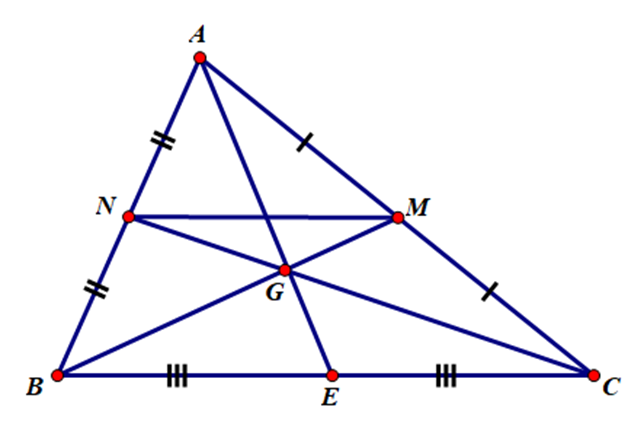
Gọi N, M, E lần lượt là trung điểm của AB, AC và BC.
Suy ra CN, BM, AE là các đường trung tuyến của ΔABC
Do đó, CN, BM, AE cắt nhau tại G.
Áp dụng tính chất đường trung tuyến trong tam giác ta có:
\[AG = \frac{2}{3}AE;\,\,BG = \frac{2}{3}BM;\,\,CG = \frac{2}{3}CN\]
Xét ΔAGB và ΔAEB có cùng đường cao hạ từ B xuống AE
Mà đáy \[AG = \frac{2}{3}AE\]
Suy ra \[{S_{AGB}} = \frac{2}{3}{S_{AEB}}\] (1)
Xét ΔAEB và ΔABC có cùng chung chiều cao hạ từ A xuống BC
Mà đáy \[BE = \frac{1}{2}BC\] (vì E là trung điểm của BC)
Suy ra \[{S_{AEB}} = \frac{1}{2}{S_{ABC}}\] (2)
Từ (1) và (2) ta có: \[{S_{AGC}} = \frac{2}{3} \cdot \frac{1}{2}{S_{ABC}} = \frac{1}{3}{S_{ABC}}\]
Chứng minh tương tự ta có: \[{S_{AGC}} = \frac{1}{3}{S_{ABC}};\,\,{S_{BGC}} = \frac{1}{3}{S_{ABC}}\]
Suy ra \[{S_{AGB}} = \,\,{S_{BGC}} = {S_{AGC}} = \frac{1}{3}{S_{ABC}}\]
Vậy \[{S_{AGB}} = \,\,{S_{BGC}} = {S_{AGC}}\].
Câu 5:
Giải phương trình: (2x – 1)3 = –8
 Xem đáp án
Xem đáp án
Ta có: (2x – 1)3 = –8
⇔ (2x – 1)3 = (–2)3
⇔ 2x – 1 = –2
⇔ 2x = –2 + 1
⇔ 2x = –1
Vậy phương trình đã cho có nghiệm là \[x = - \frac{1}{2}\].
Câu 6:
Giải phương trình: (2x + 1)2 = 4
 Xem đáp án
Xem đáp án
Ta có: (2x + 1)2 = 4
⇔ (2x + 1)2 = 22 = (–2)2
⇔ 2x + 1 = 2 hoặc 2x + 1 = –2
⇔ 2x = 2 – 1 hoặc 2x = –2 – 1
⇔ 2x = 1 hoặc 2x = –3
⇔ \[x = \frac{1}{2}\] hoặc \[x = \frac{{ - 3}}{2}\]
Vậy tập nghiệm của phương trình đã cho là \[S = \left\{ {\frac{1}{2};\,\,\frac{{ - 3}}{2}} \right\}\].
Câu 9:
Cho dãy số 2; 4; 6; 8; 10;...; 1992. Hỏi số thứ 2000 của dãy số là chữ số nào?
 Xem đáp án
Xem đáp án
Khoảng cách giữa các số trong dãy là:
4 – 2 = 2
Số thứ 2000 là:
2000 × 2 = 4000
Đáp số: 4000
Câu 10:
Giải phương trình: 2x-2 = 8
 Xem đáp án
Xem đáp án
2x-2 = 8
⇔ 2x-2 = 23
⇔ x – 2 = 3
⇔ x = 5
Vậy nghiệm của phương trình đã cho là x = 5.
Câu 11:
Giải phương trình: 3x + 2 = 27
 Xem đáp án
Xem đáp án
3x + 2 = 27
⇔ 3x + 2 = 33
⇔ x + 2 = 3
⇔ x = 1
Vậy nghiệm của phương trình đã cho là x = 1.
Câu 12:
Tính nhanh A = (315.3 + 372.3 + 372.7 + 315.7): (26.13 + 74.14)
 Xem đáp án
Xem đáp án
Ta có: (315.3 + 372.3 + 372.7 + 315.7): (26.13 + 74.14)
\[ = \frac{{(315 + 372).3 + (372 + 315).7}}{{26.13 + 74.14}}\]
\[ = \frac{{(315 + 372)(3 + 7)}}{{2.13.13 + 74.2.7}}\]
\[ = \frac{{687.10}}{{2(169 + 518)}}\]
\[ = \frac{{6870}}{{2.687}} = \frac{{6870}}{{1374}} = 5\]
Vậy A = 5
Câu 15:
Tính: A = (72005 + 72004) : 72004
 Xem đáp án
Xem đáp án
A = (72005 + 72004) : 72004
A = (7 + 1)72004 : 72004
A = 8
Vậy A = 8
Câu 16:
Tính: B = (122023 – 122022 + 122021) : 122021
 Xem đáp án
Xem đáp án
B = (122023 – 122022 + 122021) : 122021
B = (122 – 12 + 1)122021 : 122021
B = 122 – 12 + 1
B = 144 – 12 + 1
B = 132 + 1
B = 133
Vậy B = 133
Câu 17:
Tìm x:
7x – 2x = 611 : 69 + 44 : 11
 Xem đáp án
Xem đáp án
7x – 2x = 611 : 69 + 44 : 11
5x = 62 + 4
5x = 36 + 4
5x = 40
x = 40 : 5
x = 8
Vậy x = 8
Câu 18:
Tìm x:
15x + 5x = 5100 : 597 – 60 : 12
 Xem đáp án
Xem đáp án
15x + 5x = 5100 : 597 – 60 : 12
20x = 53 – 5
20x = 125 – 5
20x = 120
x = 120 : 20
x = 6
Câu 19:
Biết rằng 8 công nhân làm trong 6 giờ được 144 sản phẩm. Hỏi 12 công nhân làm trong bao nhiêu giờ thì được 180 sản phẩm?
 Xem đáp án
Xem đáp án
8 công nhân làm trong 1 giờ được số sản phẩm là:
144 : 6 = 24 (sản phẩm)
1 công nhân làm 1 giờ được số sản phẩm là:
24 : 8 = 3 (sản phẩm)
12 công nhân làm 1 giờ được số sản phẩm là:
3 × 12 = 36 (sản phẩm)
12 công nhân làm 180 sản phẩm trong số giờ là:
180 : 36 = 5 (giờ)
Đáp số: 5 giờ
Câu 20:
Biết rằng 3 công nhân làm trong 6 giờ thì hoàn thành 1 công việc. Hỏi 9 công nhân làm trong bao nhiêu giờ thì hoàn thành công việc?
 Xem đáp án
Xem đáp án
9 công nhân gấp 3 công nhân số lần là:
9 : 3 = 3 (lần)
9 công nhân làm việc trong số giờ thì hoàn thành là:
6 : 3 = 2 (giờ)
Đáp số: 2 giờ
Câu 21:
Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD lần lượt tai M, N. Chứng minh OM = ON.
 Xem đáp án
Xem đáp án
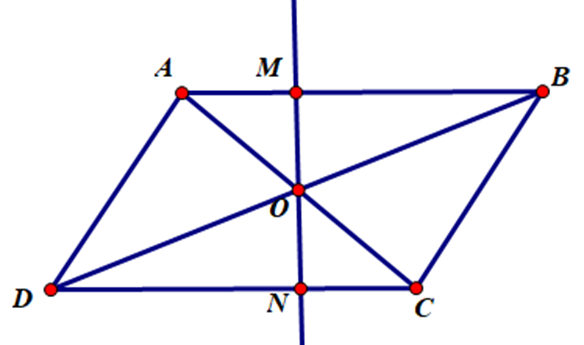
Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm mỗi đường.
Suy ra O là trung điểm của AC và BD hay OA = OC và OB = OD
Xét ΔAMO và ΔCNO có:
\[\widehat {MAO} = \widehat {NCO}\] (vì 2 góc so le trong)
OA = OC
\[\widehat {MOA} = \widehat {NOC}\] (vì 2 góc đối đỉnh)
Suy ra ΔAMO = ΔCNO (g.c.g)
Do đó OM = ON
Vậy OM = ON.
Câu 22:
Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD lần lượt tai M, N. Chứng minh: Tứ giác BMDN là hình bình hành.
 Xem đáp án
Xem đáp án
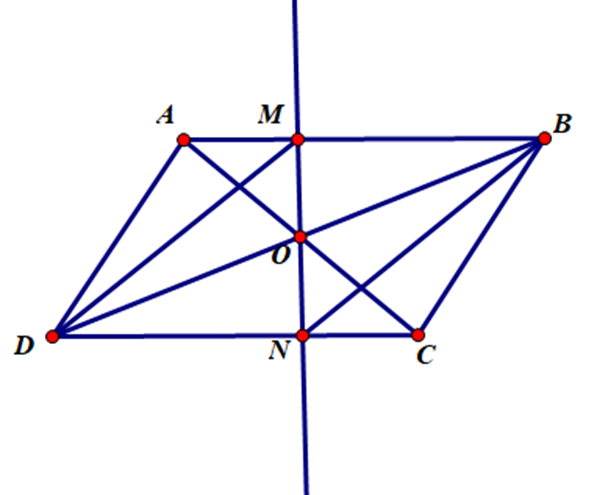
Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm mỗi đường.
Suy ra O là trung điểm của AC và BD hay OA = OC và OB = OD
Xét ΔAMO và ΔCNO có:
\[\widehat {MAO} = \widehat {NCO}\] (vì 2 góc so le trong)
OA = OC
\[\widehat {MOA} = \widehat {NOC}\] (vì 2 góc đối đỉnh)
Suy ra ΔAMO = ΔCNO (g.c.g)
Do đó OM = ON
Xét tứ giác DMBN có:
Đường chéo BD và MN cắt nhau tại O
Mà O là trung điểm của MN (do OM=ON) và O là trung điểm của BD
Suy ra DMBN là hình bình hành.
Vậy DMBN là hình bình hành.
Câu 23:
Từ bốn chữ số 2, 5, 7, 9. Viết được tất cả bao nhiêu số tự nhiên có bốn chữ số mà các chữ số đó đều khác nhau?
 Xem đáp án
Xem đáp án
Có 4 cách chọn chữ số hàng nghìn (chọn 2; 5; 7; 9)
Sau khi chọn chữ số hàng nghìn thì còn 3 cách chọn chữ số hàng trăm.
Sau khi chọn chữ số hàng nghìn và hàng trăm thì còn 2 cách chọn chữ số hàng trục.
Cuối cùng còn 1 cách chọn chữ số hàng đơn vị.
Vậy ta viết được tất cả:
4 ×3 × 2 × 1 = 24 (số)
Vậy từ bốn chữ số 2, 5, 7, 9 viết được 24 số tự nhiên có bốn chữ số mà các chữ số đó đều khác nhau.
Câu 24:
Từ các chữ số 0, 2, 4, 6 lập được bao nhiêu số có 3 chữ số khác nhau. Tính tổng các số đó.
 Xem đáp án
Xem đáp án
Gọi số có 3 chữ số khác nhau: \[\overline {abc} \] ( a, b, c Î ℕ*, a ¹ 0)
a có 3 cách chọn
b có 3 cách chọn
c có 2 cách chọn
Do đó, từ các số 0; 2; 4; 6 ta có thể lập được tất cả số có 3 chữ số khác nhau là:
3 × 3 × 2 = 18 số
Suy ra 18 số cần tìm là: 246; 264; 240; 204; 260; 206; 426; 462; 420; 402; 460; 406; 624; 642; 640; 604; 620; 602.
Ta thấy rằng:
Các số 2; 4; 6 xuất hiện ở hàng trăm là 6 lần.
Các số 2; 4; 6 xuất hiện ở hàng chục là 4 lần.
Các số 2; 4; 6 xuất hiện ở hàng đơn vị là 4 lần.
Số 0 xuất hiện ở hàng chục là 6 lần.
Số 0 xuất hiện ở hàng đơn vị là 6 lần.
Vậy tổng các số là: (Số 0 ở đây không cần cộng vào)
(2 + 4 + 6) × 100 × 6 + (2 + 4 + 6) × 10 × 4 + (2 + 4 + 6) × 1 × 4
= 12 × (100 × 6 + 10 × 4 + 4)
= 12 × 644
= 7728
Đáp số: 7728
Câu 25:
Cho dãy số: 1; 2; 3; 4;.........;124; 125. Hỏi dãy số có bao nhiêu chữ số?
 Xem đáp án
Xem đáp án
Ta chia dãy số trên theo nhóm:
(1, 2,..., 9), (10, 11,..., 99), (100, 101,...., 125)
Số các số ở nhóm có 1 chữ số là:
(9 – 1) : 1 + 1 = 9 (số)
Số các số ở nhóm có hai chữ số là:
(99 – 10) : 1 + 1 = 90 (số)
Số các số ở nhóm có 3 chữ số là:
(125 – 100) : 1 + 1 = 26 (số)
Dãy trên có số chữ số là:
1 × 9 + 2 × 90 + 3 × 26 = 267 (chữ số)
Đáp số: 267 chữ số
Câu 26:
Cho dãy số 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, .... Hỏi chữ số đứng ở vị trí thứ 30 trong dãy trên là chữ số nào ?
 Xem đáp án
Xem đáp án
Ta có: 30 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 2
Ta phân tích như vậy bởi có 1 số 1, 2 số 2, 3 số 3 ...
Vậy số thứ ba mươi sẽ là số thứ 2 đằng sau số 7 cuối cùng có nghĩa là đó là số 8 thứ 2
Vậy số thứ 30 là số 8.
Câu 27:
Cho tam giác ABC, điểm D là nằm trên cạnh BC. Qua D lần lượt kẻ các đường thẳng song song với AC, AB và cắt AB, AC theo thứ tự ở E, F. Biết diện tích của tam giác BED là 16 cm2, diện tích tam giác FDC bằng 25 cm2. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
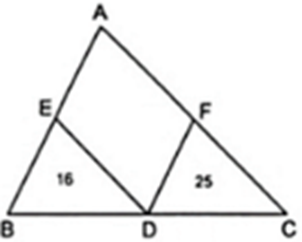
Xét ΔEBD và ΔABC có:
\[\widehat B\] chung
DE // AC nên \[\widehat {BDE} = \widehat C\](vì đồng vị)
Do đó ΔEBD ᔕ ΔABC (g.g)
Áp dụng tính chất của tỉ số đồng dạng ta có:
\[{\left( {\frac{{BD}}{{BC}}} \right)^2} = \frac{{{S_{EBD}}}}{{{S_{ABC}}}} = \frac{{16}}{{{S_{ABC}}}} = {\left( {\frac{4}{{\sqrt {{S_{ABC}}} }}} \right)^2}\]
\[{m_a} = \sqrt {\frac{{2{b^2} + 2{c^2} - {a^2}}}{4}} = 9\]
Xét ΔFDC và ΔABC có:
\[\widehat C\] chung
DF // AB nên \[\widehat {FDC} = \widehat B\](vì đồng vị)
Do đó ΔFDC ᔕ ΔABC (g.g)
Áp dụng tính chất của tỉ số đồng dạng ta có:
\[{\left( {\frac{{DC}}{{BC}}} \right)^2} = \frac{{{S_{FDC}}}}{{{S_{ABC}}}} = \frac{{25}}{{{S_{ABC}}}} = {\left( {\frac{5}{{\sqrt {{S_{ABC}}} }}} \right)^2}\]
\[ \Rightarrow \frac{{DC}}{{BC}} = \frac{5}{{\sqrt {{S_{ABC}}} }}\]
Do đó:
\[ \Rightarrow \frac{{BD}}{{BC}} + \frac{{DC}}{{BC}} = \frac{4}{{\sqrt {{S_{ABC}}} }} + \frac{5}{{\sqrt {{S_{ABC}}} }} = \frac{9}{{\sqrt {{S_{ABC}}} }}\]
\[ \Rightarrow 1 = \frac{9}{{\sqrt {{S_{ABC}}} }}\]
\[ \Rightarrow \sqrt {{S_{ABC}}} = 9\]
Þ SABC = 81 cm2
Vậy SABC = 81 cm2.
Câu 28:
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A là trung điểm của CI.
 Xem đáp án
Xem đáp án
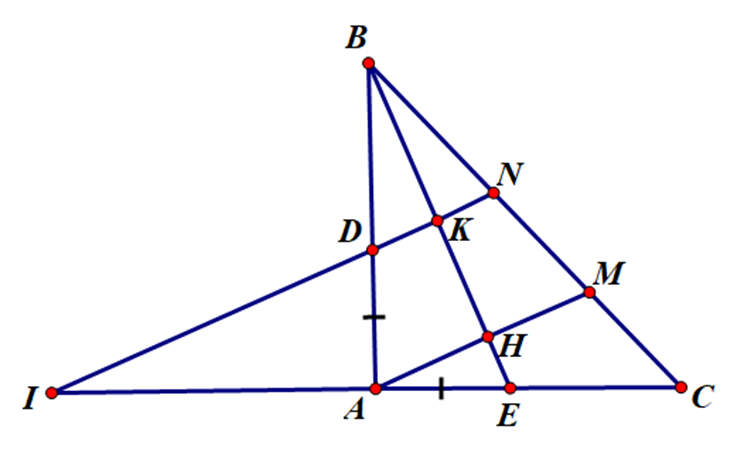
Gọi K là giao điểm của DN và BE
Xét ΔBDK vuông tại K có: \[\widehat {BDK} + \widehat {DBK} = 90^\circ \]
Xét ΔABE vuông tại A có: \[\widehat {ABE} + \widehat {BEA} = 90^\circ \]
Suy ra \[\widehat {BDK} = \widehat {BEA}\]
Mà \[\widehat {BDK} = \widehat {IDA}\] (vì hai góc đối đỉnh)
Suy ra \[\widehat {BEA} = \widehat {IDA}\]
Xét ΔDAI và ΔEAB có:
AD = AE
\[\widehat {IDA} = \widehat {BEA}\]
\[\widehat {IAD} = \widehat {BAE}\, = 90^\circ \]
Suy ra ΔDAI = ΔEAB (cạnh góc vuông – góc nhọn)
Do đó AI = AB
Mà AB = AC nên AI = AC
Vậy A là trung điểm của CI.
Câu 29:
Cho tam giác ABC vuông tại A, AB = AC. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh MC = MN.
 Xem đáp án
Xem đáp án
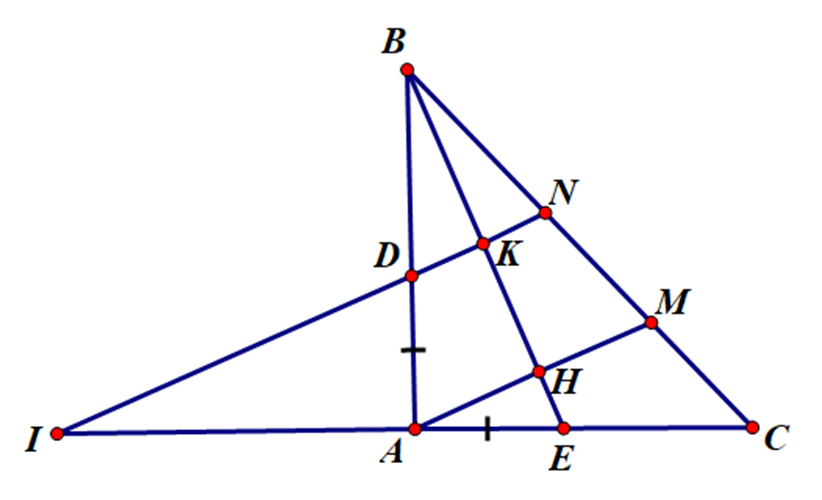
Ta có: AM // IN (vì cùng vuông góc với BE)
Gọi K là giao điểm của DN và BE
Xét ΔBDK vuông tại K có: \[\widehat {BDK} + \widehat {DBK} = 90^\circ \]
Xét ΔABE vuông tại A có: \[\widehat {ABE} + \widehat {BEA} = 90^\circ \]
Suy ra \[\widehat {BDK} = \widehat {BEA}\]
Mà \[\widehat {BDK} = \widehat {IDA}\] (vì hai góc đối đỉnh)
Suy ra \[\widehat {BEA} = \widehat {IDA}\]
Xét ΔDAI và ΔEAB có:
AD = AE
\[\widehat {IDA} = \widehat {BEA}\]
\[\widehat {IAD} = \widehat {BAE}\, = 90^\circ \]
Suy ra ΔDAI = ΔEAB (cạnh góc vuông – góc nhọn)
Do đó AI = AB
Mà AB = AC nên AI = AC
Xét ΔINC có:
AI = AC
AM // IN
Suy ra MN = MC (hệ quả của tính chất đường trung bình trong tam giác)
Vậy MN = MC
Câu 30:
Cho tam giác ABC. Gọi ma là độ dài đường trung tuyến xuất phát từ đỉnh A.
Chứng minh \[{m_a} = \sqrt {\frac{{2{b^2} + 2{c^2} - {a^2}}}{4}} \]
 Xem đáp án
Xem đáp án
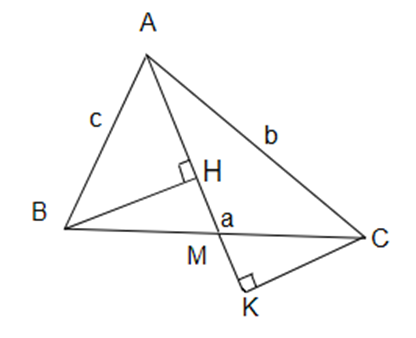
Gọi M là trung điểm của BC
Þ AM là đường trung tuyến xuất phát từ đỉnh A hay AM = ma.
Đặt AB = c, BC = a, CA = b.
Kẻ BH ^ AM, CK ^ AM
Þ BH // CK
\[ \Rightarrow \frac{{BH}}{{CK}} = \frac{{MB}}{{MC}} = \frac{{MH}}{{MK}} = 1\] (áp dụng định lý Ta-lét)
Þ MH = MK
Ta có: BC2 = (BM + MC)2 = (2BM)2 = 4BM2
Áp dụng định lý Py-ta-go vào tam giác vuông AHB, ta có:
AB2 = AH2 + HB2
Áp dụng định lý Py-ta-go vào tam giác vuông MHB, ta có:
BM2 = HM2 + HB2
Þ 2AB2 – 2BM2 = 2(AH2 + HB2) – 2(HM2 + HB2)
= 2AH2 – 2HM2 = 2(AH + MH)(AH – MH)
Þ 2AB2 – 2BM2 = 2. AM. (AH – MH) (1)
Áp dụng định lý Py-ta-go cho tam giác vuông AKC, ta có:
AC2 = AK2 + KC2
Áp dụng định lý Py-ta-go cho tam giác vuông MKC, ta có:
CM2 = KM2 + KC2
Þ 2AC2 – 2CM2 = 2(AK2 + KC2) – 2(KM2 + KC2)
= 2AK2 – 2KM2 = 2(AK + MK)(AK – MK)
Þ 2AC2 – 2CM2 = 2. AM. (AK + MK) (2)
Từ (1) và (2) ta có:
2AB2 – 2BM2 + 2AC2 – 2CM2 = 2. AM. (AH – MH) + 2. AM. (AK + MK)
Þ 2AB2 + 2AC2 – 4BM2 = 2. AM. (AH – MH + AK + MK)
Þ 2AB2 + 2AC2 – BC2 = 2. AM. 2AM (vì MH = MK) = 4AM2
Þ 2c2 + 2b2 – a2 = 4ma2 hay \[{m_a} = \sqrt {\frac{{2{b^2} + 2{c^2} - {a^2}}}{4}} \]
Vậy \[{m_a} = \sqrt {\frac{{2{b^2} + 2{c^2} - {a^2}}}{4}} \].
Câu 31:
Cho tam giác ABC, M. Gọi G là trọng tâm tam giác. Qua G kẻ đường thẳng d cắt 2 cạnh AB và AC.Gọi AA', BB', CC" là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. Gọi H là trung điểm của B’C’. Chứng minh: BB' + CC’ = 2MH.
 Xem đáp án
Xem đáp án
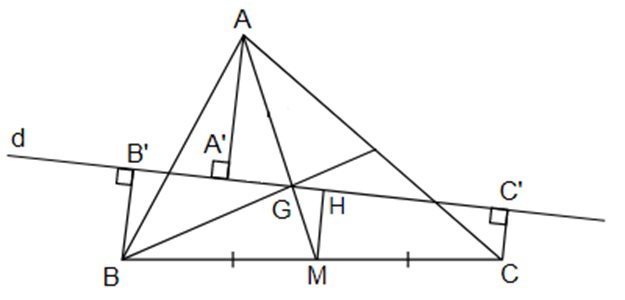
Xét hình thang BB'C'C:
M là trung điểm BC
H là trung điểm của B’C’
Þ MH là đường trung bình hình thang BB'C'C
\[ \Rightarrow MH = \frac{1}{2}(BB' + CC')\,\,\,\]
Vậy BB' + CC’ = 2MH.
Câu 32:
Cho tam giác ABC, trung tuyến AM. Gọi G là trọng tâm tam giác. Qua G kẻ đường thẳng d cắt 2 cạnh AB và AC.Gọi AA', BB', CC" là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. Chứng minh: AA' = BB' + CC’.
 Xem đáp án
Xem đáp án
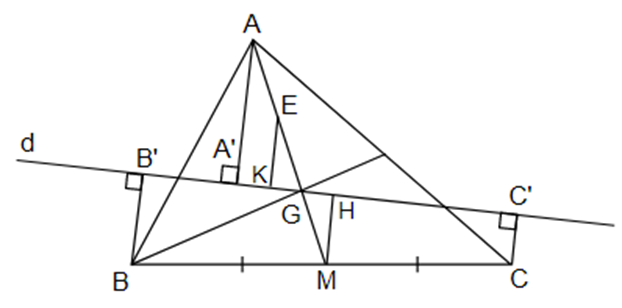
Gọi E là trung điểm của AG
Þ \[EA = EG = \frac{1}{2}AG\]
Từ E và M kẻ 2 đường thẳng song song với AA’ và cắt đường thẳng d lần lượt tại K và H.
Mà AA’ ^ d Þ EK ^ d và MH ^ d
G là trọng tâm ΔABC, AM là trung tuyến
\[MG = \frac{1}{2}AG\] (tính chất trọng tâm trong tam giác)
Xét ΔEKG và ΔMHG có:
\[\widehat {EKG} = \widehat {MHG} = 90^\circ \]
\[\widehat {EGK} = \widehat {MGH}\] (vì hai góc đối đỉnh)
\[EG = MG = \frac{1}{2}AG\]
Þ ΔEKG = ΔMHG (cạnh huyền – góc nhọn)
Þ EK = MH
Xét ΔAA'G:
E là trung điểm AG;
EK // AA'
Þ K là trung điểm A'G (tính chất đường trung bình trong tam giác)
Hay EK là đường trung bình của ΔAA'G nên \[EK = \frac{1}{2}AA'\]
\[ \Rightarrow MH = EK = \frac{1}{2}AA'\,\,\,(1)\]
Xét hình thang BB'C'C:
M là trung điểm BC
MH // BB' // CC'
Þ MH là đường trung bình hình thang BB'C'C
\[ \Rightarrow MH = \frac{1}{2}(BB' + CC')\,\,\,(2)\]
Từ (1) và (2) ta có: AA' = BB' + CC' (đpcm)
Vậy AA' = BB' + CC'.
Câu 33:
Có 5 người ăn trong 8 ngày hết 24 ki-lô-gam gạo. Hỏi 7 người ăn trong 10 ngày thì hết bao nhiêu ki-lô-gam gạo? Biết rằng khẩu phần ăn của mỗi người là như nhau.
 Xem đáp án
Xem đáp án
5 người ăn trong 10 ngày hết số ki-lô-gam gạo là:
10 × 24 : 8 = 30 (kg)
1 người ăn trong 10 ngày hết số ki-lô-gam gạo là:
30 : 5 = 6 (kg)
7 người ăn trong 10 ngày hết số ki-lô-gam gạo là:
7 × 6 = 42 (kg)
Đáp số: 42 kg
Câu 34:
Hai người 10 ngày ăn hết 10 kg gạo. Hỏi với mức ăn như thế, 4 người ăn 10 ngày hết bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Một người trong 10 ngày ăn hết số gạo là:
10 : 2 = 5 (kg)
4 người ăn hết số kg gạo trong 10 ngày là:
5 × 4 = 20 (kg)
Đáp số: 20 kg
Câu 35:
Xe thứ nhất được 12 tấn thóc, xe thứ 2 chở được ít hơn xe thứ nhất 2 tấn thóc. Vậy hai xe chở được bao nhiêu tấn thóc?
 Xem đáp án
Xem đáp án
Xe thứ 2 chở được số tấn thóc là:
12 – 2 = 10 (tấn)
Cả 2 xe chở được số tấn thóc là:
12 + 10 = 22 (tấn)
Đáp số: 22 tấn
Câu 36:
Xe thứ nhất chở được 8 tấn thóc, xe thứ hai chở nhiều hơn xe thứ nhất 4 tạ thóc. Xe thứ ba chở được số thóc bằng \[\frac{1}{4}\] số thóc mà xe thứ nhất và xe thứ hai chở được. Vậy cả ba xe chở được bao nhiêu tạ thóc?
 Xem đáp án
Xem đáp án
Đổi 8 tấn = 80 tạ
Xe thứ hai chở được số thóc là:
80 + 4 = 84 (tạ)
Xe thứ nhất và xe thứ hai chở được số thóc là:
80 + 84 = 164 ( tạ)
Xe thứ ba chở được số thóc là:
164 : 4 = 41 (tạ)
Cả ba xe chở được tất cả số thóc là:
164 + 41 = 205 ( tạ)
Đáp số: 205 tạ
Câu 37:
Một hình chữ nhật và một hình vuông nằm sát nhau có kích thước như hình A. Tính diện tích toàn bộ hình A.
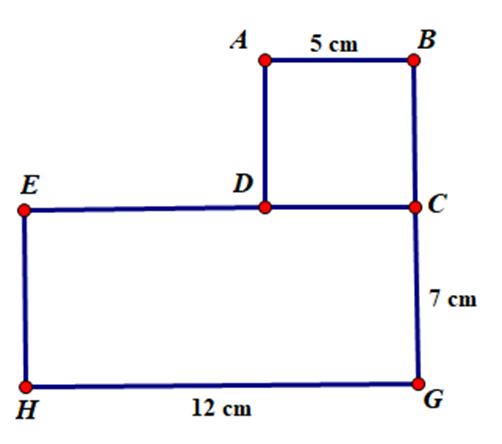
 Xem đáp án
Xem đáp án
Diện tích hình vuông ABCD là:
5 ´ 5 = 25 (cm²)
Diện tích hình chữ nhật ECGH là
7 ´ 12 = 84 (cm²)
Diện tích hình A là:
84 + 25 = 109 (cm²)
Đáp số: 109 cm²
Câu 38:
Một hình chữ nhật và hình vuông nằm sát nhau như hình vẽ. Biết diện tích hình vuông ABCD là 16 cm2. Tính diện tích hình thang DEHG.
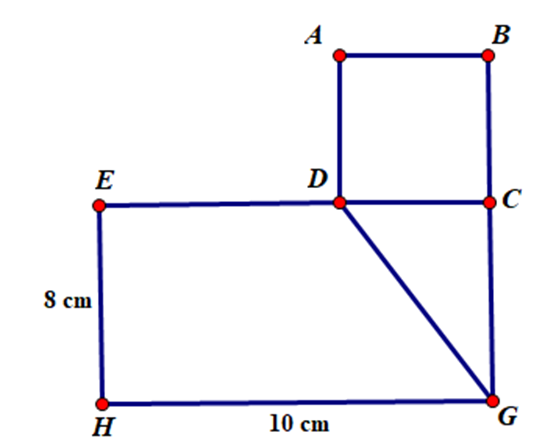
 Xem đáp án
Xem đáp án
Hình vuông ABCD có diện tích = 16 cm2 = 4 ´ 4
Do đó độ dài cạnh CD là 4 cm.
Độ dài cạnh DE là:
10 – 4 = 6 (cm)
Diện tích hình thang DEHG là:
(6 + 10) ´ 8 : 2 = 64 (cm2)
Đáp số: 64 cm2
Câu 39:
Một khu đất hình vuông được quy hoạch thành khu đô thị có diện tích là 360 000 m2. Người ta dựng các cột đèn cao áp theo đường bao quanh của khu đô thị, mỗi cột cách nhau 50 m. Hỏi phải sử dụng bao nhiêu cột đèn cao áp?
 Xem đáp án
Xem đáp án
Ta có:
360 000 = 600 × 600 suy ra độ dài cạnh khu đất hình vuông là 600 m.
Chu vi khu đất hình vuông là:
600 × 4 = 2400 (m)
Cần sử dụng số cột đèn cao áp là:
2400 : 50 = 48 (cột)
Đáp số: 48 cột
Câu 40:
Một mảnh vườn hình chữ nhật đang được tiến hành trồng cây có chiều dài là 28 m. chiều rộng là 12 m2. Người ta trồng các cây cam theo đường bao quanh của mảnh vườn, mỗi cây cách nhau 2 m. Hỏi người ta trồng được bao nhiêu cây cam?
 Xem đáp án
Xem đáp án
Chu vi mảnh vườn hình chữ nhật là:
(28 + 12) × 2 = 80 (m)
Người ta trồng được số cây cam là:
80 : 2 = 40 (cây)
Đáp số: 40 cây
Câu 41:
Một người thợ làm trong 5 ngày được nhận 600 000 đồng tiền công. Hỏi với mức trả công như vậy nếu người thợ làm trong 9 ngày thì được trả bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Tiền công của người thợ đó trong một ngày là:
600 000 : 5 = 120 000 (đồng)
Tiền công của người thợ đó trong 9 ngày là:
120000 × 9 = 1 080 000 (đồng)
Đáp số: 1 080 000 đồng
Câu 42:
Một người thợ làm 24 ngày công trong một tháng được nhận 1 560 000 đồng tiền công. Hỏi trung bình một ngày công người thợ được nhận bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Trung bình 1 ngày công người thợ được nhận số tiền là:
1 560 000 : 24 = 65 000 (đồng)
Đáp số: 65 000 đồng
Câu 43:
Một xí nghiệp dự định may 48 bộ quần áo hết 120 m vải. Ngày đầu máy được 18 bộ, ngày sau may hết 60 m vải. Xí nghiệp còn phải may bao nhiêu bộ quần áo nữa?
 Xem đáp án
Xem đáp án
1 bộ quần áo hết số vải là:
120 : 48 = 2,5 (m )
Ngày sau may được số bộ là:
60 : 2,5 = 24 (bộ)
Xí nghiệp còn phải may số bộ quần áo nữa là:
48 – 18 – 24 = 6 (bộ)
Đáp số: 6 bộ
Câu 44:
Trung bình cộng tuổi của ông, tuổi của bố và tuổi của cháu là 36 tuổi, trung bình cộng tuổi bố và tuổi cháu là 23 tuổi. Ông hơn cháu 54 tuổi. Hỏi tuổi của ông, của bố, của cháu là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng số tuổi của ông, bố và cháu là:
36 × 3 = 108 (tuổi)
Tổng số tuổi của bố và cháu là:
23 × 2 = 46 (tuổi)
Tuổi của ông là:
108 – 46 = 62 (tuổi)
Tuổi của cháu là:
62 – 54 = 8 (tuổi)
Tuổi của bố là:
46 – 8 = 38 (tuổi)
Đáp số: 62 tuổi; 38 tuổi; 8 tuổi
Câu 45:
Tìm hai số biết tổng gấp 9 lần hiệu của chúng và hiệu kém số bé 15 đơn vị
 Xem đáp án
Xem đáp án
Nếu coi hiệu của chúng là 1 phần, còn tổng là 9 phần
Ta có sơ đồ:
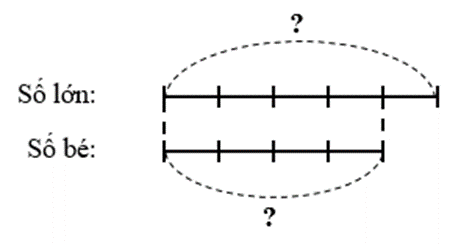
Số bé chiếm số phần là:
(9 – 1) : 2 = 4 (phần)
Số lớn chiếm số phần là:
(9 + 1) : 2 = 5 (phần)
Hiệu kém số bé số phần là:
4 – 1 = 3 (phần)
Giá trị 1 phần là:
15 : 3 = 5
Số lớn là:
5 × 5 = 25
Số bé là:
5 × 4 = 20
Đáp số: 20; 25Câu 46:
Tổng số tuổi hiện nay của hai mẹ con là 36 tuổi. Tuổi con bằng \[\frac{2}{7}\] tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
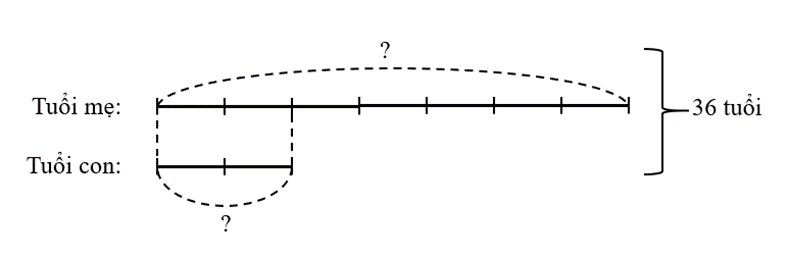
Tổng số phần bằng nhau là:
2 + 7 = 9 (phần)
Tuổi của con hiện nay là:
36 : 9 × 2 = 8 ( tuổi)
Tuổi của mẹ hiện nay là:
36 – 8 = 28 (tuổi)
Đáp số: 8 tuổi; 28 tuổi
Câu 47:
Vụ lúa hè mùa thu nhà Quân thu hoạch được 2 tấn 350 kg thóc. Vụ lúa đông xuân thu hoạch được 2 tấn 650 kg thóc. Cứ 1 tấn thóc bán được 7 400 000 đồng. Hỏi cả 2 vụ lúa nhà Quân sẽ bán được bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Đổi : 2 tấn 350 kg = 2,35 tấn
2 tấn 650 kg = 2,65 tấn
Cả 2 vụ thu hoạch được số thóc là:
2,35 + 2,65 = 5 (tấn)
Cả hai vụ lúa nhà Quân sẽ bán được :
7 400 000 × 5 = 37 000 000 (đồng)
Đáp số: 37 000 000 đồng
Câu 48:
Một người thợ may ngày thứ nhất may được 10 bộ quần áo. Ngày thứ 2 may được nhiều hơn ngày thứ nhất 5 bộ. Hỏi cả hai ngày người đó may được bao nhiêu bộ quần áo?
 Xem đáp án
Xem đáp án
Ngày thứ hai may được số bộ quần áo là:
10 + 5 = 15 (bộ)
Cả hai ngày người đó may được số bộ quần áo là:
10 + 15 = 25 (bộ)
Đáp số: 25 bộ
Câu 49:
Để làm xong một công việc cần 15 người làm trong 8 giờ. Hỏi muốn hoàn thành công việc đó trong 5 giờ thì cần bao nhiêu người?
 Xem đáp án
Xem đáp án
Một người làm xong công việc thì cần số giờ làm là:
15 × 8 = 120 (giờ)
Muốn hoàn thành công việc trong 5 giờ thì cần số người là:
120 : 5 = 24 (người)
Đáp số : 24 người
Câu 50:
Để làm xong một công việc trong 5 giờ cần 12 công nhân. Nếu số công nhân tăng thêm 8 người thì thời gian hoàn thành công việc giảm được mấy giờ ? (Giả sử năng suất làm việc của mỗi công nhân là như nhau)
 Xem đáp án
Xem đáp án
Số công nhân sau khi được tăng thêm là:
12 + 8 = 20 (công nhân)
Một công nhân làm xong công việc thì cần số giờ làm là:
12 × 5 = 60 (giờ)
Nếu 20 công nhân làm thì thời gian hoàn thành là:
60 : 20 = 3 (giờ)
Thời gian hoàn thành công việc giảm số giờ là:
5 – 3 = 2 (giờ)
Vậy thời gian hoàn thành công việc giảm được 2 giờ.
Câu 51:
Cho hình thoi ABCD, đường cao BH = 3 cm với H thuộc AD. Điểm M nằm trong hình thoi có tổng các khoảng cách đến AB và AD là 3 cm. Chứng minh B, M, D thẳng hàng.
 Xem đáp án
Xem đáp án
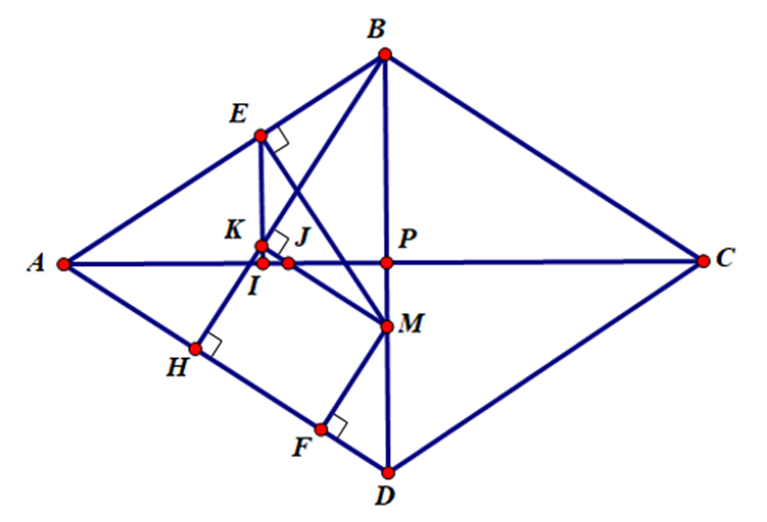
Kẻ ME ^ AB, MF ^ AD, MK ^ BH
Tứ giác HKMF có:
\[\widehat {KHF} = \widehat {HFM} = \widehat {HKM} = 90^\circ \]
Þ HKMF là hình chữ nhật nên HK = MF.
Theo đề bài:
ME + MF = 3 cm
BK + KH = BH = 3 cm
Þ BK = ME
Ta có:
\[\widehat {ABM} = \widehat {ADB}\] (vì ABCD là hình thoi)
MK // AD (vì cùng vuông góc với BH)
Þ \[\widehat {BMK} = \widehat {ADB}\] (hai góc đồng vị)
Þ \[\widehat {BMK} = \widehat {ABM}\](vì cùng bằng \[\widehat {ADB}\])
Xét ΔKBM và ΔEMB có:
BK = ME
\[\widehat {BMK} = \widehat {ABM}\]
\[\widehat {BKM} = \widehat {BEM} = 90^\circ \]
Þ ΔKBM = ΔEMB (cạnh góc vuông – góc nhọn)
\[ \Rightarrow \widehat {KBM} = \widehat {EMB}\]
Gọi O là giao điểm của KB và ME
Þ ΔOMB cân
Þ OM = OB
Mà ME = BK
Þ ME – OM = BK – OB
Þ OE = OK
\[ \Rightarrow \frac{{OE}}{{OM}} = \frac{{OK}}{{OB}}\]
Þ EK // BM (định lý Ta-let) (1)
Gọi EK cắt AC tại I, KM cắt AC tại J, AC cắt BD tại P
Xét ΔIKJ và ΔPMJ có:
\[\widehat {IKJ} = \widehat {JMP}\]
\[\widehat {IJK} = \widehat {MJP}\] (vì đối đỉnh)
Þ ΔIKJ ᔕ ΔPMJ (g.g)
\[ \Rightarrow \widehat I = \widehat P = 90^\circ \]
Þ EK ^ AC. Mà BD ^ AC
Þ EK // BD (2)
Từ (1) và (2) suy ra B, M, D thẳng hàng
Vậy B, M, D thẳng hàng.
Câu 52:
Một bồn hoa hình tam giác. Tổng số đo cạnh thứ nhất và cạnh thứ 2 là \[2\frac{4}{5}\,\,\,m\] . Tổng số đo cạnh thứ 2 và cạnh 3 là \[\frac{{18}}{5}\,\,\,m\]. Tổng số đo của cạnh thứ 3 và cạnh thứ nhất là \[3\frac{2}{{10}}\,\,\,m\]. Tính số đo mỗi cạnh của bồn hoa.
 Xem đáp án
Xem đáp án
Đổi : \[2\frac{4}{5}\,\,\,m = \frac{{14}}{5}\,\,\,m\]
\[3\frac{2}{{10}}\,\,\,m = \frac{{16}}{5}\,\,\,m\]
Tổng số đo độ dài của 3 cạnh là :
\[\left( {\frac{{14}}{5} + \frac{{18}}{5} + \frac{{16}}{5}} \right):2 = \frac{{24}}{5}\,\,\,(m)\]
Số đo của cạnh thứ nhất là :
\[\frac{{24}}{5}\, - \,\frac{{18}}{5} = \frac{6}{5}\,\,\,\,(m)\]
Số đo của cạnh thứ hai là :
\[\frac{{14}}{5}\, - \,\frac{6}{5} = \frac{8}{5}\,\,\,\,(m)\]
Số đo của cạnh thứ ba là :
\[\frac{{24}}{5}\, - \,\frac{{14}}{5} = 2\,\,\,\,(m)\]
Đáp số: \[\frac{6}{5}\,\,\,m\]; \[\frac{8}{5}\,\,\,m\]; 2 m
Câu 53:
Một hộp bánh hình chữ nhật có chiều dài là \[3\frac{3}{5}\,\,\,cm\]. Chiều rộng ít hơn chiều dài \[1\frac{3}{5}\,\,\,cm\]. Tính chu vi hộp bánh đó.
 Xem đáp án
Xem đáp án
Đổi \[3\frac{3}{5}\,\,\,cm = \frac{{18}}{5}\,\,\,cm\]
\[1\frac{3}{5}\,\,\,cm = \frac{8}{5}\,\,\,cm\]
Chiều rộng hộp bánh hình chữ nhật là:
\[\frac{{18}}{5}\,\, - \frac{7}{5} = \frac{{11}}{5}\,\,\,(cm)\]
Chu vi hộp bánh hình chữ nhật là:
\[\left( {\frac{{18}}{5}\,\, + \frac{{11}}{5}\,} \right) \times 2 = \frac{{58}}{5}\,\,(cm)\]
Đáp số: \[\frac{{58}}{5}\,\,cm\]
Câu 54:
Cho tam giác ABC cân tại A. Hai đường trung tuyến BD và CE cắt nhau tại G. Gọi M, N lần lượt là trung điểm của BG và CG. I và K lần lượt là trung điểm của GM, GN. Chứng minh IK // DE.
 Xem đáp án
Xem đáp án
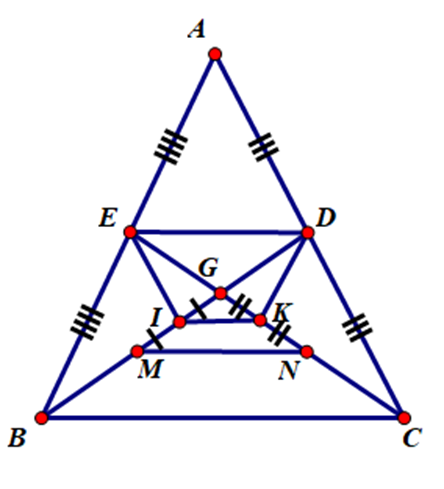
Xét tam giác GBC có:
MG = MB (vì M là trung điểm của GB)
NG = NC (vì N là trung điểm của GC)
⇒ MN // BC (tính chất đường trung bình trong tam giác) (1)
Xét tam giác ABC có:
EA = EB (vì CE là đường trung tuyến ứng với cạnh AB)
DA = DC (vì BD là đường trung tuyến ứng với cạnh AC)
⇒ DE // BC (tính chất đường trung bình trong tam giác) (2)
Từ (1) và (2) ta có MN // DE (3)
Xét tam giác GMN có:
IG = IM (vì I là trung điểm của GM
KG = KN (vì K là trung điểm của GN)
⇒ IK // MN (tính chất đường trung bình trong tam giác) (4)
Từ (3) và (4) ta có IK // DE
Vậy IK // DE.
Câu 55:
Cho tam giác ABC cân tại A. Hai đường trung tuyến BD và CE cắt nhau tại G. Gọi M, N lần lượt là trung điểm của BG và CG. I và K lần lượt là trung điểm của GM, GN. Cho BC = 10 cm. Tính DE + IK.
 Xem đáp án
Xem đáp án
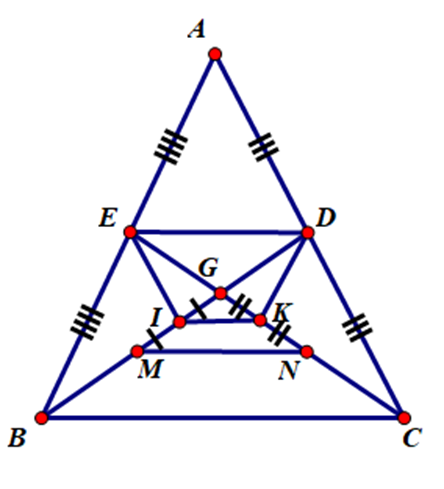
Xét tam giác ABC có:
EA = EB (vì CE là đường trung tuyến ứng với cạnh AB)
DA = DC (vì BD là đường trung tuyến ứng với cạnh AC)
⇒ DE // BC và \[DE = \frac{1}{2}BC\] (tính chất đường trung bình trong tam giác)
Xét tam giác GBC có:
MG = MB (vì M là trung điểm của GB)
NG = NC (vì N là trung điểm của GC)
⇒ MN // BC và \[MN = \frac{1}{2}BC\] (tính chất đường trung bình trong tam giác)
Xét tam giác GMN có:
IG = IM (vì I là trung điểm của GM
KG = KN (vì K là trung điểm của GN)
⇒ IK // MN và \[IK = \frac{1}{2}MN = \frac{1}{4}BC\] (tính chất đường trung bình trong tam giác)
\[ \Rightarrow DE + IK = \frac{1}{2}BC + \frac{1}{4}BC = \frac{3}{4}BC = \frac{3}{4} \cdot 10 = 7,5\,\,cm\]
Vậy DE + IK = 7,5 cm.
Câu 56:
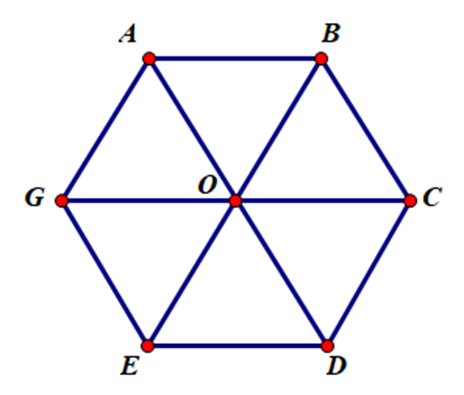
Cho lục giác đều ABCDEG, ba đường chéo chính cắt nhau tại O. Có bao nhiêu hình thoi được tạo thành?
 Xem đáp án
Xem đáp án
Các hình thoi được tạo thành là: AOCB; BODC; ABOG; COED; DOGE; AOEG
Vậy có 6 hình thoi được tạo thành.
Câu 57:
Hai bể nước chứa tất cả 8000 lít nước. Nếu ta tháo bớt 750 lít nước ở bể thứ nhất và 1250 lít nước ở bể thứ hai thì số nước còn lại của hai bể bằng nhau. Hỏi lúc đầu mỗi bể chứa bao nhiêu lít nước?
 Xem đáp án
Xem đáp án
Khi đã tháo bớt nước thì số nước còn lại trong hai bể là :
8000 – 750 – 1250 = 6000 (lít)
Vì sau khi tháo bớt nước ở 2 bể thì số nước còn lại ở hai bể bằng nhau.
Số nước ở mỗi bể khi đã tháo nước là :
6000 : 2 = 3000 (lít)
Lúc đầu bể 1 có số lít nước là:
3000 + 750 = 3750 (lít)
Lúc đầu bể 2 có số lít nước là:
3000 + 1250 = 4250 (lít)
Đáp số: 3750 lít; 4250 lít
Câu 58:
Hai bể nước chứa tất cả 1400 lít nước. Nếu ta tháo bớt 240 lít nước ở bể thứ nhất và 160 lít nước ở bể thứ hai thì số nước còn lại ở bể thứ nhất nhiều hơn số nước còn lại của bể thứ hai là 200 lít. Hỏi lúc đầu mỗi bể chứa bao nhiêu lít nước?
 Xem đáp án
Xem đáp án
Khi đã tháo bớt nước thì số nước còn lại trong hai bể là :
1400 – 240 – 160 = 1000 (lít)
Ta có sơ đồ:
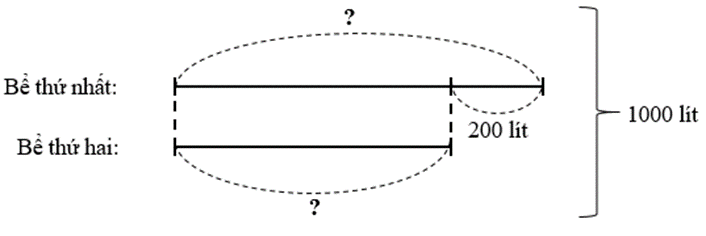
Số nước ở còn lại ở bể thứ nhất là:
(1000 + 200) : 2 = 600 (lít)
Số nước ở còn lại ở bể thứ hai là:
600 – 200 = 400 (lít)
Số nước ban đầu ở bể thứ nhất là:
600 + 240 = 840 (lít)
Số nước ban đầu ở bể thứ hai là:
400 + 160 = 560 (lít)
Đáp số: 840 lít; 560 lít
Câu 59:
Tìm hai số biết tổng của chúng gấp 9 lần hiệu của chúng và hiệu kém số bé 27 đơn vị.
 Xem đáp án
Xem đáp án
Nếu coi hiệu của chúng là 1 phần, còn tổng là 9 phần
Ta có sơ đồ:
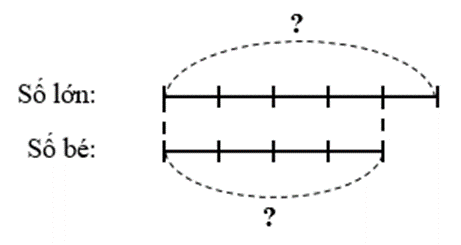
Số bé chiếm số phần là:
(9 – 1) : 2 = 4 (phần)
Số lớn chiếm số phần là:
(9 + 1) : 2 = 5 (phần)
Hiệu kém số bé số phần là:
4 – 1 = 3 (phần)
Giá trị 1 phần là:
27 : 3 = 9
Số lớn là:
5 × 9 = 45
Số bé là:
4 × 9 = 36
Đáp số: 36; 45
Câu 60:
Tìm hai số biết tổng của chúng gấp 3 lần hiệu của chúng và số lớn kém tổng 30 đơn vị.
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
Nếu coi hiệu của chúng là 1 phần, còn tổng là 3 phần
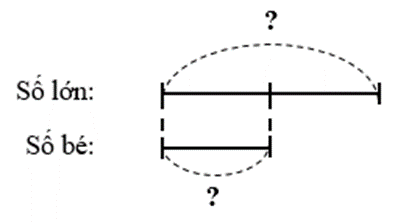
Số bé chiếm số phần là:
(3 – 1) : 2 = 1 (phần)
Số lớn chiếm số phần là:
(3 + 1) : 2 = 2 (phần)
Số lớn kém tổng số phần là:
3 – 2 = 1 (phần)
Giá trị 1 phần là:
30 : 1 = 30
Số lớn là:
30 × 2 = 60
Số bé là:
30 × 1 = 30
Đáp số: 30; 60
Câu 61:
Cho phân số có tổng tử số và mẫu số bằng 136. Tìm phân số đó, biết rằng phân số đó có thể rút gọn thành \[\frac{3}{5} \cdot \]
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
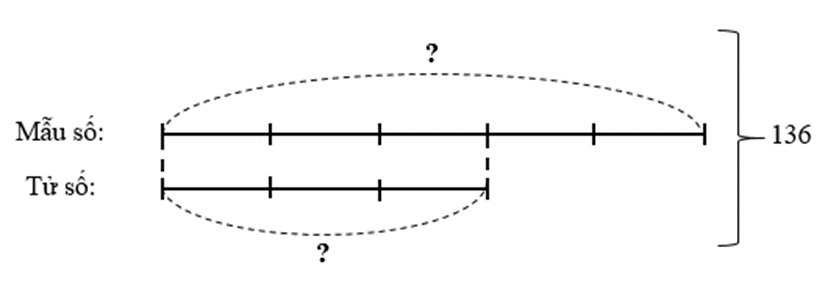
Mẫu số là:
136 : (3 + 5) × 5 = 85
Tử số là:
136 – 85 = 51
Phân số đó là: \[\frac{{51}}{{85}}\]
Đáp số: \[\frac{{51}}{{85}}\]
Câu 62:
Tìm phân số tối giản lớn nhất có tổng của tử số và mẫu số bằng 100.
 Xem đáp án
Xem đáp án
Ta có:
100 = 99 + 1 = 98 + 2 = 97 + 3 = ….
Phân số tối giản lớn nhất có tổng của tử số và mẫu số bằng 100 là: \[\frac{{97}}{3} \cdot \]
Câu 63:
Một chiếc cân bàn dùng để cân các con vật có khối lượng từ 50kg đến 100kg. Ba bạn An, Linh, Nga muốn biết hiện nay mình cân nặng bao nhiêu.Các bạn nhớ rằng lần khấm sức khỏe gần đây, cả ba bạn đều có cân nặng khoảng từ 35 kg đến 40 kg. Em hãy nêu cách để biết được chính xác cân nặng từng bạn khi dùng chiếc cân bàn này?
 Xem đáp án
Xem đáp án
Cách để biết được chính xác cân nặng từng bạn khi dùng chiếc cân bàn này:
Lần 1 : Tính số cân nặng của bạn An và bạn Linh
Lần 2 : Tính số cân nặng của bạn An và bạn Nga
Lần 3 : Tính số cân nặng của bạn Linh và bạn Nga
Tính tổng cân nặng của các lần rồi lấy tổng số cân nặng của 3 bạn đó trừ đi số cân nặng của mỗi lần. Ta sẽ tính được cân nặng của từng bạn.
Câu 64:
Một cửa hàng xăng dầu trong 3 ngày đầu tuần bán được 1150 lít xăng, 4 ngày còn lại trong tuần bán được 3540 lít xăng. Hỏi trung bình mỗi ngày trong tuần đó cửa hàng bán được bao nhiêu lít xăng?
 Xem đáp án
Xem đáp án
Tổng số lít xăng dầu bán được trong tuần là:
1150 + 3540 = 4690 (lít)
Tổng số ngày trong tuần là:
3 + 4 = 7 (ngày)
Trung bình mỗi ngày trong tuần cửa hàng bán được số lít xăng là:
4690 : 7 = 670 (lít)
Đáp số: 670 lít xăng
Câu 65:
 Xem đáp án
Xem đáp án
Tổng số bó hoa bán được trong 3 tuần là:
40 + 32 + 36 = 108 (bó)
Trung bình mỗi tuần cửa hàng bán được số bó hoa là:
108 ÷ 3 = 36 (bó)
Đáp số: 36 bó hoa
Câu 66:
Trung bình cộng của số thứ nhất và số thứ hai là 39. Trung bình cộng của số thứ hai và số thứ ba là 30. Trung bình cộng của số thứ nhất và số thứ ba là 36. Tìm ba số đó?
 Xem đáp án
Xem đáp án
Tổng số thứ nhất và số thứ hai là:
39 × 2 = 78
Tổng số thứ hai và số thứ ba là:
30 × 2 = 60
Tổng số thứ nhất và số thứ ba là:
36 ×2 = 7
Hai lần tổng của ba số là:
78 + 60 + 72 = 210
Tổng của ba số là:
210 : 2 = 105
Số thứ nhất là:
105 – 60 = 45
Số thứ hai là:
105 – 72 = 33
Số thứ ba là:
105 – 78 = 27
Đáp số: 45; 33 và 27
Câu 67:
Trung bình cộng của 3 số là 45. Trung bình cộng của số thứ nhất và số thứ hai là 34. Tìm số thứ ba.
 Xem đáp án
Xem đáp án
Tổng của 3 số là :
45 × 3 = 135
Tổng của số thứ nhất và số thứ hai là :
34 × 2 = 68
Số thứ ba là :
135 - 68 = 67
Đáp số: 67
Câu 68:
Can thứ nhất đựng 12 lít nước. Can thứ hai đựng 16 lít nước. Hỏi can thứ ba đựng bao nhiêu lít nước ? Biết trung bình cộng mỗi can đựng 15 lít nước.
 Xem đáp án
Xem đáp án
Tổng số lít nước của ba can là:
15 × 3 = 45 (lít)
Tổng số lít nước của can thứ nhất và can thứ hai là:
12 + 16 = 28 (lít)
Can thứ ba đựng số lít nước là:
45 – 28 = 17 (lít)
Đáp số: 17 lít
Câu 69:
Thùng thứ nhất đựng 18 lít dầu, thùng thứ hai đựng nhiều hơn thùng thứ nhất 6 lít dầu. Thùng thứ 3 đựng ít hơn thùng thứ nhất 3 lít dầu. Hỏi trung bình mỗi thùng đựng bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Thùng thứ hai đựng số lít dầu là:
18 + 6 = 24 (lít)
Thùng thứ ba đựng số lít dầu là:
18 – 3 = 15 (lít)
Trung bình mỗi thùng đựng số lít dầu là:
(18 + 24 + 15) : 3 = 19 (lít)
Đáp số: 19 lít
Câu 70:
Một vườn hoa hình thoi có tổng độ dài hai đường chéo là 140 m. Đường chéo bé bằng \[\frac{2}{3}\] đường chéo lớn. Người ta sử dụng \[\frac{1}{4}\] diện tích vườn hoa để trồng rau. Tính diện tích phần vườn để trồng rau.
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
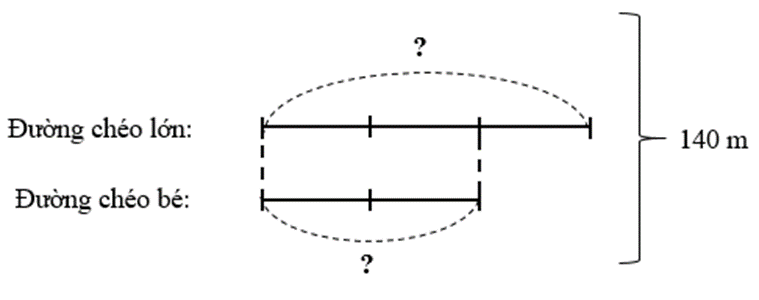
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Độ dài đường chéo bé là:
140 : 5 × 2 = 56 (m)
Độ dài đường chéo lớn là:
140 – 56 = 84 (m)
Diện tích mảnh vườn là:
84 × 56 : 2 = 2352 (m2)
Diện tích đất trồng rau là:
\[2352 \times \frac{1}{4} = 588\,\,\,({m^2})\]
Đáp số: 588 m2
Câu 71:
Một mảnh vườn hình thoi có tổng độ dài hai đường chéo là 220 m, biết đường chéo thứ nhất bằng \[\frac{2}{3}\] độ dài đường chéo thứ hai. Tính diện tích mảnh vườn đó.
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
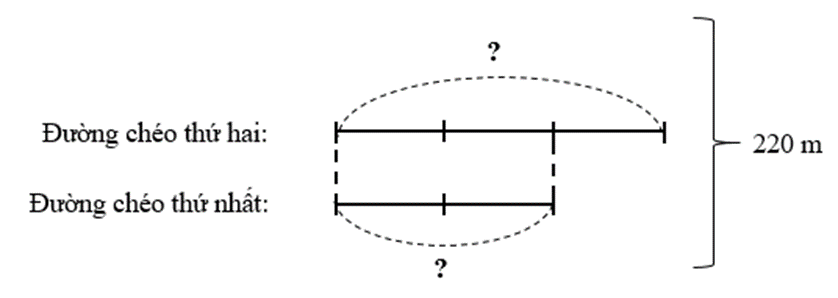
Độ dài đường chéo thứ hai là:
220 : (2 + 3) × 3 = 132 (m)
Độ dài đường chéo thứ nhất là:
220 – 132 = 88(m)
Diện tích mảnh vườn là:
132 × 88 : 2 = 5808 (m2)
Đáp số: 5808 m2
Câu 72:
Trại chăn nuôi nhà bác Hùng tháng thứ nhất bán được 6 tạ gà, tháng thứ hai bán được 3 tạ gà, tháng thứ ba bán được 9 tạ gà. Tháng thứ tư bán được số gà nhiều hơn mức trung bình của 3 tháng đầu là 2 tạ. Hỏi tháng thứ tư bán được bao nhiêu tạ gà?
 Xem đáp án
Xem đáp án
Trung bình của 3 tháng đầu bác Hùng bán được số tạ gà là:
(6 + 3 + 9) : 3 = 6 (tạ)
Tháng thứ tư bán được số tạ gà là:
6 + 2 = 8 (tạ)
Đáp số: 8 tạ
Câu 73:
Một xưởng sản xuất ngày thứ nhất làm được 12 sản phẩm. Ngày thứ hai làm được nhiều hơn ngày thứ nhất 6 sản phẩm. Ngày thứ 3 làm được nhiều hơn ngày thứ hai 6 sản phẩm. Ngày thứ tư làm được bằng \[\frac{2}{3}\] lần trung bình 3 ngày đầu. Hỏi ngày thứ tư làm được bao nhiêu sản phẩm?
 Xem đáp án
Xem đáp án
Ngày thứ hai làm được số sản phẩm là:
12 + 6 = 18 (sản phẩm)
Ngày thứ ba làm được số sản phẩm là:
18 + 6 = 24 (sản phẩm)
Trung bình 3 ngày đầu làm được số sản phẩm là:
(12 + 18 + 24) : 3 = 18 (sản phẩm)
Ngày thứ tư làm được số sản phẩm là:
\[18 \times \frac{2}{3} = 12\](sản phẩm)
Đáp số: 12 sản phẩm
Câu 74:
 Xem đáp án
Xem đáp án
Để sửa xong quãng đường đó trong 1 ngày thì cần số người là:
25 ´ 9 = 225 (người )
Muốn sửa xong quãng đường đó trong 5 ngày thì cần số người là:
225 : 5 = 45 (người )
Đáp số: 45 người
Câu 75:
Một đội công nhân có 63 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa? (Mức làm của mỗi người như nhau).
 Xem đáp án
Xem đáp án
Muốn sửa xong quãng đường trong 1 ngày cần số người là:
63 × 11 = 693 (người)
Muốn sửa xong quãng đưòng trong 7 ngày cần số người là:
693 : 7 = 99 (người)
Số người cần thêm là:
99 – 63 = 36 (người)
Đáp số: 36 người
Câu 76:
Một đội 15 công nhân dự định lắp một cái máy trong 20 ngày, mỗi ngày làm việc 8 giờ. Nếu thêm 5 người nữa mà cả đội làm việc ngày 10 giờ thì lắp cái máy trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Số giờ cần thiết để 15 công nhân lắp máy là:
20 ´ 8 = 160 (giờ)
Thêm 5 người nữa thì đội đó có số công nhân là:
15 + 5 = 20 (người)
Số giờ cần thiết để 20 công nhân lắp xong là:
160 : 20 ´ 15 = 120 (giờ)
Mỗi ngày làm 10 giờ nên số ngày cần làm là:
120 : 10 = 12 (ngày)
Đáp số: 12 ngày
Câu 77:
Một đội 24 công nhân dự định sửa một đoạn đường trong 16 ngày, mỗi ngày làm việc 10 giờ. Do 4 người bị điều chuyển đi sửa đoạn đường khác và cả đội chỉ làm việc mỗi ngày 8 giờ. Hỏi bao lâu đội đó sửa xong đoạn đường?
 Xem đáp án
Xem đáp án
Số giờ cần thiết để 24 công nhân sửa đường xong là:
16 ´ 10 = 160 (giờ)
Giảm đi 4 người nữa thì đội đó có số công nhân là:
24 – 4 = 20 (người)
Số giờ cần thiết để 20 công nhân sửa đường xong là:
160 ´ 24 : 20 = 192 (giờ)
Mỗi ngày làm 8 giờ nên số ngày cần làm là:
192 : 8 = 24 (ngày)
Đáp số: 24 ngày
Câu 78:
 Xem đáp án
Xem đáp án
Số suất ăn dành cho 120 người trong 18 ngày là:
120 ´ 18 = 2160 (suất)
Số người sau khi giảm là:
120 – 80 = 40 (người)
2160 suất ăn đủ cho 40 người ăn trong số ngày là:
2160 : 40 = 54 (ngày)
Đáp số: 54 ngày
Câu 79:
Nhà bếp dự trữ đủ lượng gạo cho 45 người ăn trong 6 ngày. Nếu có 54 người ăn số gạo đó thì số ngày ăn sẽ giảm đi bao nhiêu ngày (biết rằng suất ăn của mỗi người là như nhau).
 Xem đáp án
Xem đáp án
1 người ăn số gạo đó trong số ngày là :
45 ´ 6 = 270 (ngày)
54 người ăn thì số gạo đó ăn trong số ngày là :
270 : 54 = 5 (ngày)
Số ngày giảm đi khi có 54 người ăn là :
6 – 5 = 1 (ngày)
Đáp số : 1 ngày
Câu 80:
Một hộp đựng 10 chiếc thẻ được đánh số từ 0 đến 9. Lấy ngẫu nhiên ra 3 chiếc thẻ, xác suất để 3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5 bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: \[C.\frac{8}{{15}}\]
Gọi A là biến cố "3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5".
Þ \[\overline A \] là biến cố "3 thẻ lấy ra không có thẻ mang chữ số 0 và cũng không có thẻ mang chữ số 5"
Số cách để xảy ra biến cố \[\overline A \] là: \[C_8^3\] (cách)
Số cách để lấy 3 thẻ bất kỳ là: \[C_{10}^3\] (cách)
Xác suất để 3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5 là:
\[P = 1 - \frac{{C_8^3}}{{C_{10}^3}} = \frac{8}{{15}}\]
Vậy đáp án C đúng.
Câu 83:
Một thùng cam có số lượng quả cam trong khoảng từ 200 đến 600. Nếu xếp vào mỗi hộp nhỏ 6 quả, 10 quả, 12 quả hay 14 quả đều vừa đủ. Hỏi trong thùng cam có bao nhiêu quả cam?
 Xem đáp án
Xem đáp án
Gọi số quả cam là x (x Î ℕ*, 200 ≤ x ≤ 600)
Nếu xếp vào mỗi hộp nhỏ 6 quả, 10 quả, 12 quả hay 14 quả đều vừa đủ.
x Î BC(6; 10; 12; 14)
Ta có:
6 = 2.3
10 = 2.5
12 = 22.3
14 = 2.7
Þ BCNN(6; 10; 12; 14) = 22.3.5.7 = 420
Mà x Î BC(6; 10; 12; 14)
Þ x Î {0; 420; 840;…}
Mà 200 ≤ x ≤ 600 Þ x = 420
Vậy số quả cam là 420 quả.
Câu 84:
Một hộp bút có số lượng bút trong khoảng từ 10 đến 90. Nếu chia vào mỗi hộp nhỏ 2 bút, 3 bút, 4 bút hay 5 bút đều vừa đủ. Hỏi trong hộp có bao nhiêu cái bút?
 Xem đáp án
Xem đáp án
Gọi cái bút là x (x Î ℕ*, 10 ≤ x ≤ 90)
Nếu chia vào mỗi hộp nhỏ 2 bút, 3 bút, 4 bút hay 5 bút đều vừa đủ.
x Î BC(2; 3; 4; 5)
Ta có:
2 = 1.2
3 = 1.3
4 = 22
5 = 1.5
Þ BCNN(2; 3; 4; 5) = 1.22.3.5 = 60
Mà x Î BC(2; 3; 4; 5)
Þ x Î {0; 60; 120;…}
Mà 10 ≤ x ≤ 90 Þ x = 60
Vậy hộp có 60 cái bút.
Câu 85:
Trong một đợt lao động, ba khối 7, 8, 9 chuyên chở được 912 m3 đất. Trung bình mỗi học sinh khối 7, 8, 9 theo thứ tự làm được 1,2 m3 ; 1,4 m3 ; 1,6 m3 đất. Số học sinh khối 7; 8 tỉ lệ với 1 và 3. Khối 8 và 9 tỉ lệ với 4 và 5. Tính số học sinh mỗi khối.
 Xem đáp án
Xem đáp án
Gọi số học sinh 3 khối lần lượt là: a, b, c (a, b, c Î ℕ*)
Ta có:
\[\frac{a}{b} = \frac{1}{3} \Rightarrow a = \frac{b}{3} \Rightarrow \frac{a}{4} = \frac{b}{{12}}\]
\[\frac{b}{c} = \frac{4}{5} \Rightarrow \frac{b}{4} = \frac{c}{5} \Rightarrow \frac{b}{{12}} = \frac{c}{{15}}\]
\[ \Rightarrow \frac{a}{4} = \frac{b}{{12}} = \frac{c}{{15}} = x\,\,(x \in {\mathbb{Z}^ + })\]
Þ a = 4x; b = 12x; c = 15x
Mà trung bình mỗi học sinh khối 7, 8, 9 theo thứ tự làm được 1,2 m3 ; 1,4 m3 ; 1,6 m3 đất.
Khối 7 chở được số m3 đất là: 1,2a = 1,2. 4x = 4,8x (m3)
Khối 8 chở được số m3 đất là: 1,4b = 1,4. 12x = 16,8x (m3)
Khối 9 chở được số m3 đất là: 1,6c = 1,4. 15x = 24x (m3)
Ta có: 4,8x + 16,8x + 24x = 912
Þ 45,6x = 912
Þ x = 20
Do đó a = 80; b = 240; c = 300
Vậy số học sinh khối 7; 8; 9 lần lượt là 80; 240; 300 học sinh.
Câu 86:
Trong một đợt trồng cây, ba đội trồng được 65 cây. Trung bình mỗi người của đội 1, 2, 3 đều trồng được 2 cây. Số người đội 1 và 2 tỉ lệ với 2 và 5. Khối 8 và 9 tỉ lệ với 5 và 6. Tính số người mỗi đội.
 Xem đáp án
Xem đáp án
Gọi số người 3 đội lần lượt là: a, b, c (a, b, c Î ℕ*)
Ta có:
\[\frac{a}{b} = \frac{2}{5} \Rightarrow \frac{a}{2} = \frac{b}{5} \Rightarrow \frac{a}{{10}} = \frac{b}{{25}}\]
\[\frac{b}{c} = \frac{5}{6} \Rightarrow \frac{b}{5} = \frac{c}{6} \Rightarrow \frac{b}{{25}} = \frac{c}{{30}}\]
\[ \Rightarrow \frac{a}{{10}} = \frac{b}{{25}} = \frac{c}{{30}} = \frac{{a + b + c}}{{10 + 25 + 30}} = \frac{{2(a + b + c)}}{{2(10 + 25 + 30)}} = \frac{{130}}{{130}} = 1\]
Mà trung bình mỗi người của đội 1, 2, 3 đều trồng được 2 cây.
Đội 1 trồng được số cây là: 2a (cây)
Đội 2 trồng được số cây là: 2b (cây)
Đội 3 trồng được số cây là: 2c (cây)
Ta có: 2a + 2b + 2c = 130
Hay 2(a + b + c) = 130
\[ \Rightarrow \frac{a}{{10}} = \frac{b}{{25}} = \frac{c}{{30}} = \frac{{a + b + c}}{{10 + 25 + 30}} = \frac{{2(a + b + c)}}{{2(10 + 25 + 30)}} = \frac{{130}}{{130}} = 1\]
Þ a = 10; b = 25; c = 30
Vậy số người đội 1, 2, 3 lần lượt là 10; 25; 30 người.