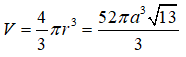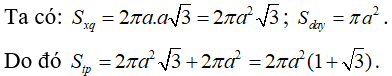20 câu hỏi trắc nghiệm thuộc 20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 (có đáp án)

Câu 1:

Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao $a \sqrt{3}$ $\sqrt{3}$

A. $2 π a^{2} (\sqrt{3} - 1)$

B. $2 π a^{2} \sqrt{3}$

C. $π a^{2} (\sqrt{3} + 1)$

D. $2 π a^{2} (\sqrt{3} + 1)$

Xem đáp án

Đáp án D

Câu 2:

Hình trụ (H) có diện tích xung quanh là 6π(c $m^{2}$ ) và thể tích khối trụ là 9π(c $m^{3}$ ). Chiều cao của hình lăng trụ là:

A. 1 (cm)

B. 3 (cm)

C. $\frac{1}{2}$ (cm)

D. 2 (cm)

Xem đáp án

Đáp án A

Từ giả thiết ta có:

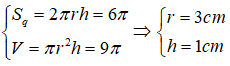
Câu 3:

Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là:

A. $\sqrt{119}$ (cm)

B. 17 (cm)

C. 15 (cm)

D. 13 (cm)

Xem đáp án

Đáp án D

Từ giả thiết ta có:

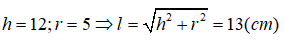
Câu 4:

Một hình nón có đường kính đáy là $2 a \sqrt{3}$ $\sqrt{3}$ , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.

A. $3 π a^{3}$

B. $π a^{3}$

C. $2 \sqrt{3} π a^{3}$

D. $\sqrt{3} π a^{3}$

Xem đáp án

Đáp án B

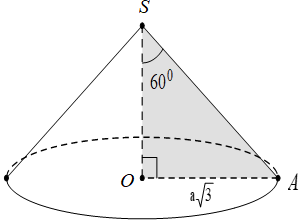
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính

Câu 5:

Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng $a \sqrt{2}$ $\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh $S_{xq}$ của hình nón và thể tích V của khối nón tương ứng là:

A. $S x q = π a^{2}; V = \frac{π a^{3} \sqrt{6}}{12}$

B. $S x q = \frac{π a^{2}}{2}; V = \frac{π a^{3} \sqrt{3}}{12}$

C. $S x q = π a^{2} \sqrt{2}; V = \frac{π a^{3} \sqrt{6}}{4}$

D. $S x q = π a^{2}; V = \frac{π a^{3} \sqrt{6}}{4}$

Xem đáp án

Đáp án A

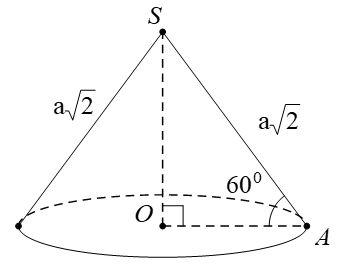
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a $\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy là $\hat{S A O}$ = 60°.

Câu 6:

Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình chữ nhật có diện tích là 2 $a^{2}$ . Diện tích xung quanh của hình trụ là:

A. $4 π a^{2}$

B. $3 π a^{2}$

C. $2 π a^{2}$

D. $π a^{2}$

Xem đáp án

Đáp án C

Từ giả thiết ta có: $r = a; 2 a . h = 2 a^{2} \Rightarrow h = a \Rightarrow S_{x q} = 2 π r h = 2 π a^{2}$

Câu 7:

Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

A. $48 π (c m^{3})$

B. $24 π (c m^{3})$

C. $72 π (c m^{3})$

D. $18 π (c m^{3})$

Xem đáp án

Đáp án C

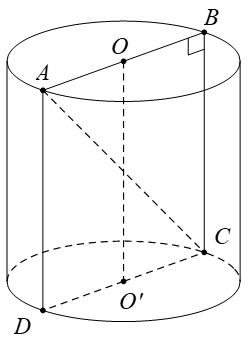
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.

Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là

Câu 8:

Cho khối trụ có diện tích toàn phần là 6π $a^{2}$ và thể tích là 2π $a^{3}$ . Bán kính đáy của hình trụ là:

A. $\frac{3 a}{2}$

B. a

C. $\frac{2 a}{3}$

D. 2a

Xem đáp án

Đáp án B

Từ giả thiết ta có:

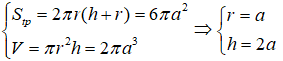
Câu 9:

Tam giác ABC vuông đỉnh A có $\hat{A B C}$ = 60^o và AB = a. Quay miền trong và các cạnh của tam giác ABC quanh trục AB thì ta được khối nón (N). Thể tích của khối nón (N) là:

A. $\frac{π a^{3} \sqrt{3}}{3}$

B. ${πa}^{3}$

C. $3 {πa}^{3}$

D. $\frac{π a^{3}}{3}$

Xem đáp án

Đáp án B

Từ giả thiết ta có: h = AB = a; r = AC = atan60^o = $a \sqrt{3}$

$\Rightarrow V = \frac{1}{3} . π r^{2} h = π a^{3}$

Câu 10:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Thể tích khối nón có đỉnh là tâm O của hình vuông A'B'C'D' và đáy là hình tròn ngoại tiếp hình vuông ABCD là:

A. $\frac{π a^{3}}{3}$

B. πa3πa3

C. $\frac{2 π a^{3}}{3}$

D. $\frac{2 π a^{3} \sqrt{2}}{3}$

Xem đáp án

Đáp án A

Từ giả thiết ta có: h = AA' = 2a;

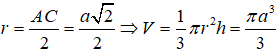
Câu 11:

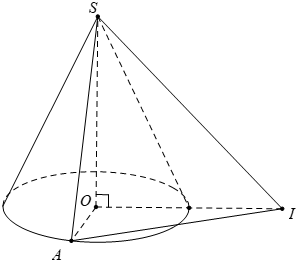
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R $\sqrt{3}$ . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh $S_{xq}$ của hình nón và thể tích V của khối nón là:

A. $S_{x q} = π R^{2} \sqrt{2}; V = \frac{π R^{3}}{3}$

B. $S_{x q} = 2 π R^{2}; V = \frac{2 π R^{3}}{3}$

C. $S_{x q} = \frac{π R^{2} \sqrt{2}}{}; V = \frac{π R^{3}}{6}$

D. $S_{x q} = π R^{2}; V = \frac{2 π R^{3}}{3}$

Xem đáp án

Đáp án A

Câu 12:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy và SA = 2a. Góc giữa cạnh bên SB và đáy là 45^o. Bán kính mặt cầu tâm S và tiếp xúc với BD theo a là:

A. $\frac{a \sqrt{6}}{3}$

B. $\frac{a \sqrt{6}}{6}$

C. $\frac{a \sqrt{6}}{2}$

D. $a \sqrt{6}$

Xem đáp án

Đáp án D

Gọi O là tâm của hình vuông ABCD. Khi đó SO vuông góc với BD. Mặt cầu (S,r) tiếp xúc với BD khi và chỉ khi

r = SO. Từ giả thiết ta có

$\Rightarrow A B = S A = 2 a \Rightarrow A O = a \sqrt{2} \Rightarrow r = S O = a \sqrt{6}$

Câu 13:

Cho hình chóp tứ giác đều S.ABCD có AB = a và góc giữa SA và đáy là 60^o. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) là:

A. $\frac{a \sqrt{42}}{6}$

B. $\frac{a \sqrt{42}}{14}$

C. $\frac{a \sqrt{42}}{7}$

D. $\frac{2 a \sqrt{42}}{7}$

Xem đáp án

Đáp án C

Gọi O là tâm của hình vuông ABCD. Khi đó ta có:

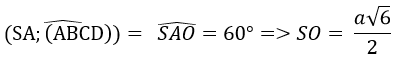
SB = SC = SA = $a \sqrt{2}$

Mặt cầu S(A,r) tiếp xúc với (SBC) khi và chỉ khi

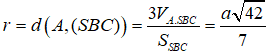
Câu 14:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tạo với mặt phẳng (ABC) một góc là 60^o. Bán kính mặt cầu ngoại tiếp hình chóp là:

A. $a \sqrt{3}$

B. $a \sqrt{2}$

C. $\frac{a \sqrt{3}}{2}$

D. a

Xem đáp án

Đáp án D

Ta có:

Gọi I là trung điểm của SC. Theo định lí ba đường vuông góc ta có tam giác SAC vuông tại A, mà tam giác SBC vuông tại B nên I cách đều các đỉnh của hình chóp hay I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta có bán kính: r = $\frac{S C}{2}$ = a

Câu 15:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = a; AB' = 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là:

A. $5 π a^{2}$

B. $3 π a^{2}$

C. $\frac{5 π a^{2}}{4}$

D. $\frac{5 π a^{2}}{3}$

Xem đáp án

Đáp án A

Ta có mặt cầu ngoại tiếp tứ diện ACB’D’ cũng chính là mặt cầu ngoại tiếp hình hộp chữ nhật nên có bán kính

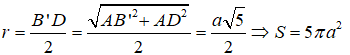
Câu 16:

Cho hình lăng trụ đứng tam giác đều ABC.A'B'C' có AA' = 2AB = 2a. Bán kính của mặt cầu ngoại tiếp hình lăng trụ là:

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{2 a \sqrt{3}}{3}$

C. $\frac{a \sqrt{39}}{3}$

D. $\frac{a \sqrt{7}}{2}$

Xem đáp án

Đáp án B

Gọi O, O’ lần lượt là tâm của các tam giác đều ABC, A’B’C’. Khi đó trung điểm I của OO’ chính là tâm của mặt cầu ngoại tiếp lăng trụ. Bán kính mặt cầu ngoại tiếp lăng trụ là $\frac{2 a \sqrt{3}}{3}$

Câu 17:

Cho hình lăng trụ đứng ABC. $A_{1} B_{1} C_{1}$ có tất cả các cạnh đều bằng nhau và bằng a. Các đáy của lăng trụ nội tiếp các đường tròn đáy của khối trụ (H). Thể tích của khối trụ là:

A. $\frac{π a^{3} \sqrt{3}}{3}$

B. $\frac{π a^{3}}{3}$

C. $\frac{π a^{3}}{9}$

D. $\frac{3 π a^{3}}{4}$

Xem đáp án

Đáp án B

Từ giả thiết ta có đường cao của hình trụ là độ dài cạnh bên của lăng trụ và bán kính đường tròn đáy là bán kính đường tròn ngoại tiếp tam giác ABC nên ta có

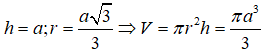
Câu 18:

Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là:

A. $\frac{a \sqrt{7}}{2}$

B. $\frac{a \sqrt{6}}{6}$

C. $\frac{a \sqrt{5}}{6}$

D. $\frac{a \sqrt{15}}{6}$

Xem đáp án

Đáp án D

Gọi H là trung điểm của CD. Khi đó ta có AH ⊥ (BCD), BH ⊥ (ACD). Gọi P, Q lần lượt là tâm của các tam giác đều BCD và ACD. Dựng hình chữ nhật HPIQ thì nó là hình vuông và I là tâm mặt cầu ngoại tiếp tứ diện. Khi đó ta có bán kính mặt cầu là $\frac{a \sqrt{15}}{6}$

Câu 19:

Cho hình chóp tam giác đều S.ABC, mặt phẳng (SBC) tạo với đáy một góc bằng 30^o và SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.ABC là:

A. $\frac{52 π a^{3} \sqrt{13}}{3}$

B. $\frac{4 π a^{3}}{3}$

C. $72 π a^{3} \sqrt{2}$

D. Đáp án khác

Xem đáp án

Đáp án A

Gọi O là tâm của tam giác đều ABC, khi đó SO là đường cao của hình chóp. Gọi M là trung điểm của BC ta có thể suy ra:

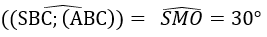
Khi đó ta tính được:

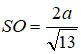
trong mặt phẳng (SAO), trung trực của SA cắt SO tại I thì I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được bán kính của mặt cầu đó là:

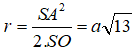
Thể tích khối cầu ngoại tiếp hình chóp là:

Câu 20:

Một cái tháp khổng lồ có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn sơn toàn bộ mặt ngoài của tháp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến mét vuông).

A. S = 8243 ( $m^{2}$ )

B. S = 11762 ( $m^{2}$ )

C. S = 12667 ( $m^{2}$ )

D. S = 23524 ( $m^{2}$ )

Xem đáp án

Đáp án A

CHỌN BỘ SÁCH BẠN MUỐN XEM

20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 (có đáp án)

20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 (có đáp án)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương